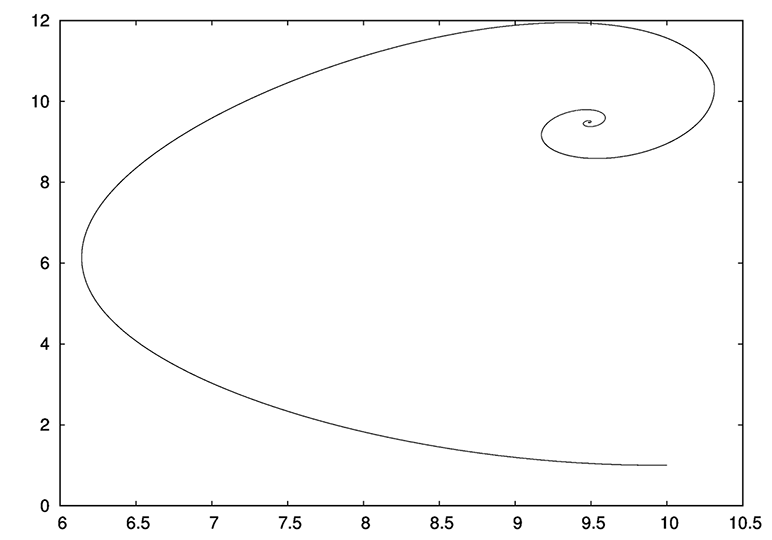
これはHabréの3番目のトピック（ パート1とパート2 ）で、動的なLorentzシステムに専念しています。 私は、このシステムにおける周期的な解（サイクル）の存在の問題を研究し続けています。 パラメータの特定の比率で興味深い結果を得ることができました。
ローレンツ微分方程式系を考えます
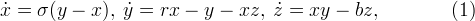
どこで
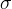、 r 、およびbはいくつかの正の数、システムパラメータです。
そのことを証明しましょう
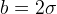、システム（1）には定期的な解はありません（もちろん、平衡位置を除く）。
交換する
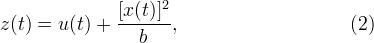
どこで
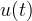-時間の関数。
（2）を区別し、取得します
式（3）の左側で、3番目のシステム方程式（1）の右側を代入し、右側（3）-最初のシステム方程式（1）の右側を代入します。
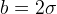。 ゲット
（4）のzの代わりに、式（2）を代入します。
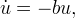
その解は関数です
どこで
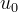任意の定数です。
次に、システムの2番目の方程式（1）で、 zの代わりに式（2）を代入します。 さらに、システムの最初の方程式（1）からyを表します。 ゲット
そして
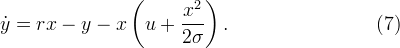
（5）と（6）を（7）に代入すると、
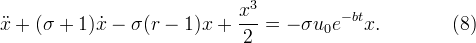
次の場合の非自律的なケースを検討してください。
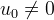式（8）で。 この場合、式（8）に周期Tの周期解があると仮定します。 周期Tの周期関数の導関数は周期Tの周期関数なので、式（8）の左辺は周期Tの周期関数です。 ただし、式（8）の右辺は非周期的です。 
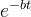周期関数ではありません。 矛盾がありました。
したがって、
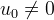式（8）には周期的な解がありません。
ここで、ケースを検討します
。 二次の自律方程式があります
ベンディクソンの基準[1、p。 142-143]定期的な解決策はなく、ローレンツシステムに存在しないことを証明しています。
。
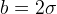この場合、パラメーターrは任意の値を取ることができます。 その後、十分に大きな値では 、パラメーターrは自由対流中の下部と上部の液体層の温度差に比例するため、ローレンツシステムには周期解も存在しません。 層内の温度勾配が大きくなると、流体内に対流軸が現れ、最終的に流体は静止します（層流モード）。 これは、数値実験でも確認されています（トピックの最初に、 r値（軌道アークのxOy平面への投影）の異なる値で安定した焦点が観察されました）。 ほとんどの場合、これは、ローレンツシステムがこのプロセスをかなり大まかに説明しているという事実によって説明されますが、
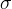b （ rはかなり大きな値をとる）システム（1）では、安定したリミットサイクルが観察されます[2、p。 291-294]。
すべての単純さにもかかわらず、私の意見では、微分方程式の理論の観点からのこの結果は、3次の非線形システムが順序の減少を可能にするという点で興味深いものです。
別の場合を考えます
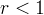。 私に知られている文献では、線形近似で研究されています。 2番目のリアプノフ法を適用します。 リアプノフ関数を構成します
所有プロパティ：
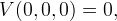
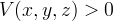のために 
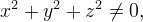
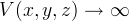で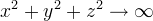 
そして
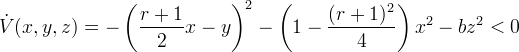のために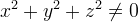 
システムの方程式の右辺によって（1）。 次に、バルバシン・クラソフスキーの定理[3、p。 248-250]任意のシステムソリューション（1）
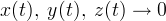で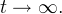 
より一般的なケースは[4]（補題1.2）で説明されており、システム（1）のサイクルが存在しないことが証明されています（レジームの制限-平衡位置）
そして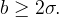 
また、システム（1）には常に次の形式の特定のソリューションがあることに注意してください。
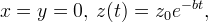
どこで
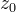任意の定数です。
このトピックでは、システム（1）の定期的な解決策がないという問題を検討しました。 しかし、サイクルの存在に関するシステム（1）のダイナミクスの解析的研究は文献に記載されていますが、多くはローレンツシステムを数値的に研究しているため、多くの情報源はありません。 以下は、パラメータr [2、4–8]の大きな値に対するシステム（1）のリミットサイクルの存在の厳密な証拠を見つけることができた参考文献のリストです。 ヴィクトル・イオシフォヴィッチ・ユドヴィッチ （以前は科学雑誌に未発表）の原稿[4]が含まれており、この問題について詳しく説明しています。
文学
1.ネミツキーVV、ステパノフVV 微分方程式の定性理論。 -M。：URSS社説、2004年。
2. Neymark Yu.I.、Landa P.S. 確率的およびカオス的振動。 -M：LIBROCOM、2009年。
3.デミドビッチB.P. 安定性の数学的理論に関する講義。 -M。：ナウカ、1967。
4.ユドビッチV.I. 大きなレイリー数に対するローレンツシステムのリミットサイクルの漸近式 //原稿の詳細 VINITI、No。2611-78で。 1978。
5.ロビンズKAのロビンズKA 周期解と高Rの分岐構造 // SIAM Journal on Applied Mathematics、36（3）：457-472、1979。
6.清水T.ローレンツモデルの最も単純なリミットサイクルの分析形式//物理学A：統計力学とその応用、97（2）：383-398、1979。DOI： 10.1016 / 0378-4371（79）90113- 4 。
7.ポクロフスキーL.A. 大きなレイリー数の漸近極限におけるローレンツ方程式系の解。 I.最も単純な量子レーザーモデルのローレンツシステム、およびそれへの平均化方法の適用 // Theoretical and Mathematical Physics、62（2）：272-290、1985。
8. Jiming Li、Jianming Zhang。 ローレンツ方程式の高次の周期解とホモクリニック軌道の分岐に関する新しい扱い // SIAM Journal on Applied Mathematics、53（4）：1059-1071、1993。