こんにちは。 この記事では、 非フォン・ノイマンのコンピューター趣味プロジェクトについて説明します。 アーキテクチャは機能的なパラダイムに対応します。プログラムは、互いに基本機能のアプリケーションのツリーです。 鉄は、プログラムの動的ツリーが投影され、計算中にプログラムが「クロール」するプリミティブノードの均一な静的ネットワークです。





これがツリーの仕組みです。ここでは、わかりやすくするために、組み合わせ式ではなく算術式を計算しています。 図のステップはマシンの1ビートです。



これで、初期のプロトタイプの準備が整いました。タクトフリーソフトウェアシミュレーターの形式とFPGAでの実装の形式の両方で存在します。

イデオロギー

従来のアーキテクチャのコンピューターは世界を変えましたが、信じられないほどの、酔わせる成長の期間は明らかに終わりました。 主な制限要因の1つは、並列化を妨げるプロセッサとメモリ間のボトルネックです。 関数型プログラミングは、フォンノイマン集中型アーキテクチャの制限を回避する魅力的な方法ですが、関数型アプローチに基づいてコンピューターアーキテクチャを作成しようとする試みは成功していません 。



しかし、時間が経つにつれて、マイクロエレクトロニクス技術は改善され、より民主的になります。 コンビナトリアルロジックに基づいてコンピューターを作成しようとしています。 計算問題は式として公式化されます-コンビネーター関数の相互のアプリケーションのツリー：

//       (  ) 2+3 = + 2 3 = + ( +1 1 ) ( +1 1 1 ) = + ( +1 1 ) ( +1 +1 1 ) `` ``si`k`s``s`ksk ``s``s`ksk i ``s``s`ksk ``s``s`ksk i
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

プログラムの実行は、この式を、答えを出す簡単な形式に変換することと理解されます。 システムはチューリング完全であり、欠点があります。すべての式を計算できるわけではありません。 組み合わせロジックを使用して何かを計算する方法の詳細については、 こちらとこちらをご覧ください。

建築

主なアイデアは、コンビネータを使用できるセルのハードウェアツリーにプログラムツリーを配置することです。

なぜハードウェアツリーなのか？ 実際、プログラムツリーを通常の1次元アドレス空間に投影すると、非ローカルの「長い」接続が必然的に発生します。 ツリー式のフラットレコードの例を次に示します。「（A * B）+（C * D）-E」ここで、「+」は「-」のデータソースですが、式では間隔が空いています。







非交差サブツリーは、独立して同時に計算できるため、自然な並列性が得られます。 共有メモリはありません。データはローカルに保存されます。つまり、「プロセッサ-バス-メモリ」というのどはありません。 サブツリーのコピーを除くすべての操作は高速です。 前の記事で、このような構造のツリーを使用して数値をソートする方法を示しました。

したがって、ある機能から別の機能へのアプリケーションのツリーがあり、



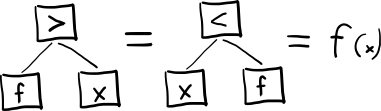
ここで、葉は基本関数です;組み合わせ論理の場合、これらは基本的な組み合わせ、たとえば集合S、K、Iです。

 Ix = Ix = x -   Kxy = (Kx)y = x -   Sxyz = ((Sx)y)z = (xz)(yz) - 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

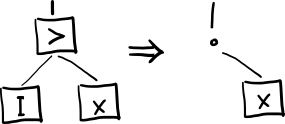
アセンブラーの構文は、難解な関数型プログラミング言語unlambdaから借用されています（ この出版物で最後に約束されているとおり）。

 `ix = Ix ``kxy = (Kx)y ```sxyz = ((Sx)y)z
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このソリューションにより、unlambdaインタープリターを使用して計算の正確性を検証できます。

ここで、プライム（ `）は関数を適用するための記号です。 プレフィックス表記、つまり `fx = f（x）が使用されます。

F（G（X、Y）、H（Z、V））= `` F``GXY``HZV

この形式で式がマシンの入力に送られます。 ダウンロードはツリーのルートを介して行われ、外部デバイスはプログラムキャラクターをルートノードに転送し、最初のキャラクターはそれを取得し、残りをその子孫に渡します。各子孫は再帰的にダウンロード手順を実行します。 サブツリーを完全に受信すると、ノードはこれを祖先に報告し、プログラムの一部の実行を開始します。

作業例

たとえば、ブール式"（1 | 0）＆（0 | 1）"を計算します。 組み合わせベースでは、これは`` `` ssk````siik`ki````sii`kikとして表すことができますはい、そのような表現は読むことができませんが、 教科書を参照して書くことができます。 この種のプログラムを実行した結果、マシンの状態は元の式から単一のブール値（ 「k」としてエンコードされた「1」または「ki」の形式の値「0」）に進化します。 この特定の式では、正確に「k」が得られます。

計算には116クロックサイクルかかります。 これらのうち、最初の67の測定はプログラムのロードを継続します。 実用性の観点からは、この数値は期待できませんが、最適化の可能性があります。たとえば、より豊富な組み合わせのセットを使用すると、プログラムのサイズと実行時間の両方が削減されます。

シミュレータおよびFPGAバージョン

説明された結果は、ソフトウェアシミュレータで取得されました。 ここで勝つためのソースと実行可能ファイル。 シミュレーターはコンソールアプリケーションであり、インストールは不要です。組み合わせ式はコマンドラインパラメーターとして渡されます。





シミュレータは、verilogに実装されているFPGAバージョンに正確に対応していますが、根本的な違いが1つあります。物理リソースの制限はありません。 つまり、シミュレータには潜在的に無限のツリーがあり、そのツリーはFPGA上で制限されています。 63ノードのツリー、つまり深さ6は16,000のAltera LEを占有します。 計算プロセス中にプログラムが大きくなると、計算は失敗します。 ハードウェアバージョンの唯一の利点は、ハードウェアの基本的な実現可能性を示すことです。



計算に戻ります。 それでは、算術式（2 + 1）を計算しましょう。 これを組み合わせ論理の言語に翻訳するために、教会番号を使用します。 式`` `` si`k`s``s`kski``s``s`sskiを取得します。 意味のある何かを得るために、この式を次のように置き換えます： ``（2 + 1）ki 。 これを計算すると、 `k`k`kiが得られます。文字数kは受信した回答を象徴しています。 計算には124クロックサイクルかかります。 しかし、 「（1 + 2）kiの計算にはすでに243サイクルかかり、 「（3 + 3）kiには 380サイクルあります。 悲しいかな、すべては非常に遅いですが、以下に加速経路の概要を示しました。

与えられた例は、単純で無条件の「崩壊する」表現です;実際には、そのようなタスクは伝統的な機械によって最もよく実行されます。 ただし、完全なチューリングシステムである組み合わせロジックを使用すると、計算の複雑さの問題を解決できます。対応する式は、計算の過程で大きくなる可能性があります。 確かに、このプロパティは制御できない成長のリスクをもたらし、プログラムを終了することさえありませんが、提案されたアーキテクチャはそのようなタスクでのみ利点を示すことができます。 ここの説明では、ループと再帰が表示されますが、それらを整理するための古典的な構造は固定小数点の組み合わせです。



`Yx =` x`Yx = `x`x`Yx =` x`x`x`x ...

Y（x）= x（Y（x））= x（x（x（x（...））））

実際のコンビナトリアルマシンの仮想アプリケーション

論理的結論

上記の2つの簡単な例は、ブール計算が算術よりも興味深いように見えることを示しています。マシンはオブジェクトのサイズに非常に敏感です。 しかし、ブール式の計算自体は有望ではありません。タスクは、シーケンシャルマシンであってもO（1）で実行されます。つまり、プログラムは実行されるよりも長くロードされます。

この「欠如」は、 SATタスクを奪われています。 ここでは、変数で補足されたブール式があり、式が成立するかどうかを判断する必要があります。 これはすでにNP完全な問題です。 変数値の複数のセットを同時にチェックすることで、大幅な加速を実現できます。 私が今注目しているのは、このタイプのタスクです。 シンボリック計算や定理の自動証明など、予測不可能な分岐と大きな数の問題は興味深いものです。

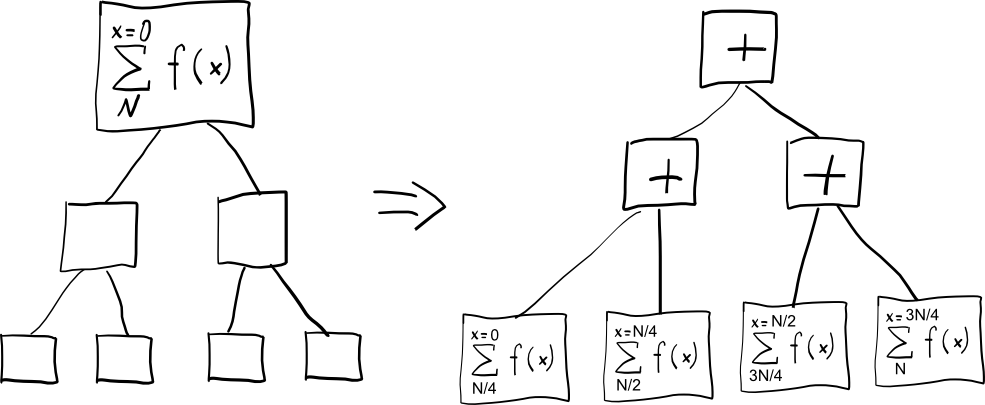
理想的な問題は、最初に種からツリーのように成長し、できるだけ多くの並列ブランチを形成する小さな式で定式化する必要があります。次に、ブランチからの結果を組み合わせて折り返します。

再構成可能なコンピューティング

可能なアプリケーションには、 再構成可能なコンピューティングという別の領域があります。 これは、コンビネーターではないが言語の外部で特別な意味を持つ特別なブロックで機械のアルファベットを補うという考え方です。 コンビナトリアルマシンは2つのフェーズで動作し、最初のフェーズで動作します。 プログラムの実行中に、すべてのコンビネーターを計算する必要があり、（第2フェーズで）ターゲット作業を実行する必要な構造を形成する特別なブロックのみが残ります。



たとえば、論理要素を特別なブロックとして使用する場合、動的FPGAを取得できます。要求に応じて、必要な定数による乗算器、またはパラメーター化された加算回路から計算されたビット深度の加算器など、要求に応じて動的FPGAを形成できます







チェルチェフスキー数（3 + 3）をコンビネータkおよびiに適用したとき、上記とほぼ同じことを行いました。コンビネータは計算プロセスで（関数として）実行されず、結果を視覚化するために使用されました kを単一ビット加算器に置き換えると、計算が完了するまでにビット6の条件付き加算器が得られます。



この潜在的なアプリケーションは、再構成があまり頻繁に必要とされない限り、パフォーマンスをそれほど要求しません。

開発の方向、問題、および可能な解決策

ノードの効率的な使用

機能プログラムツリーは非常にまばらなので、バランスの取れた静的なバイナリツリー上に置くことは非常に不利です。 したがって、近い将来、 セルラーオートマトンの原理で動作する通常のグラフ上に存在するハードウェア動的ツリーへの移行。



しかし、グラフは有限であり、多くの関数式は無限に成長する傾向があります。特に活発な実行の場合はそうです。 これは、今後対処する必要がある別の問題です。 遅延計算ではなくエネルギッシュな計算戦略が使用されているため、おそらく修正する必要がありますが、これを行うには、実用に近いモデルの問題を見つける必要があります。

コマンドシステム拡張

ハードウェアで実装されたコンビネーターのセットを拡張することにより、最適化の面でいくつかの利点を得ることができます。現在、SKIの基本セットを使用します。

 Bxyz = x(yz) -    y Cxyz = xzy - , Wxy = xyy - , Yx = x(Yx) -   . (+1)nfx = f(nfx) -   
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

現時点では入出力はありません。答えは、実行中に変換されたプログラム本体によって与えられます。 IOを実装することは可能ですが、これまでのところ、このタスクは私の優先事項ではありません。



現在、マシンは値渡しのパラメーターを使用しているため、実際にはほとんどの場合、マシンはコピーに従事しているため、引数をコピーする必要があります。 参照による転送を実装するのは魅力的です。ソフトウェアインタープリターにとって、このような移行の効率は桁違いに向上します。 ノードのハードウェアネットワークでこれを実装する方法はまだわかりませんが、おおよその実用的なタスクが表示されたら、真剣にこれを行うつもりです。



マシンの機能を潜在的に拡張するもう1つの機能は、ハードウェアパターンマッチングです。特に、サブツリーの同等性をチェックします。

プログラミングのレベルを改善することも優先度の高いタスクのリストに含まれていますが、すべての努力はシミュレーターの改善に向けられています。

ラムダについて

組み合わせ論理のはるかに成功した姉妹は、ラムダ計算です。 関数型プログラミングのこのオプションの計算ツリーを変更することは可能ですか？ 原則として、はい。 主な迷惑は、変数名が無限にある可能性があることです。つまり、変数呼び出しを1つのハードウェアノード（最終）にスタックすることはできません。 しかし、それは解決可能です。 原則として、より一般的なモデルとしてラムダ計算に切り替えることができます。 コンビネータはサブツリー操作によりエレガントに投影されるため、コンビナトリアルロジックに決めました。

背景

私は、10年前にMIREA大学院で勉強したときに、上司のVadim Nikolayevich Falkから機能プログラムの専門的な計算機を作成するというアイデアを採用しました。 チームの科学的研究は、機能的および機能的論理プログラミングの分野における理論的研究に焦点を合わせました。 特に、Falkは一種の機能的アセンブラーであるFalgol言語を開発しました。 彼は、プログラムの正しさを証明するなど、理論的および計算的な目的のために自分自身を位置づけましたが、それに基づいてコンピューターを構築する試みがありました。



正直に言って、私は少し違うことをして、本当に成功しませんでしたが、機能的な論理コンピューターを作成するというアイデアが植え付けられ、10年後にそれは芽生えました。 この間ずっと、マイクロ回路を含む鉄を開発する会社でシステムプログラマーとして働いていたので、デジタル回路の基礎を習得し、問題をハードウェアプロトタイプに持ち込むことができました。

おわりに

プロジェクトは進行中です。 いくつかの興味深いパラダイムの機能を組み合わせたノイマンコンピューターの背景ではなく、プロトタイプを作成することができました。関数型プログラミング、セルオートマトン。 アナログは私には知られていない。 FPGAオプションは、容量の制限によりほとんど役に立たないが、ハードウェアモデルと完全に一致するソフトウェアシミュレータを使用すると、プログラムの実行を調べることができます。 現在の形式では実用化の話はありませんが、マシンの将来の使用の目標となるモデルタスクを既に探しています。

結論として、電子機器の近代的な開発により、非常に重要なアイデアを実装できるようになりましたが、これは骨の折れる仕事です。 ご清聴ありがとうございました。

参照資料

R. V. Dushkin別名darkus 「コンビネーターは簡単」

デイビッド・マドア「Unlambdaプログラミング言語」

Unlambda言語インタープリター