オプションの基本
オプションの性質と価格設定について簡単に説明します。 オプションには4つの主要なパラメーターがあります。
1. 原資産
2. オプションのタイプ （コールまたはプット）
3. 行使価格（オプション行使価格）
4.オプションの有効期限 （有効期限）
オプションの買い手にとっては 、満期日の行使価格で原資産を購入する（コールオプション）または売却する（プットオプション） 権利を表します。 オプションの売り手にとっては 、満期日の行使価格で原資産を売却（コールオプション）または購入（プットオプション）する義務を表します。 実際、オプションは、取引の時点から有効期限までの原資産（BA）の価格の変動に対する保険です-売り手は保険会社として機能し（BAの価格の不利な変更の場合、オプションの買い手に保険を支払います）、保険契約者はオプションの買い手です（売り手に保険を支払います） ）
保険の価格と同様に、オプションの価格は「被保険者イベント」の確率によって完全に決定されます。 オプションの行使（オプションの買い手の権利の行使）。 この確率とオプション価格、買い手が支払い、売り手が受け取る保険のコストに影響する主な要素：
- 行使価格と原資産の価格の差 。 つまり コールを購入する場合、ストライクが高いほど安くなります（BAが満了時にストライク価格よりも高くなる可能性があるため）
- 基本資産のボラティリティ 。 BAのボラティリティ（おおよそ価格変動の範囲）が高いほど、満了前にストライクに達する可能性が高くなります。
- 有効期限までの時間 。 オプションの有効期限が切れるまでの時間が長いほど、コールの購入時に原資産の価格がストライクを上回る確率が高くなるため、オプション価格は高くなります。
この場合、 これら3つのコンポーネントそれぞれのオプション価格の依存性は非線形です。 これらの重要な要素に対して一般的に受け入れられているオプション価格設定式は、1973年にフィッシャーブラックとマイロンショールズによって開発されました。
Black-Scholesの式の形式は次のとおりです（Wikipediaで詳細を確認できます）。
（ヨーロッパ）コールオプションの価格：
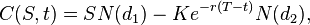
（ヨーロッパ）プットオプションの価格：
指定：
C（S、t） -オプションの有効期限前（有効期限前）の時刻tでの呼び出しオプションの現在の値。
Sは原資産の現在の価格です。
N（x）は、標準正規分布の条件下で偏差が小さくなる確率です（したがって、標準正規分布関数の値の範囲を制限します）。
Kはオプションの行使価格です。
r-リスクフリー金利;
T-t-オプションの有効期限までの時間。
-原資産のボラティリティ（分散の平方根）をもたらします。
ギリシャ人のオプション
BA価格、ボラティリティ、および有効期限に対するオプション価格の感度を評価するために、ギリシャ語と呼ばれる係数が使用されます（係数は、「vegi」を除くギリシャ文字で主に示されます）。
ブラックショールズモデルのギリシャ人は、次のように計算されます。
1. デルタ （
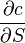）-BA価格の変更からオプション価格が変更されるレート。 呼び出しオプションの場合、デルタは次と等しくなります 
、プットオプション用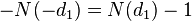 
。 デルタは、BAの価格に応じたオプション値曲線の現在の傾きを示します。
2. ガンマ （
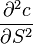）-デルタの変更によるオプション価格の変更率（またはBAの価格の変更による加速）。 ガンマが等しい 
。
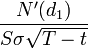3. ベガ （
）-BAのボラティリティの変化に対するオプション価格の依存性を説明します。 
。 Vegaは、ボラティリティの変化の各パーセンテージポイント（1％）で変化するオプション値のポイント数を反映します。
4. シータ （
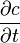）-有効期限が切れるまでの時間に応じたオプション価格の引き下げについて説明します。 通話用- 
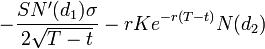、プット用- 
。
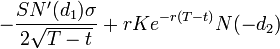上記の式は、ストックオプションの場合を含む一般的な場合に当てはまります。 先物契約のオプションを計算する場合、リスクフリーレートrは適用されません。 なぜなら 先物のオプションはモスクワ証券取引所で取引されているため、計算では金利を考慮していません。
MS Excelでのモデルの実装
そのため、Excel + VBAでのBlack-Scholesモデルの実装。
便宜上、BSモデルの変数ごとに関数を作成します。 各関数には入力変数があります。
S-BA価格
X-行使価格
dは有効期限までの日数です
yは1年の日数
v-ボラティリティ
OptionType-オプションタイプ「Call」または「Put」（価格とデルタの計算専用）
VBAでの通常の関数の記述は次のとおりです。
関数名関数（コンマで区切られた入力変数）
...計算...
FunctionName = ...計算...
終了機能
このような関数は、Excelワークシートからだけでなく、他の関数からも呼び出すことができます。
関数は作成されたモジュールに書き込まれます（たとえば、Alt + F11を押してExcelでVBAを実行し、[挿入]-> [モジュール]を選択します）。
関数d_1（S、X、d、y、v）
T = d / y
d_1 =（Log（S / X）+（0.5 *（v ^ 2））* T）/（v *（T ^ 0.5））
終了機能
関数d_2（S、X、d、y、v）
T = d / y
d_2 = d_1（S、X、d、y、v）-v *（T ^ 0.5）
終了機能
関数Nd_1（S、X、d、y、v）
Nd_1 = Application.NormSDist（d_1（S、X、d、y、v））
終了機能
関数Nd_2（S、X、d、y、v）
Nd_2 = Application.NormSDist（d_2（S、X、d、y、v））
終了機能
関数N_d_1（S、X、d、y、v）
N_d_1 = Application.NormSDist（-d_1（S、X、d、y、v））
終了機能
関数N_d_2（S、X、d、y、v）
N_d_2 = Application.NormSDist（-d_2（S、X、d、y、v））
終了機能
関数N1d_1（S、X、d、y、v）
T = d / y
N1d_1 = 1 /（2 * Application.Pi（））^ 0.5 *（Exp（-0.5 * d_1（S、X、d、y、v）^ 2））
終了機能
関数OptionPrice（OptionType、S、X、d、y、v）
OptionType = "Call"の場合Then
OptionPrice = S * Nd_1（S、X、d、y、v）-X * Nd_2（S、X、d、y、v）
ElseIf OptionType = "Put" Then
OptionPrice = X * N_d_2（S、X、d、y、v）-S * N_d_1（S、X、d、y、v）
終了する場合
終了機能
関数デルタ（OptionType、S、X、d、y、v）
OptionType = "Call"の場合Then
Delta = Application.NormSDist（d_1（S、X、d、y、v））
ElseIf OptionType = "Put" Then
Delta = Application.NormSDist（d_1（S、X、d、y、v））-1
終了する場合
終了機能
関数シータ（S、X、d、y、v）
T = d / y
シータ=-（（S * v * N1d_1（S、X、d、y、v））/（2 *（T ^ 0.5）））/ y
終了機能
関数ガンマ（S、X、d、y、v）
T = d / y
ガンマ= N1d_1（S、X、d、y、v）/（S *（v *（T ^ 0.5）））
終了機能
関数Vega（S、X、d、y、v）
T = d / y
ベガ=（S *（T ^ 0.5）* N1d_1（S、X、d、y、v））/ 100
終了機能
完成したExcelファイルは、 リンクからダウンロードできます。
Excelセルでは、たとえば、セルに= OptionPrice（「Put」; 76870; 90,000; 13; 365; 0.47）と入力することで、指定した関数を呼び出すことができます。原資産の価格76870、ストライク90,000、推定ボラティリティ45有効期限の％および13日前。
私が注意したいいくつかのポイント
- 私たちのプログラムで得られた理論値は、Mosbirzhaによって送信されたものとほぼ同じです。つまり、取引所は計算でBSモデルを使用します。
- 実際、オプション（保険など）には真の公正価値はありません-それはすべての人に固有のものであり、どのようなボラティリティが想定されるか、日数を考慮する方法に依存します（週末、週の異なる日を考慮に入れる重さ、年に何日を考慮するか）式で使用）など
- ギリシャ人には注目すべき特性があります。先物とオプションのポートフォリオでギリシャ人の価値を得るには、ポートフォリオの個々の資産に対応するギリシャ人を追加するだけです。 つまり たとえば、この先物の価格が変わったときにポートフォリオの合計値が変わらないように、基本的な先物の売買額を簡単に計算できます（いわゆるデルタアライメントまたはデルタヘッジ）。
- その普及率にもかかわらず、BSモデルは、資産のリターンが正規の分布を持ち、実際の市場では決して実行されないという仮定に基づいています。
まとめ
そのため、VBAで動作するオプション計算機を入手しました。これは、オプションのプロパティの調査（さまざまな市場パラメーターに対する価格とギリシャの依存関係の図を作成する）と、より複雑なプログラムの取引と構築の両方に使用できます。