🎐 👩🏻‍🎤 🕊️ C ++ 11の可変長テンプレートとコンパイル時の長い演算 👶🏾 🏒 👏🏻

Bell Labsの腸に登場してから30年が経ち、C ++は「高度なC」から最も一般的で表現力豊かなコンパイル済み言語の1つへと大きく進化しました。特に、著者の純粋に個人的な見解では、C ++に新しいC ++ 11標準を与えました。これは、コンパイラのサポートを急速に獲得しています。この記事では、最も強力な機能の1つである「手で触る」ことを試みます-可変数の引数を持つテンプレート （可変長テンプレート ）。

Alexandrescuの本に精通している開発者は、おそらく型リストの概念を覚えているでしょう。古き良きC ++ 03では、必要に応じて、未知の数のテンプレート引数を使用するために、そのようなリストを作成し、それを巧妙なハックで使用することが提案されました。タプル（現在の標準::タプル）などは、この方法で実装されました。などなど。また、型リストの章自体は、関数型スタイルで記述できる場合に限り、C ++テンプレートで（たとえばλ-calculusを実行するために）実際にあらゆる種類の計算を実行できることを明らかにしました。同じ概念を長い算術にも適用できます。長い数値をintのリストとして保存し、フォームのメインクラスを導入します

template<int digit, class Tail> struct BigInteger { };

、彼に対する操作など。しかし、新しい標準の栄光のために、私たちは反対の方向に進みます。

パラメータパック

したがって、基本の基礎はC ++ 11で導入された新しい構文です。最初に、タプルクラスの定義がどのように見えるかを見てみましょう。これは人道に対する犯罪ではありません。

 template<typename... Types> class tuple { // ... };

テンプレート引数の省略記号に注意してください。現在、 Types

は型名ではありませんが、 パラメーターパックはゼロ個以上の任意の型のコレクションです。使い方は？ずるい。

最初の方法：関数またはメソッドの引数タイプのセットとして。これは次のように行われます。

 template<typename... Types> void just_do_nothing_for_no_reason(Types... args) { // indeed }

ここで、 Types... args

は別の特別な構文構造（ function parameter pack ）であり、関数引数チェーンの対応する引数パックに展開されます。 C ++はテンプレート関数の引数の自動検出をサポートしているため、この関数を任意の型の任意の数の引数で呼び出すことができます。

さて、それから何？これらすべての議論で何ができますか？

まず、引数の数が異なる他の関数またはテンプレートのタイプとして、さらにそれをさらに使用できます。

 template<typename... Types> tuple<Types...> make_tuple(Types... args) { tuple<Types...> result(args...); return result; }

Types... args

すでに知っているTypes... args

。 args...

は別の特別な構成（ パラメーターパック拡張 ）です。この場合、コンマで区切られた関数引数のリストに展開されます。そのため、 make_tuple(1, 1.f, '1')

コードのどこかに配置すると、フォームの関数が作成されて呼び出されます

 tuple<int, float, char> make_tuple(int a1, float a2, char a3) { tuple<int, float, char> result(a1, a2, a3); return result; }

第二に、より複雑な変換で使用できます。実際、パラメーターパックの展開では、コンマで区切られたあらゆるものをサポートしています。そのため、次の関数を簡単に実装できます。

 template<typename... Types> std::tuple<Types...> just_double_everything(Types... args) { std::tuple<Types...> result((args * 2)...); // OMG return result; }

IIIii-はい、あなたはそれを推測しました！コンストラクト((args * 2)...)

は(a1 * 2, a2 * 2, a3 * 2)

ます。

最後に、3番目に（そして最も一般的な）、引数リストを再帰で使用できます。

 template<typename T> std::ostream& print(std::ostream& where, const T& what) { return where << what; } template<typename T, typename... Types> std::ostream& print(std::ostream& where, const T& what, const Types& ... other) { return print(where << what << ' ', other...); }

出力はタイプセーフなprintfです-間違いなく価値があります！

一定量のテンプレートマジックの助けを借りて、数からパックからタイプと値を抽出し、他の詐欺を実行する方法を学ぶことができます。ネタバレの下の例。

タプルのリスト

 template<int ...> struct seq { }; //     template<int N, int... S> //     Python' range() struct make_range : make_range<N-1, N-1, S...> { }; template<int ...S> struct make_range<0, S...> { typedef seq<S...> result; }; template<typename... Types, int... range> std::ostream& operator_shl_impl( std::ostream& out, const std::tuple<Types...>& what, const seq<range...> /* a dummy argument */ ) { return print(out, std::get<range>(what)...); } template<typename... Types> std::ostream& operator<<(std::ostream& out, const std::tuple<Types...>& what) { using range = typename make_range<sizeof...(Types)>::result; return operator_shl_impl(out, what, range()); }

ここにはsizeof...(Types)

コマンドがありますが、これはまだ言及されていませんが、理解するのは非常に簡単です-パラメーターパック内の型の数を返します。ところで、それは独立して実装することができます。

だから、行の全体のポイント

 print(out, std::get<range>(what)...);

タプルからの引数を使用して関数を呼び出すだけです。考えてみてください！この焦点のために、0から（n-1）までの数字のリストが必要でした-この行が次のように展開するのは彼のおかげです

 print(out, std::get<0>(what), std::get<1>(what), std::get<2>(what));

（n-1）から0までリストジェネレーターを記述します。1行でタプルを展開できます。

 auto reversed_tuple = std::make_tuple(std::get<rev_range>(my_tuple)...);

道徳：パックの展開はキラーツールです。

長い演算

長い算術の実装を始めましょう。まず、メインクラスを定義します。

 template<uint32_t... digits> struct BigUnsigned { static const size_t length = sizeof...(digits); //   }; using Zero = BigUnsigned< >; using One = BigUnsigned<1>;

C ++のコンパイル段階でのコンピューティングの最高の伝統では、実際、ここのデータはどこにも保存されず、テンプレートの直接の引数です。 C ++は、異なるパラメーターセットを持つBigUnsignedクラスの実装を区別します。これにより、計算を実装できます。最初のパラメーターには長い数値の下位32ビットが含まれ、最後のパラメーターには先頭のゼロを含む可能性のある最上位32ビットが含まれることに同意します（個人的にはこれを最も論理的なソリューションと考えています）。

加算の実装を行う前に、長い数値の連結操作を定義しましょう。この操作を例として使用して、将来使用する標準的な戦術を紹介します。

したがって、2つのタイプで操作を定義します。

 template<class A, class B> struct Concatenate { using Result = void; };

これら2つのタイプはBigUnsigned実装になることを意味します。それらの操作を実現します。

 template<uint32_t... a, uint32_t... b> struct Concatenate<BigUnsigned<a...>, BigUnsigned<b...>> { // >> -    C++11 using Result = BigUnsigned<a..., b...>; // !    ! };

ビットごとの演算を実装することも、ささいなことではありません。たとえば、（非常に単純な）xor：

 template<class A, class B> struct Xor; template<uint32_t... a, uint32_t... b> struct Xor<BigUnsigned<a...>, BigUnsigned<b...>> { using Result = BigUnsigned< (a^b)... >; //  ,     a  b  };

さて、実際に、追加。回避策はありません-再帰を使用する必要があります。メインクラスと再帰ベースを定義します。

 template<class A, class B> struct Sum; template<class A> struct Sum<Zero, A> { using Result = A; }; template<class A> struct Sum< A, Zero> { using Result = A; }; //       ,      : template< > struct Sum<Zero, Zero> { using Result = Zero; };

次に、基本的な計算について説明します。

 template<uint32_t a_0, uint32_t... a_tail, uint32_t b_0, uint32_t... b_tail> struct Sum<BigUnsigned<a_0, a_tail...>, BigUnsigned<b_0, b_tail...>> { static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0; using Result = typename Concatenate< BigUnsigned<a_0 + b_0>, typename Sum< typename Sum< BigUnsigned<a_tail...>, BigUnsigned<b_tail...> >::Result, BigUnsigned<carry> >::Result >::Result; };

それで、何が起こった。

テンプレートを表示

 template<uint32_t a_0, uint32_t... a_tail, uint32_t b_0, uint32_t... b_tail> struct Sum<BigUnsigned<a_0, a_tail...>, BigUnsigned<b_0, b_tail...>> {

長い数字の最下位ビットをすべての上位ビットから分離する必要があります。より一般的なテンプレートを使用した場合

 template<uint32_t a..., uint32_t b...> struct Sum<BigUnsigned<a...>, BigUnsigned<b...>> {

、これを行うのはそれほど簡単ではなく、さらにいくつかの補助構造が必要になります。（しかし、それらを賢明に書いて、その後、唐津の繁殖を実現することは可能です、ニャ！）

次の行

  static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0;

現在のビットでオーバーフローが発生したかどうかを示す、いわゆるキャリービットを計算します。（ UINT32_MAX

定数の代わりに、 std :: numeric_limitsを使用できUINT32_MAX

。使用するUINT32_MAX

がありUINT32_MAX

。）

最後に、最終的な計算は、ルールに従って再帰を使用して結果を見つけます

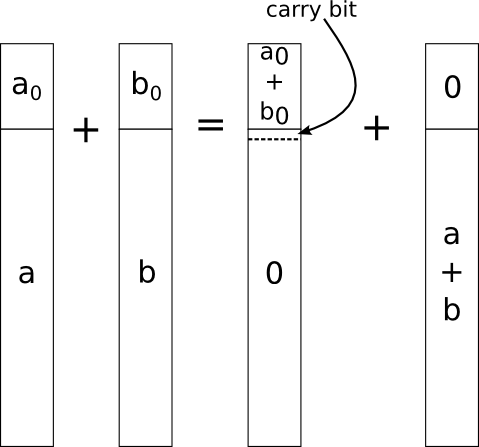
さて、テストできます！実際の計算は次のようになります。

 using A = BigUnsigned<0xFFFFFFFFFFFFFFFFULL>; using B = One; using C = Sum<A, B>::Result; int main(int argc, char** argv) { // ... }

コンパイル済み！ローンチ！しかし... ... Cの意味をどのように知っていますか？実際には、どのように何かをテストするのですか？

簡単な方法：コンパイル段階でエラーをスローしましょう。たとえば、main

 int main(int argc, char** argv) { C::entertain_me(); }

このようなコードをコンパイルしようとすると、論理エラーが発生します。

 static_bignum.cpp:   «int main(int, char**)»: static_bignum.cpp:32:5: : «entertain_me»    «C {aka static_bignum::BigUnsigned<0, 1>}» C::entertain_me(); ^

しかし、このエラーg ++が主な秘密を教えてくれました-Cがstatic_bignum::BigUnsigned<0, 1>

、つまり2 ^32に等しいことがstatic_bignum::BigUnsigned<0, 1>

-すべてが一緒になりました！

それほど簡単ではない方法：与えられた数のバイナリ表現で文字列を生成する関数を書きましょう。空白は次のようになります。

 template<class A> struct BinaryRepresentation; template<uint32_t a_0, uint32_t... a> struct BinaryRepresentation<BigUnsigned<a_0, a...>> { static std::string str(void) { // ... } };

標準のstd :: bitsetオブジェクトを使用して、各段階で現在の32ビットを出力します。

 template<class A> struct BinaryRepresentation; template<uint32_t a_0, uint32_t... a> struct BinaryRepresentation<BigUnsigned<a_0, a...>> { static std::string str(void) { std::bitset<32> bset(a_0); return BinaryRepresentation<BigUnsigned<a...>>::str() + bset.to_string(); } };

再帰ベースを設定するためにのみ残ります：

 template<> struct BinaryRepresentation<Zero> { static std::string str(void) { return "0b"; // Oppa Python Style } };

プリミティブテストの新しいバージョンは次のようになります。

 using A = BigUnsigned<0xFFFFFFFFFFFFFFFFULL>; using B = One; using C = Sum<A, B>::Result; int main(int argc, char** argv) { std::cout << BinaryRepresentation<C>::str() << std::endl; }

そしてその読みやすさで私たちに単に驚くべき答えを与えます

 0b00000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000

ただし、ゼロの数を慎重にカウントすることにより、これがまだ2 ^32であることを確認できます！

複雑ですが、最も説得力のある方法-10進表記の導出-には、いくつかの作業、つまり除算演算の実装が必要になります。

そのためには、一定の前提条件が必要です。

減算実装

 template<class A, class B> struct Difference; struct OverflowError {}; // -  (    ) //     --    : template<> struct Difference<Zero, Zero> { using Result = Zero; }; template<uint32_t n, uint32_t... tail> //   --   struct Difference<BigUnsigned<n, tail...>, Zero> { using Result = BigUnsigned<n, tail...>; }; template<uint32_t n, uint32_t... tail> //    --   struct Difference<Zero, BigUnsigned<n, tail...>> { using Result = OverflowError; }; template<class A> struct Difference<OverflowError, A> { using Result = OverflowError; }; template<class A> struct Difference<A, OverflowError> { using Result = OverflowError; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct Difference<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...> > { using A = BigUnsigned<a_n, a_tail...>; //      using B = BigUnsigned<b_n, b_tail...>; using C = typename Difference<BigUnsigned<a_tail...>, BigUnsigned<b_tail...>>::Result; using Result_T = typename std::conditional< //    ? a_n >= b_n, C, typename Difference<C, One>::Result >::type; using Result = typename std::conditional< //     a_n == b_n && std::is_same<Result_T, Zero>::value, Zero, typename Concatenate< BigUnsigned<a_n - b_n>, Result_T >::Result >::type; };

ビットシフトの実装

メインクラスを定義し、再帰ベースを設定します。

 template<class A, size_t shift> struct ShiftLeft; template<class A, size_t shift> struct ShiftRight; template<class A, size_t shift> struct BigShiftLeft; template<class A, size_t shift> struct BigShiftRight; template<class A, size_t shift> struct SmallShiftLeft; template<class A, size_t shift> struct SmallShiftRight; template<size_t shift> struct BigShiftLeft <Zero, shift> { using Result = Zero; }; template<size_t shift> struct BigShiftRight <Zero, shift> { using Result = Zero; }; template<size_t shift> struct SmallShiftLeft <Zero, shift> { using Result = Zero; }; template<size_t shift> struct SmallShiftRight<Zero, shift> { using Result = Zero; static const uint32_t carry = 0; }; template<uint32_t... a> struct BigShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct BigShiftRight <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct SmallShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct SmallShiftRight<BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; static const uint32_t carry = 0; };

実装が大きく異なるため、ビットシフトを小さな（32ビット未満のシフト）と大きな（32ビットの倍数のシフト）の連続したアプリケーションに分割することは論理的であると判断しました。したがって、大きな変化：

 template<uint32_t... a, size_t shift> struct BigShiftLeft<BigUnsigned<a...>, shift> { using Result = typename Concatenate< BigUnsigned<0>, typename BigShiftLeft< BigUnsigned<a...>, shift - 1 >::Result >::Result; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct BigShiftRight<BigUnsigned<a_0, a_tail...>, shift> { using Result = typename BigShiftRight< BigUnsigned<a_tail...>, shift - 1 >::Result; };

ここで、シフトとは32⋅シフトビットのシフトを意味し、演算自体は単純に32ビットワード全体を交互に「消費」または追加します。

小さなシフトはすでにもう少し微妙な作業です。

 template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct SmallShiftLeft<BigUnsigned<a_0, a_tail...>, shift> { static_assert(shift < 32, "shift in SmallShiftLeft must be less than 32 bits"); static const uint32_t carry = a_0 >> (32 - shift); using Result = typename Concatenate< BigUnsigned<(a_0 << shift)>, typename Sum< //   Or  Xor,  Sum     typename SmallShiftLeft<BigUnsigned<a_tail...>, shift>::Result, BigUnsigned<carry> >::Result >::Result; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct SmallShiftRight<BigUnsigned<a_0, a_tail...>, shift> { static_assert(shift < 32, "shift in SmallShiftRight must be less than 32 bits"); static const uint32_t carry = a_0 << (32 - shift); using Result = typename Concatenate< BigUnsigned<(a_0 >> shift) | SmallShiftRight<BigUnsigned<a_tail...>, shift>::carry>, typename SmallShiftRight<BigUnsigned<a_tail...>, shift>::Result >::Result; };

ここでも、正確なビット転送に注意する必要があります。

最後に、ただのシフト：

 template<class A, size_t shift> struct ShiftLeft { using Result = typename BigShiftLeft< typename SmallShiftLeft<A, shift % 32>::Result, shift / 32 >::Result; }; template<class A, size_t shift> struct ShiftRight { using Result = typename SmallShiftRight< typename BigShiftRight<A, shift / 32>::Result, shift % 32 >::Result; };

約束どおり、彼は大小のシフトを賢く使用しています。

比較操作の実装

 template<class A, class B> struct GreaterThan; template<class A, class B> struct GreaterThanOrEqualTo; template<class A> struct GreaterThan<Zero, A> { static const bool value = false; }; template<class A> struct GreaterThanOrEqualTo<Zero, A> { static const bool value = false; }; template< > struct GreaterThanOrEqualTo<Zero, Zero> { static const bool value = true; }; template<uint32_t n, uint32_t... tail> struct GreaterThanOrEqualTo<BigUnsigned<n, tail...>, Zero> { static const bool value = true; }; template<uint32_t n, uint32_t... tail> struct GreaterThan<BigUnsigned<n, tail...>, Zero> { static const bool value = n > 0 || GreaterThan<BigUnsigned<tail...>, Zero>::value; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct GreaterThan<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { using A_tail = BigUnsigned<a_tail...>; using B_tail = BigUnsigned<b_tail...>; static const bool value = GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n > b_n); }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct GreaterThanOrEqualTo<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { using A_tail = BigUnsigned<a_tail...>; using B_tail = BigUnsigned<b_tail...>; static const bool value = GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n >= b_n); }; template<class A, class B> struct LessThan { static const bool value = !GreaterThanOrEqualTo<A, B>::value; }; template<class A, class B> struct LessThanOrEqualTo { static const bool value = !GreaterThan<A, B>::value; };

分割。予想どおりに始めましょう：クラスの定義と再帰ベースの定義から。

 template<class A, class B> struct Division; template<class A> struct Division<A, Zero> { using Quotient = DivisionByZeroError; using Residue = DivisionByZeroError; }; template<uint32_t n, uint32_t... tail> struct Division<BigUnsigned<n, tail...>, One> { using Quotient = BigUnsigned<n, tail...>; using Residue = Zero; }; template<class A, class B> struct DummyDivision { using Quotient = Zero; using Residue = A; };

ここで、追加のダミークラスstruct DivisionByZeroError {}

を導入しました。

その唯一の機能は、プログラマの平凡な生活をわずかに明るくすることです。

定型プログラムをデバッグしようとしています。したがって、次の形式のプログラムをコンパイルしようとすると

 int main(...) { ... std::cout << BinaryRepresentation<typename Division<One, Zero>::Quotient>::str() << std::endl; ... }

clangは次のような警告を表示します

 static_bignum.cpp:229:18: error: implicit instantiation of undefined template 'BinaryRepresentation<DivisionByZeroError>'

なぜ神秘的なDummyDivision

クラスが必要なのDummyDivision

、今から見てみましょう。

したがって、除算アルゴリズム自体は、最も単純な（そしておそらく非常に非効率的）ものを使用します。 AをBで除算します。AがBより小さい場合、解は明らかです。剰余はA、商は0です（実際、明白な除算は補助クラスDummyDivision

も生成します）。そうでない場合、QをAを2Bで除算した結果とします。 Rはこの除算の剰余、つまりA = 2BQ + R

次に、明らかに、 A / B = 2Q + R / B

; ただし、Rは2B未満であることが保証されているため、 R / B

は0または1のいずれかです。次に、 A % B = R % B

で、 R % B

はRまたはR - B

いずれかですR - B

実際には、コード：

 template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct Division<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { private: using A = BigUnsigned<a_n, a_tail...>; //      ..  .. using B = BigUnsigned<b_n, b_tail...>; using D = typename std::conditional< //  :   2B GreaterThanOrEqualTo<A, B>::value, Division<A, typename SmallShiftLeft<B, 1>::Result>, DummyDivision<A, B> // (  ) >::type; using Q = typename D::Quotient; //   using R = typename D::Residue; public: using Quotient = typename Sum< //  2Q (,  ,  Q << 1)  R / B typename SmallShiftLeft<Q, 1>::Result, typename std::conditional<GreaterThanOrEqualTo<R, B>::value, One, Zero>::type //  <type_traits>  std::conditional,  //    ,      >::Result; using Residue = typename std::conditional< GreaterThanOrEqualTo<R, B>::value, typename Difference<R, B>::Result, R >::type; };

IIIii最終的に10進表記！数値の10進表現を印刷するには、10で長時間除算できることは明らかです。最初の除算の残りは最小の符号を与え、最初の商の除算の残りの10は2番目の符号を与えるというようになります。ただし、C ++では、数字を数字ごとに印刷する必要はありません。たとえば、100で数値を除算して、一度に2つの符号を取得できます。したがって、 uint32_t

に収まる最大数、つまり10 ⁹でuint32_t

ます。

 template<class A> struct DecimalRepresentation; template<> struct DecimalRepresentation<Zero> { static inline std::string str(void) { return "0"; } }; template<class A> struct Digit; // ,       template<> struct Digit<Zero> { static const uint32_t value = 0; }; template<uint32_t digit, uint32_t... tail> struct Digit<BigUnsigned<digit, tail...>> { static const uint32_t value = digit; }; template<uint32_t n, uint32_t... tail> struct DecimalRepresentation<BigUnsigned<n, tail...>> { private: static const uint32_t modulo = 1000000000UL; static const uint32_t modulo_log = 9; using D = Division<BigUnsigned<n, tail...>, BigUnsigned<modulo>>; using Q = typename D::Quotient; using R = typename D::Residue; static_assert(Digit<R>::value < modulo, "invalid division by power of 10"); public: static std::string str(void) { //  C++     ,        . //      ,   . std::string stail = DecimalRepresentation<Q>::str(); //    if(stail == "0") stail = ""; std::string curr = std::to_string(Digit<R>::value); //     if(stail != "") while(curr.size() < modulo_log) curr = "0" + curr; return stail + curr; } };

そして最後に、私たちのコード

 using A = BigUnsigned<0xFFFFFFFFULL>; using B = One; using C = Sum<A, B>::Result; int main(int argc, char** argv) { std::cout << DecimalRepresentation<C>::str() << std::endl; }

4294967296

を4294967296

。これは正確に2 ³²です。

すべてのコードをまとめて

 #include <cstdint> #include <bitset> #include <iostream> #include <algorithm> #include <type_traits> template<uint32_t... digits> struct BigUnsigned { static const size_t length = sizeof...(digits); }; using Zero = BigUnsigned< >; using One = BigUnsigned<1>; template<class A, class B> struct Concatenate { using Result = void; }; template<uint32_t... a, uint32_t... b> struct Concatenate<BigUnsigned<a...>, BigUnsigned<b...>> { // >> -    C++11 using Result = BigUnsigned<a..., b...>; }; template<class A, class B> struct Sum; template<class A> struct Sum<Zero, A> { using Result = A; }; template<class A> struct Sum< A, Zero> { using Result = A; }; //       ,      : template< > struct Sum<Zero, Zero> { using Result = Zero; }; template<uint32_t a_0, uint32_t... a_tail, uint32_t b_0, uint32_t... b_tail> struct Sum<BigUnsigned<a_0, a_tail...>, BigUnsigned<b_0, b_tail...>> { static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0; using Result = typename Concatenate< BigUnsigned<a_0 + b_0>, typename Sum< typename Sum< BigUnsigned<a_tail...>, BigUnsigned<b_tail...> >::Result, BigUnsigned<carry> >::Result >::Result; }; template<class A> struct BinaryRepresentation; template<uint32_t a_0, uint32_t... a> struct BinaryRepresentation<BigUnsigned<a_0, a...>> { static std::string str(void) { std::bitset<32> bset(a_0); return BinaryRepresentation<BigUnsigned<a...>>::str() + bset.to_string(); } }; template<> struct BinaryRepresentation<Zero> { static std::string str(void) { return "0b"; // Oppa Python Style } }; template<class A, class B> struct Difference; struct OverflowError {}; template<> struct Difference<Zero, Zero> { using Result = Zero; }; template<uint32_t n, uint32_t... tail> struct Difference<BigUnsigned<n, tail...>, Zero> { using Result = BigUnsigned<n, tail...>; }; template<uint32_t n, uint32_t... tail> struct Difference<Zero, BigUnsigned<n, tail...>> { using Result = OverflowError; }; template<class A> struct Difference<OverflowError, A> { using Result = OverflowError; }; template<class A> struct Difference<A, OverflowError> { using Result = OverflowError; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct Difference<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...> > { using A = BigUnsigned<a_n, a_tail...>; //      using B = BigUnsigned<b_n, b_tail...>; using C = typename Difference<BigUnsigned<a_tail...>, BigUnsigned<b_tail...>>::Result; using Result_T = typename std::conditional< //    ? a_n >= b_n, C, typename Difference<C, One>::Result >::type; using Result = typename std::conditional< //     a_n == b_n && std::is_same<Result_T, Zero>::value, Zero, typename Concatenate< BigUnsigned<a_n - b_n>, Result_T >::Result >::type; }; template<class A, size_t shift> struct ShiftLeft; template<class A, size_t shift> struct ShiftRight; template<class A, size_t shift> struct BigShiftLeft; template<class A, size_t shift> struct BigShiftRight; template<class A, size_t shift> struct SmallShiftLeft; template<class A, size_t shift> struct SmallShiftRight; template<size_t shift> struct BigShiftLeft <Zero, shift> { using Result = Zero; }; template<size_t shift> struct BigShiftRight <Zero, shift> { using Result = Zero; }; template<size_t shift> struct SmallShiftLeft <Zero, shift> { using Result = Zero; }; template<size_t shift> struct SmallShiftRight<Zero, shift> { using Result = Zero; static const uint32_t carry = 0; }; template<uint32_t... a> struct BigShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct BigShiftRight <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct SmallShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct SmallShiftRight<BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; static const uint32_t carry = 0; }; template<uint32_t... a, size_t shift> struct BigShiftLeft<BigUnsigned<a...>, shift> { using Result = typename Concatenate< BigUnsigned<0>, typename BigShiftLeft< BigUnsigned<a...>, shift - 1 >::Result >::Result; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct BigShiftRight<BigUnsigned<a_0, a_tail...>, shift> { using Result = typename BigShiftRight< BigUnsigned<a_tail...>, shift - 1 >::Result; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct SmallShiftLeft<BigUnsigned<a_0, a_tail...>, shift> { static_assert(shift < 32, "shift in SmallShiftLeft must be less than 32 bits"); static const uint32_t carry = a_0 >> (32 - shift); using Tail = typename Sum< //    Or  Xor,  Sum     typename SmallShiftLeft<BigUnsigned<a_tail...>, shift>::Result, BigUnsigned<carry> >::Result; using Result = typename std::conditional< std::is_same<Tail, BigUnsigned<0>>::value, //   ,   (!) BigUnsigned<(a_0 << shift)>, typename Concatenate< BigUnsigned<(a_0 << shift)>, Tail >::Result >::type; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct SmallShiftRight<BigUnsigned<a_0, a_tail...>, shift> { static_assert(shift < 32, "shift in SmallShiftRight must be less than 32 bits"); static const uint32_t carry = a_0 << (32 - shift); using Result = typename Concatenate< BigUnsigned<(a_0 >> shift) | SmallShiftRight<BigUnsigned<a_tail...>, shift>::carry>, typename SmallShiftRight<BigUnsigned<a_tail...>, shift>::Result >::Result; }; template<class A, size_t shift> struct ShiftLeft { using Result = typename BigShiftLeft< typename SmallShiftLeft<A, shift % 32>::Result, shift / 32 >::Result; }; template<class A, size_t shift> struct ShiftRight { using Result = typename SmallShiftRight< typename BigShiftRight<A, shift / 32>::Result, shift % 32 >::Result; }; template<class A, class B> struct GreaterThan; template<class A, class B> struct GreaterThanOrEqualTo; template<class A> struct GreaterThan<Zero, A> { static const bool value = false; }; template<class A> struct GreaterThanOrEqualTo<Zero, A> { static const bool value = false; }; template< > struct GreaterThanOrEqualTo<Zero, Zero> { static const bool value = true; }; template<uint32_t n, uint32_t... tail> struct GreaterThanOrEqualTo<BigUnsigned<n, tail...>, Zero> { static const bool value = true; }; template<uint32_t n, uint32_t... tail> struct GreaterThan<BigUnsigned<n, tail...>, Zero> { static const bool value = n > 0 || GreaterThan<BigUnsigned<tail...>, Zero>::value; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct GreaterThan<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { using A_tail = BigUnsigned<a_tail...>; using B_tail = BigUnsigned<b_tail...>; static const bool value = GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n > b_n); }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct GreaterThanOrEqualTo<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { using A_tail = BigUnsigned<a_tail...>; using B_tail = BigUnsigned<b_tail...>; static const bool value = GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n >= b_n); }; template<class A, class B> struct LessThan { static const bool value = !GreaterThanOrEqualTo<A, B>::value; }; template<class A, class B> struct LessThanOrEqualTo { static const bool value = !GreaterThan<A, B>::value; }; struct DivisionByZeroError { }; template<class A, class B> struct Division; template<class A> struct Division<A, Zero> { using Quotient = DivisionByZeroError; using Residue = DivisionByZeroError; }; template<uint32_t n, uint32_t... tail> struct Division<BigUnsigned<n, tail...>, One> { using Quotient = BigUnsigned<n, tail...>; using Residue = Zero; }; template<class A, class B> struct DummyDivision { using Quotient = Zero; using Residue = A; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct Division<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { private: using A = BigUnsigned<a_n, a_tail...>; using B = BigUnsigned<b_n, b_tail...>; using D = typename std::conditional< GreaterThanOrEqualTo<A, B>::value, Division<A, typename SmallShiftLeft<B, 1>::Result>, DummyDivision<A, B> >::type; using Q = typename D::Quotient; using R = typename D::Residue; public: using Quotient = typename Sum< typename SmallShiftLeft<Q, 1>::Result, typename std::conditional<GreaterThanOrEqualTo<R, B>::value, One, Zero>::type >::Result; using Residue = typename std::conditional< GreaterThanOrEqualTo<R, B>::value, typename Difference<R, B>::Result, R >::type; }; template<class A> struct DecimalRepresentation; template<> struct DecimalRepresentation<Zero> { static inline std::string str(void) { return "0"; } }; template<class A> struct Digit; template<> struct Digit<Zero> { static const uint32_t value = 0; }; template<uint32_t digit, uint32_t... tail> struct Digit<BigUnsigned<digit, tail...>> { static const uint32_t value = digit; }; template<uint32_t n, uint32_t... tail> struct DecimalRepresentation<BigUnsigned<n, tail...>> { private: static const uint32_t modulo = 1000000000UL; static const uint32_t modulo_log = 9; using D = Division<BigUnsigned<n, tail...>, BigUnsigned<modulo>>; using Q = typename D::Quotient; using R = typename D::Residue; static_assert(Digit<R>::value < modulo, "invalid division by power of 10"); public: static std::string str(void ){ std::string stail = DecimalRepresentation<Q>::str(); if(stail == "0") stail = ""; std::string curr = std::to_string(Digit<R>::value); if(stail != "") while(curr.size() < modulo_log) curr = "0" + curr; return stail + curr; } }; using A = BigUnsigned<0xFFFFFFFFULL>; using B = One; using C = Sum<A, B>::Result; int main(int argc, char** argv) { std::cout << DecimalRepresentation<C>::str() << std::endl; }

他に言わなければならないこと

第一に、これが我々の長い算術の準備ができている場所であるとは言えません。

ここに多くを追加できます：乗算（列内）、べき乗、

ユークリッドアルゴリズムですら。BigSigned<int, uint32_t...>

記号付きの長い数字のクラスとそのすべての基本操作を定義する方法は簡単に理解できます。

第二に、バグ。すべてのコードはトレーニング用であり、おそらくデバッグが必要です。

（テンプレートの前に表示されるバージョンは、可変引数を使用してデバッグしましたが、残念ながら、

1つのコンパイラーのみでした。）少なくともトレーニング目標が達成されたことを期待しましょう。

第三に、長い演算は理想的な例からはほど遠いことを認めなければなりません。

可変引数テンプレートの威力を示すため。この機能を使用した興味深い実用的な例をご覧になった場合は、コメント内のリンクを共有してください。

C ++ 11の可変長テンプレートとコンパイル時の長い演算

パラメータパック

長い演算

他に言わなければならないこと

More articles: