- ランタイム-保証O(nlogn)。
- O(1)追加メモリを使用します。
- 単一リンクリストのデータの並べ替えの適用可能性(ただし、これに限定されません)。
3つの制限すべての予約:
- 保証されたO(nlogn)は、たとえば、クイックソートの平均時間が適切でないことを意味します。O(nlogn)は、最悪の入力であっても取得する必要があります。
- 再帰は、再帰呼び出しのスタックを格納するためのO(logn)メモリを意味するため、使用できません。
- ソートされた配列の要素への任意のアクセスはありません。イテレータを任意の要素から隣接する要素(O(1)を超える)にのみ移動し、一方向(リストの前方)にのみ移動できます。 リスト自体を変更することはできません(次の要素へのポインタを上回るため)。
配列の要素について知っているすべての情報は、それらがすべて線形に順序付けられたセットを形成するということです。 できることは、配列の2つの要素を比較し(O(1)の場合)、それらを交換することです(O(1)の場合も)。
カットの下で、私たちに何が起こったのかを知ることができます。
挑戦する 猫の下を見る前に、まずアルゴリズムについて自分で考えることをお勧めします。 あなたが私たちのオプションよりもクールな何かを思いついたら-コメントを書いてください。
ご予約
記事を徹底的に検索しなかったことを予約します-すでに既知のアルゴリズムを再度開いたか、この問題を解決するアルゴリズムが長い間知られています(おそらく私たちよりもはるかに効果的です)。
私たちのアルゴリズムの実用的な応用はほとんど不可能であり、タスクは学術的な関心のより多くのものです。
情報収集
すぐに頭に浮かぶ既知の種類は、3つのポイントすべてを同時に満たすわけではありません。次に例を示します。
- バブルソート(バブルソート)は、パラグラフ2および3に適合しますが、O(n 2 )に対して機能します。
- クイックソートはポイント2と3を満たします(ポイント2-いくつかのアイデアの知識があります)が、ポイント1については平均でO(nlogn)時間のみを与え、Oに対して機能する入力データがあります(n 2 )。
- ヒープの並べ替えは制限1と2を満たしますが、残念ながらメモリへのランダムアクセスが必要です。
- マージソートは制限1および3に適していますが、O(n)追加メモリが必要です。
- インプレースマージソートは制限1および2に適合します( 安定したオプションもありますが 、錫です)が、メモリにランダムアクセスせずに効果的に実装する方法は完全に不明です。
中央値またはBFPRTアルゴリズムの中央値
最初のコメントでは、FordPerfectの友人がMedian of Mediansアルゴリズムを提案しましたが、これは広く知られていませんでした。 彼の別の名前は、それを発明した科学者の名前に由来するBFPRTです。マヌエルBラム、ロバートW.フロイド、ウォンプラット、ロナルドL.リベスト、ロバートE. Tアリアン。 アルゴリズムはWikipedia( ru 、 en )、およびKormenで説明されていますが、Wikipediaではロシア語と英語版を比較して初めてその本質を理解できるほど不器用であるため、少し説明します( 元の記事も調べなければなりませんでした) ) そして、Habréでの彼の説明はまだありませんでした。 コーメンでは、どちらかといえば説明は正常ですが、後でこのアルゴリズムが存在することがわかりました。 このアルゴリズムを既に知っている場合は、この記事の一部をスキップできます。
Median of Mediansアルゴリズムにより、最悪の場合、線形時間で任意の配列のk番目の順序統計を見つけることができます。 C ++ STLライブラリには、同様のアルゴリズムstd :: nth_elementがあります。これは、Quickselectアルゴリズムに基づいているため、線形時間のk番目の順序統計も検出します。 後者は基本的にクイックソートで、各ステップで再帰の分岐を1つだけ下っていきます(Quickselectの詳細については、 こちらとこちらをご覧ください )。 Median of Mediansは、Quickselectアルゴリズムの修正であり、「分岐」の悪い要素を選択することはできません。最悪の場合、二乗時間になります。
なぜ中央値の中央値が必要なのですか? はい、すべてが非常に単純です-その助けを借りて、線形時間で配列の中央値(n / 2次統計)を見つけ、この要素で高速ソートアルゴリズムを分岐することが可能です。 これにより、O(nlogn)に対して平均ではなく、最悪の場合にクイックソートが機能します。
Medians of Mediansアルゴリズムの説明。 入力データ:配列(たとえば、リストの最初と最後の要素で指定される)と数値k-どのアカウント要素を見つける必要があるか。
- 配列が十分に小さい場合(5要素未満)-おでこで泡でソートし、k番目の要素を返します。
- 配列のすべての要素を5つの要素のブロックに分割します。 不完全な最終ブロックの可能性に注意を払っていません。
- 各ブロックでは、要素をバブルで並べ替えます。
- 各ブロックの中央(3番目)の要素からサブアレイを選択します。 単純に配列の先頭に移動できます。
- これらの[n / 5]要素の中央値の中央値を再帰的に起動し、それらの中央値(n / 10番目の要素)を見つけます。 この要素はピボット要素と呼ばれます。
- おそらく、クイックソートとクイックセレクトアルゴリズムでよく知られている分離手順を実行しています。参照要素よりも小さい要素をすべて配列の先頭に移動し、すべての要素を末尾に移動します。 配列の最後にある可能性のある不完全なブロックの要素も考慮されます。 合計で、3つのブロックが得られます。要素は、基本よりも小さく、それと同等であり、それ以上です。
- どのブロックでk番目の要素を探す必要があるかを決定します。 2番目のブロックにある場合、そこから任意の要素を返します(すべて同じです)。 そうでない場合、要素番号を修正できるこのブロックの中央値の中央値を再帰的に起動します。3番目のブロックでは、番号kから前のブロックの長さを減算する必要があります。
ここで何が起こっているかの例を見てみましょう。 配列があり、その中央値を見つけたいとしましょう:

1から27までの27の異なる番号があります。連続して14番目の要素を探しています。 要素を長さ5のブロックに分割し、各ブロック内の数字を並べ替えます。

各ブロックの中央値は黄色で強調表示されます。 それらを配列の先頭に移動し、アルゴリズムを再帰的に実行して、その中の中央値を検索します。

再帰の内部で何が起こるかを書き留めません。1つはっきりしていることは、12が望ましい中央値になることです。

この数値12-中央値の支持要素または中央値-は、次の顕著な特性を持っています。 数枚の写真に戻って、次のようにブロックを精神的に動かしてみましょう。
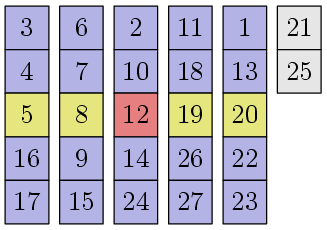
すべての列は中央の要素でソートされ、さらに各列の要素もソートされます。 支持要素の左上にある要素の約30%(正確には3 / 10n + O(1))は、それより大きくないことがわかります。 同様に、サポート要素の右下にある要素の約30%については、それ以上です。 つまり、分離手順を実行すると、すべての要素の約30%が必然的に支持要素の左側に、約30%が右側になります。

実際、わずかな不正確さがあります。幸運なことに、参照要素に等しい要素が1つだけ存在するという事実がありました。 そのような要素が多数ある場合、それらはすべてブロック全体を形成し、サポート要素が正確にどこに収まるかは明確ではありません。 しかし、それは本当に重要ではありません。 支持要素以上の要素は少なくとも30%であることがわかっています。つまり、支持要素より厳密に小さい要素は70%以下です。 同様に、サポート要素よりも厳密に大きい要素も70%以下です。 したがって、上記のアルゴリズムの説明からの最初と3番目のブロックのサイズは、常に7 / 10n + O(1)以下の長さを持ちます!

例の分析を続けます。 分離手順の後、14番目の要素が3番目のブロックにあることが明らかになるため、そのアルゴリズム全体を再帰的に実行しますが、現在は2番目の要素を探しています。
アルゴリズムの複雑さは何ですか?
T(n)を、長さnの配列に対するMedian of Mediansアルゴリズムの最悪の場合の数演算とします。 各ステップで、アルゴリズムは自身を2回再帰的に2回呼び出します。 最初は、長さがn / 5 + O(1)個の要素の配列で中央値の中央値を見つけることです。 2回目-探索空間を縮小しますが、最悪の場合、配列のサイズは7 / 10n + O(1)に減少します。 他のすべての操作には線形時間が必要です。 合計は比率を取得します:
T(n)= T(2 / 10n)+ T(7 / 10n)+ Cn、ここでCは定数です。
この関係を拡張しましょう。
T(n)= Cn +( 2/10 + 7/10 )Cn +( 2/10 + 7/10) ( 2/10 + 7/10 )Cn + ... = Cn * ∑ i =0..∞ ( 9/10) i = 10Cn = O(n)
いいね! アルゴリズムには線形の複雑さがあります!
Median of Mediansは、再帰を使用してリストに簡単に実装できます。これにより、O(logn)メモリを使用した単一リンクリストでのO(nlogn)の並べ替えが保証されます。
コード
ここで再帰を取り除きましょう。
フラットクイックソート
始めるために、実際にはクイックソートから再帰を削除しましょう。 これを行う方法は完全に明らかではないため、このセクションではその方法を説明します。
このセクションでは、Comdade FordPerfectがgamedev.ruフォーラムで提案したアイデアについて説明します(実際、この記事のすべてのアイデアは私のものではありません-ちょうど投稿しました)。 アイデアの出所は不明で、Googleはほとんどの部分で沈黙し、スタックがかなり頻繁にエミュレートされるいわゆる反復クイックソートへの多くのリンクを提供します(ただし、同様のアイデアの議論がありました)。 「O(1)メモリを備えたクイックソート」タスクについて考える時間。 「Flat quick sort」という名前も自作です。おそらく、このアルゴリズムは別の名前で知られています。
通常の再帰クイックソートがどのように機能するかを思い出しましょう。 入力データ:たとえば、単純に接続されたリストの開始要素と終了要素の2つの反復子によって指定される配列。
- 1つのパスをチェックインします。配列が既にソートされている場合、実行することはありません-終了します。
- 分離手順の要素(ピボット)を選択します-通常はランダムですが、この場合は、Median of Mediansアルゴリズムを使用して中央値を選択します。
- 分離手順を作成します-3つのブロックを取得します。ピボットよりも小さい要素。 彼に等しい要素; 要素が大きくなります。
- 最初と3番目のブロックに対して再帰的にクイックソートを実行します。
再帰中に覚えておく必要がある情報は、3番目のブロックの始まりと終わりです。
次のことに注意してください。最初のブロックの要素は2番目のブロックの要素よりも小さく、2番目のブロックの要素は3番目のブロックの要素よりも小さくなります。
考え方は次のとおりです。各ブロックの最大要素をブロックの先頭に移動しましょう。 その後、次のブロックがどこから始まるかを明確に決定できます! これを行うには、ブロックの先頭から厳密に大きい要素に出会うまで移動します。次のブロックの先頭を通知します!
これで、クイックソートアルゴリズムを次のように書き換えることができます。
- ポインターXとYを作成します。ポインターXが配列の先頭を指し、ポインターYがその末尾を指すようにします。 また、現在のブロックの終わりを指すポインターZを作成します。 最初は、Z = Yです。
- 次のアクションを際限なく実行します。
- 現在のXZブロックが既にソートされている場合、次のブロックを探します。 XをZに続く要素に移動します。Xを移動できない場合、Z = Yであるため、ループを終了します。 ここで、Xが指す要素よりも大きい、Xの後の最も近い要素aを探します。ない場合は、Z = Yを実行します。
- クイックソートの通常のアクションを実行します。分離する要素の選択と分離自体です。 3つのブロックを取得します。
- 3番目のブロックのブロック化を行います。その中の最大要素を探して、先頭に移動します。
- Zを最初のブロックの最後に移動します。
次に、例を使用してこのアルゴリズムを検討します。

私はすでにこの配列を見ました...ポインターX、Y、Zを入れましょう:

XZブロックはソートされません。 次に、中央値を見つけます。

中央値検索手順は、最も奇妙な方法で要素をシャッフルし、中央値自体を最初に残すと仮定します(例として、実装は、中央値である要素に反復子を返す場合があります)。 では、分離手順を実行しましょう。

それは3ブロックになりました。 最後のブロックをブロックし、Zを最初のブロックの最後に移動します。

今、私たちは最初から始めます。 現在のXZブロックはソートされていないため、その中の中央値を探しています。

分離手順を実行します。

3番目のブロックをブロックし、Zを最初のブロックの最後に移動します。

もう一度、XZを見てください。

ラッキーです! ブロックはソートされているため、そのままにして次のブロックを探すことができます。 ポインターXとZは次のように移動します。

これは前のステップの2番目のブロックであるため、突然、このブロックもソートされます。 次のブロックを探しています:
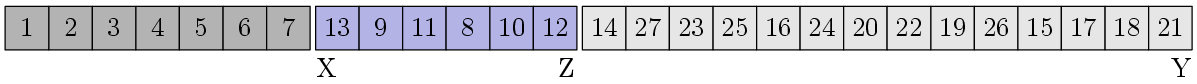
注文を確認します-残念ながら、今回は幸運ではなかったので、手配する必要があります。 中央値を見つけてから、分離手順を実行します。

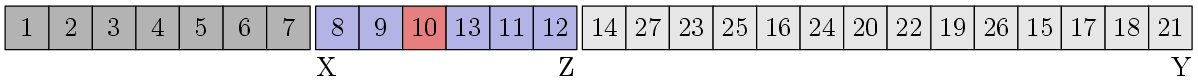
次に、ブロック[8,9]に移動し、ソートされます。そのため、XとZはブロック[10]に移動し、これもソートされます。その後、アルゴリズムはブロック[13、11、12]を考慮します。 。 アレイの後半のソート分析は、読者が個別に実行することを提案します。
コード
O(1)の追加メモリを備えた中央値のおおよその中央値
残念ながら、Median of Mediansでは、最大要素を使用してフラットクイックソートでブロックを識別するなどのトリックは機能しません。これは、毎回配列の要素が不明確に混在しているためです。 ここでは、別のフォーカスを使用します。
実際、保証されたO(nlogn)に対して迅速なソートを実行するために、分離段階の正確な中央値を見つける必要はありません。 近似値を見つけるだけで十分です。 特定のC <1について、分離段階後の最初と3番目のブロックがCnを超えないことを保証する場合、O(nlogn)のクイックソートが機能します。 C = 0.99でも。
したがって、メディアンの中央値を変更して、エラーK = O(log 2 n)の中央値を見つけます。 つまり、シリアル番号がn / 2-K / 2〜n / 2 + K / 2の範囲にある要素が見つかります。 Kは対数の次数であるため、セグメント[n / 2-K / 2、n / 2 + K / 2]が存在する(具体的には)nを見つけるのは簡単です。たとえば、1 / 4nと3 / 4nの間です。 すべての小さいnについて、バブルだけでソートできます。
なぜK = O(log 2 n)ですか? はい、K配列要素を使用して、スタックに必要なすべての情報を格納します(これもFordPerfectの仲間です)。 再帰レベルはO(logn)であり、それぞれについて、O(logn)ビットごとにO(1)の数値を格納する必要があります。 そして、残りのNK要素の中でクイックソートの中央値を見つけます。
各ビットは、配列の2つの連続する異なる要素によって表されます。 それらの最初の値が2番目の値より小さい場合、ビットは状態0を格納し、そうでない場合は-1(またはその逆)を格納します。 解決する必要がある最初のタスクは、配列の異なる要素のK / 2ペアを見つけ、あまり多くのペアが見つからない場合の対処方法を理解することです。
これは非常に簡単です。 反復子XとYが配列の最初の要素を指すようにします。 Xと等しくない要素が見つかるまでYを前方に移動します。それが見つかったら、Xを前方に移動し、XとYが指す要素を交換し、Xを前方に再度移動します(+小さい場合を引き続き処理する必要がある場合-Yを前方に移動しますXに直面した。 そして、K / 2ペアが見つかるまで。 Yがすでに配列の終わりに達し、K / 2ペアがまだ見つからない場合はどうなりますか? これは、XからYまでのすべての要素が同じであることを意味します! (この不変式がアルゴリズム全体の実行中に保存されることを確認するのは非常に簡単です)。 次に、サポート要素として、これらの要素の1つをすぐに選択できます。 K <n / 2を選択した場合、このサポート要素は正確な中央値になります。
さて、質問は次のとおりです。スタックを操作すると、アルゴリズムの漸近的な動作が壊れますか? これは非常に良い質問です。一見すると、再帰ツリーの頂点の順序はO(n)であり、各頂点に対してスタックでO(log 2 n)操作が必要だと思われるためです。 Median of Mediansの漸近的挙動はO(nlog 2 n)(およびアルゴリズム全体のO(nlog 3 n))に悪化していますか? ここではすべてが少し複雑です。
ツリー内の頂点の正確な数を計算するには、次の繰り返しを解決する必要があります。
N(n)= N(n / 5)+ N(7N / 10)+ 1
n <Cの場合、N(n)= 1
上記と似たようなものが見られますが、Cnを1に置き換えると、再帰の計算がやや難しくなります。 Acra-Bazzi方式が助けになります。 再帰はすべての条件に適合し、対応するすべての順列の後、頂点の数N(n)がO(n 0.84 )(より正確にはΘ(n 0.839780 ... ))として増加することがわかります 。 アルゴリズムの総時間複雑度はO(n + n 0.84 log 2 n)= O(n)です。
アルゴリズムのこれ以上のスペルは不要であると考えています。この記事の前の章のいずれかで説明されたものを実装するだけです。 コードをすぐに確認することをお勧めします。 画像もありません。アルゴリズムがまったく機能しないためには、配列内にかなり多くの要素が必要です。 どっち? 詳細については、以下をご覧ください。
提案されたアルゴリズムはどの程度非実用的ですか? 計算は次のとおりです。
実際の中央値から1 / 4n以下の偏差を取得するとします(つまり、K <n / 2)。 次に、3 [logn]再帰レベルでスタックをハンマーで打つ必要があります(ここで、logは2進数で、(3/4) 3 <0.5であり、[x]は数値xを最も近い整数に切り上げます)。 再帰レベルごとに2 [logn]ビットが必要です。現在の配列の長さ、現在探している要素(この数は常に[logn] -1ビットに収まります)およびトラバーサルツリーのトラバーサル順序を維持するためのもう1ビットを格納する必要があります(必要です)どの再帰分岐から戻ったかを思い出してください)。 各ビットには2つの要素があり、スタックごとに合計12 [logn] 2つの要素があります。
ここで方程式を解きます:12 [logn] 2 <n / 2または24 [logn] 2 <n。 nを見つける必要があります(n> = nの場合)24 [logn] 2 <n。 このn 'は3500のオーダーです。つまり、n <3500の場合、バブルでソートする必要があります。
Kが常にn-1500を超えないnの制限、つまり、n <1500の場合、ソートは機能しません(スタックをエミュレートするのに十分な要素がありません)。ここではためらうことなくバブルを使用する必要があります。 ただし、定数をいじると、おそらくこの推定値は改善される可能性があります。
コード
コード
記事全体のコードへのすべてのリンクを1か所で:
- クイックソート+中央値の中央値 (保証O(nlogn)、O(logn)の追加メモリ)
- フラットクイックソート+中央値の中央値 (保証O(nlogn)、O(logn)の追加メモリ)
- フラットクイックソート+中央値のおおよその中央値 (保証O(nlogn)、O(1)追加メモリ)
読む
- gamedev.ru のアルゴリズムの説明。
- ウィキペディアのメディアンの中央値( en 、 ru )。
- Quickselectについては、 こちらとこちらをご覧ください 。
- ウィキペディアのAcra-Bazziメソッド 。
- Manual Blum、Robert W. Floyd、Vaughan Pratt、Ronald L. Rivest、およびRobert E. Tarjan。 選択の時間範囲 。 (pdf、eng)
- S.バッティアト、D。カントン、D。カタラノ、G。シンコッティ。 近似中央値選択問題の効率的アルゴリズム 。 (pdf、eng)-高速の近似確率的中央値中央値