はじめに

この記事は、以前の出版物で始まったトピックの論理的な続きです。コメントで約束されているように、過剰な座標法の、乾燥クーロン摩擦力の影響下で動く機械システムの動的解析への適用可能性を検討します。実例として、次の問題を解決します

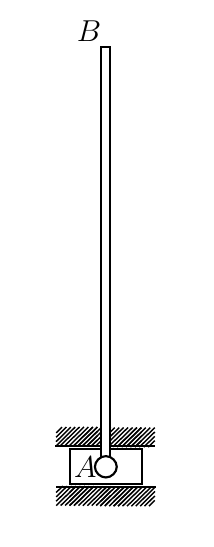
質量m = 2 kg、ポイントAの長さAB = 2 l = 1 mの細い均一なロッドは、水平ラフガイド内を移動する無重量スライダーに旋回可能に取り付けられています。最初は、ロッドは垂直に配置されており、その後、無視できる角度で垂直から偏向され、初期速度なしで解放されます。所定の機械システムの運動方程式を作成し、その運動の法則を見つける必要があります。スライダーとガイド間の摩擦係数はf = 0.1です。

著者が提案した方法による問題の解決に進む前に、乾式摩擦に関する少し初歩的な理論を考えてみましょう。

1.「簡単な」摩擦とは何ですか？

メカニックにとって、摩擦ほど悪い罰はありません。問題に現れると、この力はすぐに実質的に非線形になります。これは興味深い方法で動作するためです。

かなり単純な例を考えてみましょう。粗い表面に水平バーを置きます。

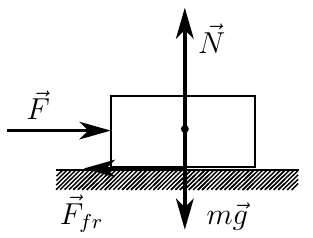
最初は力が加えられていないと仮定します（重力と通常の反応を除く）。この場合、バーと平面間の摩擦力はゼロになります。

次に、バーに小さな水平方向の力を加えます。表面からの衝撃に応答して、摩擦力がバーに作用し、条件を満たしますので、バーは動きません

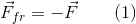
$\ vec {F} _ {fr} =-\ vec {F} \ quad \ quad（1）$

徐々に強度を上げていきます $\ vec {F}$ また、（1）によると、摩擦力も増加します。この場合、これは静的摩擦力と呼ばれます。これは、静止摩擦力が値に達するまで続きます

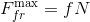
$F_ {fr} ^ {\ max} = fN$

静止摩擦力の限界値と呼ばれます。ここで、 fはバーと平面間の乾燥摩擦係数です。 N-飛行機からの通常の反応。この後、摩擦力は増加しなくなり、水平方向の力がさらに増加すると、バーのスライドが開始されます。摩擦力は、次と等しい摺動摩擦力に移行します。

$\ vec {F} _ {fr} = -fN \ cfrac {\ vec {v}} {\ left | \ vec {v} \ right |} \ quad \ quad（2）$

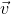どこで $\ vec {v}$ -バーの速度。

例は非常に簡単ですが、乾燥摩擦力の振る舞いの本質を明らかにしています。したがって、摩擦力を計算するための次のアルゴリズムを取得します。

摩擦力が適用される点が静止している場合：

静止摩擦力と垂直反力を計算します
状態を確認する

$F_ {fr} \ le fN$

これに違反して、最終的な静止摩擦力に等しい摩擦力を取ります

摩擦力の作用点が動く場合：

通常の反応を計算します
式（2）に従って、滑り摩擦力を計算します。

2.摩擦があるシステムの動きのモデリング

ここで問題を解決します。検討中のシステムには2つの自由度がありますが、通常の反応を決定する必要があるため、自由度の数を3に拡張し、次の計算スキームを取得します

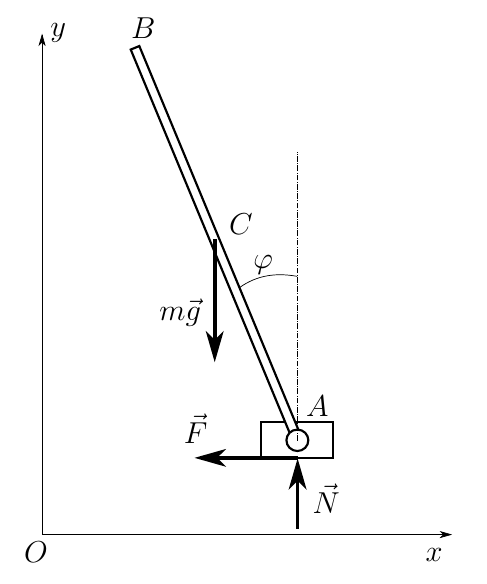
ここでは、ベクトルを一般化座標として取ります

$\ vec {q} = \左[x（t）、y（t）、\ varphi（t）\右] ^ T \ quad \ quad（3）$

ここで、 x、yはポイントAの座標です。 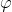$\バルフィ$ -垂直に対するロッドの傾斜角。メープルで武装

#   restart; #    with(LinearAlgebra): #    read `/home/maisvendoo/work/maplelibs/mechanics/lagrange.m`:

システムの運動学を決定する

 #    q := [x(t), y(t), phi(t)]: #   A xA := q[1]: yA := q[2]: #     xC := q[1] - L*sin(q[3]): yC := q[2] + L*cos(q[3]): # -  A  C rA := Vector([xA, yA]): rC := Vector([xC, yC]): #      VectorCalculus[BasisFormat](false): vC := VectorCalculus[diff](rC, t):

その運動エネルギーを計算する

 #       J := m*(2*L)^2/12: #    T := simplify(J*diff(q[3], t)^2/2 + m*DotProduct(vC, vC, conjugate=false)/2);

Mapleはこの結果を生成します

$T = 1/6 \、m \左（4 \、{L} ^ {2} \左（{\ frac {d} {dt}} \ phi \左（t \右）\右）^ {2} -6 \、L \左（{\ frac {d} {dt}} \ phi \左（t \右）\右）\左（{\ frac {d} {dt}} x \左（t \右）\右）\ cos \左（\ phi \左（t \右）\右）-6 \、L \左（{\ frac {d} {dt}} \ phi \左（t \右）\右）\左（{\ frac {d} {dt}} y \左（t \右）\右）\ sin \左（\ phi \左（t \右）\右）+3 \、\左（{ \ frac {d} {dt}} x \左（t \右）\右）^ {2} +3 \、\左（{\ frac {d} {dt}} y \左（t \右）\右）^ {2} \右）$

かなり面倒ですが、私たちを「摘む」ことは紙に手をかけることではないので、先に進みます。ベクトルと力の作用点を設定します

 #  ,    Mg := Vector([0, -m*g]): #   F_A := Vector([-F, 0]): #   N_A := Vector([0, N]): #   #    Fk := [Mg, F_A, N_A]: #      rk := [rC, rA, rA]:

システムの運動方程式を第2種ラグランジュの形で取得します。

 #    2  EQs := LagrangeEQs(T, q, rk, Fk):

3つの「ワニ」が手に入ります

$\ frac {4} {3} mL ^ 2 \ ddot {\ varphi} -mL \ ddot {y} \ sin \ varphi-mL \ ddot {x} \ cos \ varphi = mgL \ sin \ varphi \ quad \ quad（ 4）$

$m \ ddot {y} -mL \ dot {\ varphi} ^ 2 \ cos \ varphi-mL \ ddot {\ varphi} \ sin \ varphi = N-mg \ quad \ quad（5）$

$m \ ddot {x} + mL \ dot {\ varphi} ^ 2 \ sin \ varphi-mL \ ddot {\ varphi} \ cos \ varphi = -F \ quad \ quad（6）$

MapleのLaTeX出力の「コピー＆ペースト」により、結果が見苦しくなってしまうため、これらの方程式を手動で記事に組み込む必要がありました。しかし、たとえそうであっても、方程式は複雑であり、 Fが摩擦力であるという事実を考えると、分析的に積分可能ではありません。

次に、制約の方程式を紹介します。まず、スライダーは水平ガイドに沿って移動するため、

$y（t）= 0 \ quad \ quad（7）$

また、スライダーが静止していて、静止摩擦力が制限値を超えない場合、もう1つの接続がオンになります

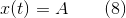
$x（t）= A \ quad \ quad（8）$

どこで $A = \ text {const}$ -スライダーの水平座標。次に、方程式（7）および（8）を考慮してシステム（4）-（6）を変換し、静止摩擦力と垂直反力を求めます。

 #   link_eq1 := q[1] = A: #  ,    -    link_eq2 := q[2] = 0: #     X Link_EQs := {link_eq1, link_eq2}: #           Reduced_EQs := ReduceSystem(EQs, Link_EQs, q): solv_reduced := SolveAccelsReacts(Reduced_EQs, [q[3]], [F, N]): #     for i from 1 to numelems(solv_reduced) do if has(solv_reduced[i], F) then F1 := rhs(solv_reduced[i]); end if; if has(solv_reduced[i], N) then N1 := rhs(solv_reduced[i]); end if; end do:

ここでは、Mapleが直接発行した結果を示します

$F_1 = -mL \ sin \ left（\ phi \ left（t \ right）\ right）\ left（{\ frac {d} {dt}} \ phi \ left（t \ right）\ right）^ {2} +3/4 \、\ cos \ left（\ phi \ left（t \ right）\ right）mg \ sin \ left（\ phi \ left（t \ right）\ right）\ quad \ quad（9）$

$N_1 = -mL \ cos \ left（\ phi \ left（t \ right）\ right）\ left（{\ frac {d} {dt}} \ phi \ left（t \ right）\ right）^ {2} -3/4 \、\左（\ sin \左（\ phi \左（t \右）\右）\右）^ {2} mg + mg \ quad \ quad（10）$

結果の式を見ると、それらはプロセスのロジックと一致しています。スライダーがガイドに沿ってスライドする場合の通常の反応を計算する式を取得します。この場合、摩擦力は式によって決定されます

$F = fN \ text {sign} \ left（\ dot {x} \ right）$

（マイナスはすでに運動方程式に含まれています）

 #          Slade_EQs := ReduceSystem(EQs, {link_eq2}, q): #        for i from 1 to numelems(Slade_EQs) do Slade_EQs[i] := subs(F = f*N*signum(diff(q[1], t)), Slade_EQs[i]); end do: solv_slade := SolveAccelsReacts(Slade_EQs, [q[1], q[3]], [N]): #      for i from 1 to numelems(solv_reduced) do if has(solv_slade[i], N) then N2 := rhs(solv_slade[i]); end if; end do:

うーん、特にMapleがLaTeXコードをかなり冗長に生成することを考えると、「ワニ」もリリースされました

$N_2 =-{\ frac {m \ left（3 \、L \ left（{\ frac {d} {dt}} \ phi \ left（t \ right）\ right）^ {2} \ left（\ cos \左（\ phi \左（t \右）\右）\右）^ {3} +3 \、L \左（{\ frac {d} {dt}} \ phi \左（t \右）\右）^ {2} \ cos \ left（\ phi \ left（t \ right）\ right）\ left（\ sin \ left（\ phi \ left（t \ right）\ right）\ right）^ {2}- 4 \、L \ cos \左（\ phi \左（t \右）\右）\左（{\ frac {d} {dt}} \ phi \左（t \右）\右）^ {2} -3 \、\ left（\ cos \ left（\ phi \ left（t \ right）\ right）\ right）^ {2} g-3 \、\ left（\ sin \ left（\ phi \ left（t \右）\右）\右）^ {2} g + 4 \、g \右）} {3 \、f \ sin \左（\ phi \左（t \右）\右）\ cos \左（ \ phi \ left（t \ right）\ right）{\ it \ text {sign}} \ left（{\ frac {d} {dt}} x \ left（t \ right）\ right）+3 \、\左（\ cos \左（\ phi \左（t \右）\右）\右）^ {2} -4}} \ quad \ quad（11）$

必要なすべての表現を受け取ったので、モデリングに進むことができます。すでに書いた振り子の問題とは対照的に、ここでは、数値解に適した形式にMapleツールを使用して方程式を正直に変換します。まず、一般化された加速度に関する方程式（4）-（6）を解きます

 #        Main_EQs := SolveAccelsReacts(EQs, q, []): #    s := numelems(q):

私はもう結果を出しません-それはかなりかさばります。位相座標に移りましょう

 #    # Y[1] -> x(t) # Y[2] -> y(t) # Y[3] -> phi(t) # Y[4] -> vx(t) -     # Y[5] -> vy(t) -     # Y[6] -> omega(t) -    #            for i from 1 to s do N2 := subs(diff(q[i], t) = y[i+s], N2); N2 := subs(q[i] = y[i], N2); N1 := subs(diff(q[i], t) = y[i+s], N1); N1 := subs(q[i] = y[i], N1); F1 := subs(diff(q[i], t) = y[i+s], F1); F1 := subs(q[i] = y[i], F1); end do: #        for i from 1 to s do for j from 1 to s do eq := Main_EQs[j]; if has(eq, diff(diff(q[i], t), t)) then accel[i] := rhs(eq); end if; end do; for j from 1 to s do accel[i] := subs(diff(q[j], t) = y[j+s], accel[i]); accel[i] := subs(q[j] = y[j], accel[i]); end do: end do:

必要な力を計算するための関数を作成します

 #       GetN1 := proc(mass, length, grav_accel, fric_coeff, Y) local react := subs(m = mass, L = length, g = grav_accel, f = fric_coeff, N1); local i; for i from 1 to numelems(Y) do react := subs(y[i] = Y[i], react); end do: return evalf(react); end proc: #       GetN2 := proc(mass, length, grav_accel, fric_coeff, Y) local react := subs(m = mass, L = length, g = grav_accel, f = fric_coeff, N2); local i; for i from 1 to numelems(Y) do react := subs(y[i] = Y[i], react); end do: return evalf(react); end proc: #     GetF1 := proc(mass, length, grav_accel, fric_coeff, Y) local react := subs(m = mass, L = length, g = grav_accel, f = fric_coeff, F1); local i; for i from 1 to numelems(Y) do react := subs(y[i] = Y[i], react); end do: return evalf(react); end proc:

与えられたコードは膨大ですが、かなり単純です-数値パラメーターは対応する式とその計算に代入されます。一般化された加速度を計算するために同じ関数を形成します

 #     GetAccel := proc(mass, length, grav_accel, fric_force, normal_react, Y) local acc; local i, j; for i from 1 to numelems(Y)/2 do acc[i] := subs(m = mass, L = length, g = grav_accel, F = fric_force, N = normal_react, accel[i]); end do: for i from 1 to numelems(Y)/2 do for j from 1 to numelems(Y) do acc[i] := evalf(subs(y[j] = Y[j], acc[i])); end do: end do: return [seq(acc[i], i=1..numelems(Y)/2)]; end proc:

問題文で与えられたパラメータを設定します

 #    m1 := 2.0; L1 := 0.5; f1 := 0.1; g1 := 9.81;

摩擦力の計算を決定するモデルの基本ロジックを設定する時間。この場合、スライダーの速度の誤差を求めます。このとき、スライダーは速度がゼロであると想定します。

 #       GetFricNormal := proc(mass, length, grav_accel, fric_coeff, Y) local F1, N1; #      local eps_v := 1e-6; #     #    if abs(Y[4]) < eps_v then #        F1 := GetF1(mass, length, grav_accel, fric_coeff, Y); N1 := GetN1(mass, length, grav_accel, fric_coeff, Y); #       , #        if abs(F1) > fric_coeff*abs(N1) then F1 := fric_coeff*abs(N1)*signum(F1); end if; else #    ,       N1 := GetN2(mass, length, grav_accel, fric_coeff, Y); F1 := fric_coeff*abs(N1)*signum(Y[4]); end if; return [F1, N1]; end proc:

ソルバーのコールバックを定義します。

 #           (  ) EQs_func := proc(N, t, Y, dYdt) local F1, N1; #      local acc; #   local ret; #       ret := GetFricNormal(m1, L1, g1, f1, Y); F1 := ret[1]; N1 := ret[2]; #     acc := GetAccel(m1, L1, g1, F1, N1, Y); dYdt[1] := Y[4]; dYdt[2] := Y[5]; dYdt[3] := Y[6]; dYdt[4] := acc[1]; dYdt[5] := acc[2]; dYdt[6] := acc[3]; end proc:

ソルバーの位相座標と初期条件のリストを作成し（垂直角からのロッドの偏差角を小さくします）、数値積分を実行します（実際、最後のdsolve（）の呼び出しは、数値解法の意図を示しているだけで、位相座標の特定の値を計算するときに生成されます）。

 #    vars := [X(t), Y(t), Phi(t), Vx(t), Vy(t), Omega(t)]; #   initc := Array([0.0, 0.0, 1e-4, 0.0, 0.0, 0.0]); #   dsolv := dsolve(numeric, number = 6, procedure = EQs_func, start = 0, initial = initc, procvars = vars, output=listprocedure);

準備作業を実施します

 #      x := eval(X(t), dsolv); y := eval(Y(t), dsolv); phi := eval(Phi(t), dsolv); vx := eval(Vx(t), dsolv); vy := eval(Vy(t), dsolv); omega := eval(Omega(t), dsolv);

次に、特定の時間間隔でのシステムの動きを計算し、グラフに出力するためのデータ配列を作成します

 #         t0 := 0.0: t1 := 10.0: num_plots := 1000: dt := (t1 - t0)/num_plots: t := t0: i := 1: while t <= t1 do Time[i] := t; Y := [x(t), y(t), phi(t), vx(t), vy(t), omega(t)]; x1[i] := Y[1]; phi1[i] := Y[3]; fric[i] := GetFricNormal(m1, L1, g1, f1, Y)[1]; norm_react[i] := GetFricNormal(m1, L1, g1, f1, Y)[2]; lim_fric[i] := f1*abs(norm_react[i])*fric[i]/abs(fric[i]); t := t + dt; i := i + 1; end do:

まあ、ほとんどすべての準備ができています

 #   G_x := [ [Time[k],x1[k]] $k=1..num_plots]: G_phi := [ [Time[k],phi1[k]] $k=1..num_plots]: G_fric := [ [Time[k],fric[k]] $k=1..num_plots]: G_norm_react := [ [Time[k],norm_react[k]] $k=1..num_plots]: G_lim_fric := [ [Time[k],lim_fric[k]] $k=1..num_plots]: #     gr_opts := captionfont=['ROMAN', 16], axesfont=['ROMAN','ROMAN', 12],titlefont=['ROMAN', 14],gridlines=true: plot(G_x, gr_opts, view=[t0..t1, -1..1.0]); plot(G_phi, gr_opts, view=[t0..t1, 0.0..7.0]); plot({G_fric, G_lim_fric}, gr_opts, view=[t0..t1, -20..20]); plot(G_norm_react, gr_opts, view=[t0..t1, 0.0..200.0]);