親愛なる暗号作成者と数学者の皆さん!
暗号化アルゴリズムがどのように機能するかをすぐに理解することは、専門の数学者や暗号作成者ではなく、私にとって容易ではありません。 これは、1つのアルゴリズムの個々の機能を扱う試みです。 また、たとえばKeccakよりもSpritzアルゴリズムが専門家によって議論されるようになった理由を理解してください。 Habréには、 スポンジの機能 、またはロシア語ではスポンジ( 1、2 )について説明した記事がいくつかありました。 この関数は、いくつかの方法で使用できます:暗号化/復号化、ハッシュ、個別のドメインを持つハッシュとして、メッセージ認証コード(MAC)または挿入コードを生成、ストリーム暗号およびランダムアクセスのストリーム暗号として機能し、関連データ(認証済み)関連データによる暗号化)、擬似乱数ジェネレータとして、およびパスワードから対称キーを生成します。
理解するために、元の記事とプレゼンテーション 、およびGitHubのソースコード( C 、 JS )を使用しました。
私は専門家ではないので、例を使って理解し始めます。 特に、関数hash(M、r)を使用します。
Mは入力バイト配列です。
rは、バイト単位の配列の出力ハッシュの長さです。
この例からわかるように、入力配列の長さは3バイトで、出力は32バイトです。 したがって、配列の長さは29バイト増加します。
これがどのように起こるか見てみましょう。
最初に、変数と順列の配列が初期化されます。
i = j = k = z = a = 0;
wは1です。
i、jは2つの要素の位置です。
kがキーです
zは最後に計算された値です。
a-使用されるニブルの数(ニブル)
これらの値はすべてゼロであり、順列配列の初期値は1からNまでです。この例では、Nは256です。
w-ホップ幅は1ですが、Nの最大公約数の存在によって異なる場合があります。
吸い取る
次に、absorb(M)関数が呼び出されます-この例の配列Mが3バイトで構成されていることを思い出してください。 明確にするために、「A」、「B」、「C」というバイトにします。 スポンジのサイズは256バイトとかなり大きく、3バイトを吸収する必要があります。 各バイトに対して、「B」および「C」の場合と同様に、absorbByte(「A」)関数を呼び出します。
各バイトを2つのニブル(上位と最下位)に分割し、それぞれについて、aboveNibble関数(「下位4ビット」)を呼び出します。これは、バイトの上位4ビットについても同じです。
現在のニブルの吸収はどうですか? absorbNibble関数は、順列配列(1に等しい)から最初のバイトを取得し、配列の中央に等しい位置でそれを妨げます。
順列とニブル自体の値。 コードAは65なので、最低ニブルは1です。その後、最初の要素の新しい位置は128 + 1 = 129です。
そして、最初の位置には129という数字があります。
次に、使用済みニブルのカウンターを1つ増やします(a = 2)。
古いニブルと残りの2バイトについても同じことを行います。 この例では、使用するニブルの数に応じて、合計で6回の順列を実行する必要があります。
シャッフル
その後、shuffle()関数を実行します-shuffle。
これは次のようなものです。
/* Shuffle() 1 Whip(2N) 2 Crush() 3 Whip(2N) 4 Crush() 5 Whip(2N) 6 a=0 */ function shuffle() { whip(TWO_N); crush(); whip(TWO_N); crush(); whip(TWO_N); a = 0; }
最初のステップは、update()関数を実行することです-2N回更新します。 この関数では、SpritzがRC4( プレゼンテーション 、 分析 )と異なります。
RC4と操作を比較する
RC4:
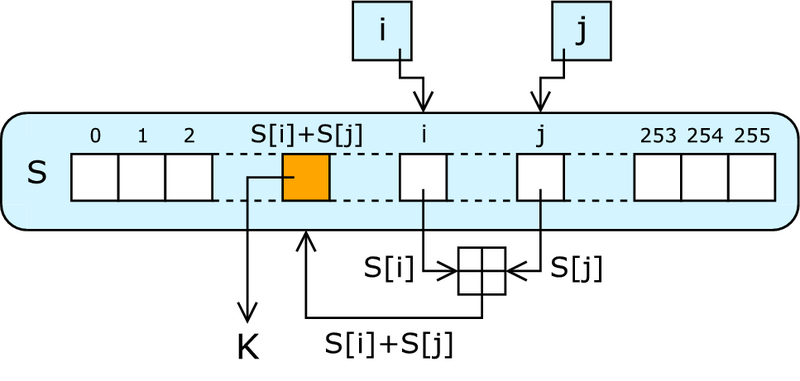
1: i = i + 1 2: j = j + S[i] 3: SWAP(S[i];S[j]) 4: z = S[S[i] + S[j]] 5: Return z
スプリッツ:
1: i = i + w 2: j = k + S[j + S[i]] 2a: k = i + k + S[j] 3: SWAP(S[i];S[j]) 4: z = S[j + S[i + S[z + k]]] 5: Return z
理解を深めるために私の修正を加えたSpritz:
1: i = i + w 2: j = j + S[i] 2a: j = k + S[j] 2b: k = i + j 3: SWAP(S[i];S[j]) 4a: i = i + S[k+z] // z=S[j] c 4b: j = j + S[i] 4c: z = S[j] 5: Return z
4、操作は次のように表すことができます:Ez = S [j + S [i + S [k + z]]] = kzpSipSjpS。
振ってつぶす
パラメーターwがありました-これは奇数でなければなりません。 RC4では、常に1です。
別の従属パラメーターkが現れました-キー。
ホイップ(2N)関数の名前は、シェイク、およびクラッシュ()クラッシュ方法として変換できます。
ホイップ機能は、操作1,2,2a、3を実行します。 次に、wとNの最大共通因子が見つかった回数だけパラメーターwを1増やします。
iは1から512までのすべての値を実行します。k= 0と仮定します。 したがって、初期化中に設定されます。 次に、最初の反復の前に、jは0に等しくなります。最初の反復の後、j = S [S [1]]ですが、S [1] = 129で、absorbで最初と129個の要素が一度だけ再配置された場合、j = 1です。 次に、ステップ2aのkは値k = 129を取ります。
Crush()関数は、右側の値が左側の値よりも大きい場合、順列の配列の中心に関して対称な値を変更します。
スクイーズ
これが最後のスクイーズ(r)操作です。 出力配列\ハッシュでは、rバイトを取得する必要があります。 drip()およびupdate()を呼び出した後、最終的な操作出力()が実行されます。
/* Output() 1 z = S[j+S[i+S[z+k]]] 2 return z */ function output() { z = S[ madd(j, S[ madd(i, S[ madd(z, k) ]) ]) ]; return z; }
ご覧のとおり、RC4とは異なり、この操作は前のステップで計算されたz値に依存します。 それはややフラクタルなアルゴリズムであることがわかります。
お知らせ
これは完全に新しい暗号であり、実際の分析が現れるまでの時間です。 コードを表示した結果、次の機能を使用しました。
/* addition modulo N */ function madd(a, b) { return (a + b) % N; // return (a + b) & 0xff; // when N = 256, 0xff = N - 1 } /* subtraction modulo N. assumes a and b are in N-value range */ function msub(a, b) { return madd(N, a - b); }
すべての加算と減算は、サイズNの循環バッファーで実行されます(これは記事で指定されています)。 これはおそらくこの特定の実装の機能ですが、単純な合計または差で十分なように思えました。 私が正しく理解していれば、バッファのサイズは異なる場合があります。
コードはwの初期値に敏感です。 初期化中、このパラメーターは1に設定されますが、Nに設定された場合はどうなりますか?
順列配列Sは1からNまでの値で初期化されます。したがって、入力バッファーの長さが小さい場合、S [i] = iになり、その後のラウンドでこれが真になります。
キーと初期化ベクトル(IV)の特別な選択により、一部の操作が大幅に簡素化される可能性があります。 そして、一般に代数的複雑さは低いでしょう。 たとえば、2aはj = k +(i + j)<< 1と同等です。
合計
暗号化に対する非常に興味深いアプローチがSpritzで開発されています。 私の意見では、既存の実装には大幅な改良が必要です。 また、この暗号が明らかになるかどうかは時間がかかります。 RC4よりも遅いことがすでにわかっています。 この暗号はパブリックドメインに配置されており、ライセンスの制限はありません。
Spritzは、AbsorbStop関数、暗号化、ハッシュ関数、ドメイン分離ハッシュ関数、メッセージ認証コード(MAC)、関連データによる認証暗号化(AEAD)、決定論的ランダムビットジェネレーター(DRBG)を実装するため、おそらく普及する可能性があります。 )
おそらく、これらの機能は、分散データベース、インターネットを介したオーディオやビデオの転送などに使用できます。
また、尊敬される専門家が満足している場合、次の記事を書くことができます。ここでは、AEADを使用して、特定の時間だけ機能するワンタイムデジタルキーを作成する方法を示します。 これは、特に、車、モーテル、ヨット、アパートのリモートレンタル、またはホテルやゲストハウスのIoT施設の管理に使用できます。
PSリンクについてはIvan_83に感謝します低代数的複雑さKeccak / Keyakはキュービック攻撃を促進します。