行列指数を計算しない方法

この投稿は、ユーザーpchelintsev_anの 投稿の影響を受けて作成されました。



この記事では、マトリックス指数を計算する「単純な」方法に沿って進むと、どのような計算上の困難が発生するかを説明します。 この記事は、計算数学に精通したいが、常微分方程式系やコーシー問題などの概念に既に精通している人には役立つかもしれません。 実験はGNU Octaveシステムを使用して実行されました。

一般的な行列指数とは何ですか？

定数係数を持つ常微分方程式の線形システムのコーシー問題を考慮すると、行列指数が発生します。







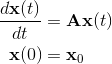
そのようなシステムは、たとえば有限要素法などで偏微分方程式を部分的に離散化した後に発生することがあります。 その場合、行列Aは微分演算子の有限次元近似です。 その結果、行列Aの行数は、数千、数百万、さらには数十億にも達する可能性があります。 このような行列は、正方配列の形式で保存することさえできないため、特別なスパースプレゼンテーション形式で保存されます。



ODEシステムのソリューションは、明示的に記述できます。







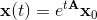
行列指数がここに表示されます。これは、シリーズの合計として定義されます。







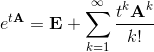
実際、行列指数は、行列Aをe ^zのテイラー級数に形式的に代入することによって取得されます（ 数学者は、級数が任意の行列および任意のtに対して絶対に収束することに気付くでしょう ）。 便利なことに、行列指数を使用して、いつでも解を計算できます。 たとえば、このシステムが、 AdamsやRunge-Kuttaなどの数値積分法によって解決される場合、費やされる時間は時間tに比例します。 ただし、行列指数による解決は、定数係数を持つ自律システムでのみ可能です。



行列指数の実際の計算のための微分方程式の過程で、行列をヨルダン型に縮小する方法が提案されます：行列AがSJS ^-1として表される場合、Jはジョルジュ型、Sはヨルダン基底への遷移行列、行列指数Aは行列指数Jで表されます：







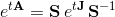
ヨルダン行列Jの行列指数は明示的に書き出されます。 ただし、この方法では、固有ベクトルのシステムとそれに固有のベクトルを計算する必要があります。 このタスクは、最初のタスクよりもはるかに複雑です。 さらに、実行列Aの場合でも、そのヨルダン型Jは複雑になる可能性があります。

行の合計

したがって、無限のシリーズがあり、予測可能な時間内にそれを計算したいという願望があります。 明らかな方法は、残りを破棄することにより、ある項の合計を終了することです。 さらに、ノルムの次のk番目の項が小さい場合、シリーズの合計は終了します。

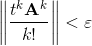
マトリックスノルム

マトリックスのノルムについて簡単に説明します。 さまざまなマトリックス標準があります。 要件に基づいてレートを入力できます





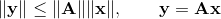
この場合、何らかのベクトルノルムに誘導される（または従属する）マトリックスのノルムについて話します。 最も使用されるベクトルノルムの場合、対応するマトリックスノルムの形式は次のとおりです。







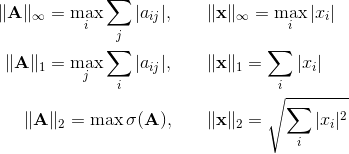
行列の最初の2つのノルムは初歩的なものと見なされ、最後に特異値を計算する必要があり、これは非常に困難です。 誘導された規範に加えて、他にも多くの規範があります。 フロベニウスのノルムは実際に便利であり、一方では計算が容易であり、他方では特異数Aと密接に関連しています。実際、これは行列を1つの行に「引く」ことによって得られるベクトルのユークリッドノルムです。

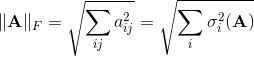
シリーズを要約するときの驚き

テイラー級数を合計するときに生じる困難を理解するために、行列指数を持つ例を参照する必要はありません。 同様に、間隔[ ^0、50 ]で関数e ^-xをプロットして、指数のテイラー級数を合計してみましょう。 次の項が10 ^-20を超えない場合、合計を完了します。 Octaveでは次のコードを使用します。

function [y] = myexp(x, eps) xk = ones(size(x)); y = xk; k = 0; do k = k + 1; xk = xk .* x / k; y = y + xk; until (max(abs(xk)) < eps) end x = linspace(0, 50, 2000); y = myexp(-x, 1e-20); plot(x, y, 'b', x, exp(-x), 'r'); axis([0 50 -0.1 1.1]);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

結果はかなり奇妙です：







x> 30の場合、関数グラフはランダムに動作し始め、指数とは関係ありません。



この効果の理由は、丸め誤差の蓄積です。 たとえば、e ^-35を計算すると、132の項が加算され、そのうち最後の項の最小値は絶対値s 132≈5.8674・10 ^-21で、項番号35の最大値は絶対値s 35≈-1.067・10 ¹⁴でした。 Octaveは倍精度（約16桁の有効数字）で計算を実行するため、35番目の項の丸めにより既に0.01のオーダーの誤差が導入されており、値ϵ = 10 ^-20とシリーズの合計値e -35≈6.305・10 ^-16の両方を大幅に超えています



テイラーのシリーズはとても絶望的ですか？ いいえ、合計された項がそのような大きな値に達しない場合、丸め誤差は重要な貢献をしません。 たとえば、このようなアルゴリズムは、xの小さな値（| x |≲1）に対して確実に機能します。 行列指数の場合、同様の条件の形式は 。 計算の安定性に加えて、このxの選択は高速な収束を提供します。つまり、許容可能な精度を得るには、系列からわずかな項のみを取得するだけで十分です。

引数倍増法

行列指数は次の関係を満たすことに注意してください。







これは、マトリックス指数がマトリックスに対して計算できることを意味します 、そして、結果をNの累乗にします。N= 2 ^pとして、p行列乗算で累乗する高速アルゴリズムを使用できます。

1. 行列指数を計算する
2. Bを自分で乗算する この操作をp回繰り返します
3. 結果として

数pは、アルゴリズムのステップ1の計算上の安定性の理由で選択できます（また、選択する必要があります）。





対応するオクターブコード：

 function [B] = taylorexp(t, A, eps, max_terms) B = eye(size(A)); Ak = B; k = 0; while norm(Ak, 'fro') > eps && k < max_terms k = k + 1; Ak = (t / k) * Ak * A; B = B + Ak; end end function [B] = argdbl(t, A, eps, max_terms) p = ceil(log2(abs(t) * norm(A, 'fro'))); B = taylorexp(t / pow2(p), A, eps, max_terms); for i = 1:p B = B * B; end; end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

パデ近似法

関数の値を近似的に計算する方法は、テイラー級数のセグメントだけではありません。 関数のより良い近似は、多項式の形式ではなく、有理関数の形式で取得できます。 与えられた次数の2つの多項式の比の形での最適な近似は、 パデ近似と呼ばれます 。 たとえば、指数の2つの2次多項式の比によるパデ近似は、次のように記述されます。







行列指数の同様の近似は次の形式になります。







パデ近似は、ダブリングアルゴリズムのステップ1に使用できます。 パデ近似に関連する主な問題は、マトリックスを1回反転させる必要があることです。 大きな行列の場合、これには非常に時間がかかります。

精度分析

行列指数が正しく計算されることを確認する方法は？ それで十分ですか または、より「スマート」なチェックが必要ですか？



行列の指数は青からではなく、常微分方程式系を解いた結果として生じたことを思い出してください。 行列Aの固有値は、この微分方程式系で記述される系で発生するプロセスの速度を特徴づけます。 たとえば、マトリックス：







1つの急速に減衰するプロセス（固有値-1000）と2つの振動プロセス（固有値± i ）を持つシステムを記述します。 行列指数を正しく計算するための適切な基準は、比率です。





行列Aの固有値とその行列指数を関連付ける。

計算実験

まず、さまざまなサイズのランダム行列のパフォーマンスアルゴリズムを調べます。 メソッドとして、テイラー級数を合計するメソッド、引数を2倍にするメソッド、およびOctaveに組み込まれているexpm関数を使用します。 当初、固有値の対応も比較したかったのですが、3つのアルゴリズムすべてが行列N≳50のサイズでこのチェックに等しく失敗したため、この考えを放棄しなければなりませんでした。これらの行列の値。







グラフに基づいて、2倍法はライブラリ関数の約2倍の長さで機能します（過大評価された精度要件を緩和する価値があるかもしれません）が、直接加算には異なる漸近的挙動≈O（N ^3.7 ）があり、残りは漸近的挙動O（N ³ ）。





次に、アルゴリズムが大きな固有値でどのように機能するかを確認しましょう。 次の常微分方程式系を考えます：





初期状態では：



。



その特徴は、その固有値の1つが-1000（急速に減衰する解）であり、他の2つが±i√2（振動解）であることです。 歪みが虚数固有値に導入される場合、これははっきりと見えるでしょう。 時間ステップτ= 0.038を取り、行列指数を見つける さまざまな方法で。 τのステップを持つグリッド上のシステムの解は、次の簡単なアルゴリズムによって取得されます。

1. 最初の瞬間の解は、初期条件からわかっています
2. 瞬間t _nでの解u _nがわかると、瞬間t _{n + 1} = t _n +τでの解は、行列指数Bを乗算することにより得られます。
   
   
   
   
   
   
3. 統合セグメントの終わりに達するまで、2番目のポイントを繰り返します。

得られた数値軌跡を見てみましょう（ベクトルの最初のコンポーネントのみが表示されます）。







すべての軌跡は、テイラー級数の直接合計によって得られたものを除き、視覚的に一致します。 グラフは初期条件x ₁ （0）= ₁を超えないことに注意してください。実際、グラフは指数y = 1に指数関数的に近づきます。グラフの「回転」の特性距離（〜1/1000）はタイムステップτ= 0.038。







この例は合成であると言えますが、実際には見つかりませんが、そうではありません。 固有値（実際には、物理​​的プロセスの速度）の強いばらつきを特徴とする、いわゆる剛体コーシー問題が数多くあります。

さらに読む

行列指数を計算するさまざまな方法は、記事[英語] [2]に記載されています。 注目すべき2巻の本が、常微分方程式とスティッフな問題を解く方法について書かれています[3,4]

使用されたソースのリスト

1. フェドレンコR.P. 計算物理学の紹介。 M。：モスクワ出版社。 物理的および技術的 協会、1994年-528s。 §17
2. Cleve MolerとCharles Van Loan 、25年後のマトリックスの指数関数を計算する19の疑わしい方法 // SIAM Rev. 45（1）、3–49。 （47ページ）
3. Hyrer E.、Nersett S.、Wanner G.常微分方程式の解。 厳格なタスク。 M。：世界、
   
   1990 .-- 512秒
4. Khairer E.、Wanner G.常微分方程式の解。 剛体および微分代数の問題。 M。：ミール、1999 .-- 685 p。