さまざまな目的のための衛星システムの弾道特性の設計と計算、運動と動作のプロセスのモデリングには、そのようなシステムによって計画された目標効果を達成する可能性の予備評価が必要です。 現在、その目的は、人工衛星(AES)の機器に搭載された最も広い意味のターゲットオブジェクト(CO)の情報サービスに限定されています。 情報が流れる場所では、情報の保護と情報セキュリティの確保に関連する問題が常に発生し、その後の結果がすべて生じます。
長い自律機能により、弾道特性、特に衛星システムの構造の設計値が変更されます。 また、これには、システム特性の一部の値の定期的な修正が必要です。 この場合、システムの個々の衛星とシステム全体の両方について、運動パラメータの測定値が利用可能であれば、それらの予備計算が必要です。 このような測定は、適切な測定機器とコマンド無線設備を備えた、固定式または移動式(陸上、海、空)の地上測定ポイント(IP)のネットワークが存在する場合に可能です。 ここでは、衛星システムの潜在的な能力を評価および計算して、軌道部分の弾道構造および地上部分の主に測定ポイントのオブジェクトの配置の観点から、地球規模の情報サポートに影響を与える確率的アプローチを検討します。 情報セキュリティの問題は考慮されません。
空間領域(インスタントサービスエリア(MLO))は、個々の起業家とセントラルヒーティングセンターに関連付けられており、衛星がこの衛星に入ると、サービスまたはセントラルヒーティングサービス自体を実行できます。 サービスプロセスには、弾道特性と遠隔測定特性の直接測定に加えて、ターゲット情報の受信、送信、衛星との通信、機内での修正プログラムの転送、搭載された特殊機器(BSpA)の動作の作業プログラム(RP)の集計、更新された移動パラメーターおよびその他の動作が含まれます。
先験的に、必要な推定値を取得するプロセスを確定的に決定することはできません。これは、多様な自然および技術的要因の作用がパラメータの摂動につながるためです。 まず第一に、衛星の運動のパラメータ、およびその結果としてのBSAAの機能の特性は外乱を受けやすい。 したがって、ランダムなイベント、量、ランダムな引数の関数およびランダムな関数(フィールド)の分布の確率的法則を確立するために、名前付き現象をランダムとして研究する必要が生じます。
読者の注意を引く作業では、システムの軌道部分と地上部分の関節運動と機能のモデルの枠組みの中で、AES-IPオブジェクトのペアの相互作用が考慮されます。 さらに、モデルには、機能プロセスを形成し、重要なシステムイベントの開始のランダム性を生成するすべての主要な要因が含まれます。 多くのシステムイベントのうち、衛星と地上IPおよびターゲットオブジェクトとの相互作用のイベントが区別されます。
システムモーションの数学モデルで考慮される最も重要な要素には、次のものがあります。
-軸の周りの惑星の回転(角速度定数);
-地上オブジェクトの地理的位置(座標、MLOの半径);
-対話セッションの限られた時間(MLO内のオブジェクトが費やした時間);
-衛星の弾道特性(飛行高度H、軌道面の傾斜)。
数学モデルでは、単純化された仮定と仮定が使用されます(導入されます)。
-惑星は球体Rの半径を持つ球形で、引力の重力場は中心です。
-軌道オブジェクトの動きに対する大気の影響は考慮されていません。
-衛星の運動軌道-円形、運動軌道の面の歳差運動は考慮されません。
-衛星の運動経路は、球の大きな円でモデル化されています。
-MLOサービスエリア—オブジェクトの中心に頂点をもつ円錐。半径R + Hの球との交線は、平らな円で惑星の球の表面に投影されます。
衛星の基礎– IP相互作用モデルは、システム要素の幾何学的モデルと、その動きの運動学的関係です。 平面の3次元空間では、システムの各衛星の軌道は動かず、惑星の球体との交線が経路になります。 地上の物体のMLO(半径R + Hの球と円錐の交線の惑星への投影)は、平面Kで切断された球面のセグメントに制限されます。MLO境界は、地球の表面に「描かれ」、地球とともに移動します。 衛星の軌道P平面と周期的に交差します。 MLOセグメントはルートと交差します。ルートは、衛星の各ラウンドで再び地球の表面に「描画」されます。 いくつかのターンで、トラックはセグメントを横断し、一部でそれを通過せずに通過します。 エントリポイントから出口ポイントまで、セグメントを横断するターンでのトレースの部分は、セグメント内にあります。 事実、衛星による1軌道の経路の通過にかかる時間は、1日の長さの15-16倍、つまり約1.5時間です。 パスがセグメントを横断する場合、衛星がMLOに留まる時間τは、円コードLの長さtに比例します( τ = t /2πR)。
実際、SPの測定器のアンテナは、回転して、ゾーンに入った瞬間からゾーンを離れるまで移動中の衛星に付随します。
問題の内容説明
タスクは次のとおりです。 衛星の軌道の平面PがMLO中心に対してランダムな位置でMLOセグメントを切断する可能性を決定します。
モデルの明確さと推論の利便性のために、2つの座標系を導入します。デカルト座標と球面(極座標)で、その始まりは球面惑星の中心と互換性があります。 球座標系の点O1の球上の位置は、3つの座標によって決定されます。
-ベクトルRの半径の長さ;
-経度λ;
-極距離γ=π/ 2-φ。
座標参照の正の方向を図に示します。 1。
デカルト座標系の軸oX、oyは惑星の赤道面にあり、oX軸はグリニッジ子午線との交点と一致し、oy軸はλ=π/ 2回転し、東経λ=π/ 2で子午線を通過し、oz軸はシステムを補完します適切なシステムに調整します。 球面座標からデカルト座標へ、またはその逆への遷移式は次のとおりです。
x =Rcosφcoscoslo; y =Rcosφosinin®; zはRsinφoです。
R = [x 2 + y 2 + z 2 ] o.5 ; λo= arctan y / x; φ= arctan z /√(x 2 + y 2 )。
デカルト座標系では、惑星球上のセグメントを形成する平面Kの方程式は、次のように定義できます。
Ax + By + Cz + D = 0、
ここで、A、B、Cは、平面K、D≠0に垂直なベクトルn <3>の成分です。
平面Kに垂直なベクトルn <3> = <A、B、C>の方向余弦は、式によって決定されます。
cos(α)= A / N; cos(β)= B / N; cos(γ)= C / N; N = [A 2 + B 2 + C 2 ] o.5 ; p = D / N、
ここで、pは原点から平面までの距離であり、符号(N)= –符号(D)です。
中心の位置に加えて、円Lを境界として持つセグメントの特性は、円Lの半径rです。この半径は、球の半径Rと距離(p)によって決定できます。
r =Rζc、ここでζc= arccos(p / R)。
言い換えると、球上のセグメントは、点O1(x、y、z)の座標-セグメントの中心と角度ζc、または点O1(x、y、z)と距離pの座標、またはシステム:球の方程式と平面Kの方程式によって定義できます。
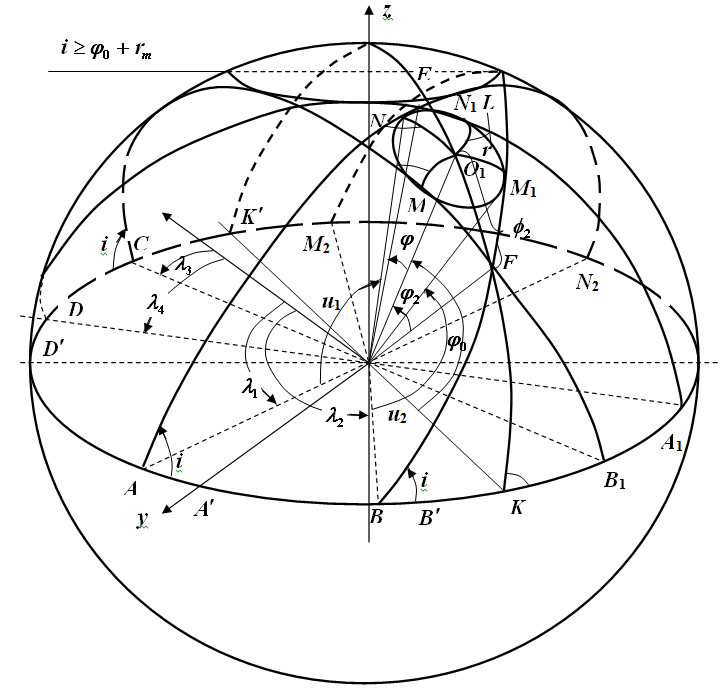
図1傾斜角iがMLO IPの境界の上部ポイントの緯度よりも大きい衛星軌道の位置
球の中心を通る平面は、同様の方法で定義できます。つまり、平面の一般方程式
A1x + B1y + C1z + D1 = 0
明らかに、プレーンの場合、値D1 = 0です。このプレーンをモデリングするためのより便利な方法があります。 一般的な場合、平面は、地球の赤道面に対して傾斜しています。これは、衛星の軌道の傾斜と呼ばれる特定の角度iで水平座標面と一致しています。 軌道Pの平面と水平座標hou平面の交線は、軌道のノードの行(昇順および降順)と呼ばれます。
赤道面におけるこの線の位置は、グリニッジ子午線から測定される角度λ(地理的経度)によって決まります。 任意の時点で、ある衛星の軌道のノードのラインは、角度λのランダムな値によって特徴付けられます。 明らかに、λの可能な値の範囲は、間隔λ∊ [0、2π]によって決まります。 この間隔内の任意の時点で、衛星軌道ノードが占有している他のすべてのノードに比べて高い優先度を持つポイントを指定することはできません。 これには物理的、数学的、またはその他の正当化はありません。 したがって、区間[0、2π]の軌道ノードのラインの経度λのランダム値の確率分布は均一であると仮定します。
赤道面に対する軌道面の傾斜角iは、非ランダムと見なされます。 このような状況では、平面P(i、λ)が次の形式でこれらの角度を介した表現を使用する方が便利です。
x•tgλ-y + z•ctgi /cosλ= 0。
ランダム変数λの可能な値の1つは、衛星P(i、λ)の軌道面の空間内の各ランダム位置に対応します。
地上の測定ポイントのゾーンの衛星による通過
衛星システムの設計者にとっての実際的な関心は、軌道の各ターンで衛星およびIP通信セッションを行う可能性を評価することです。
longitudeによって、ランダムな経度λの場合、惑星の球の中心を通る平面(i、λ)が点1(x、の半径ベクトルを中心とする円Lで囲まれたセグメントと交差するという事実から成るランダムな複合イベントを示します。 、z)。 したがって、作業のこの部分では、タスクはランダムイベントoccurrenceの発生確率を決定することです。 λがその可能な値の1つを取る場合、確率決定が実行されます。 課された条件が常に満たされることは明らかです。 確率理論の方法により、特定の方法で関連し、何らかの方法で確率が与えられたり決定されたりする他のイベントの既知の確率を通じて、いくつかのイベント(複雑な)の確率を決定できます。
イベントimplementingを実装する可能性を分析しましょう。 図1は、シミュレートされたランダムイベントoccurrenceの発生を助長する以前に考慮されたオブジェクトのさまざまな状況のジオメトリを示し、その発生が不可能な条件を示しています。
図1は、惑星の上半球を示し、大小の円弧が描かれています。 閉曲線MNN1M1は、MLOセグメント(円L)の境界を表します。 セグメントO1(x、y、z)の中心の位置は、緯度角度φoと経度角度λoによって特徴付けられます。 平面P(i、λ)の位置は、赤道の平面に対する傾斜角iによって決まります。この角度は、シミュレーション中に決定され、変化しません。
ランダムイベントの考えられる状況の分析 ℬ。
複雑なランダムイベントを生成するさまざまな機能的依存関係につながる状況を区別しますℬ:
最初の状況は、 φo+ r m≤iです。 4つの点N、M1でセグメントの境界(円L)に接する平面の位置に対応するλの4つの値に対して、平面(i、λ)による球の断面によって形成される大きな円ANN2、BM1M2、CMB1、DN1A1の円弧の4つの位置があります、N1、M。円弧KO1K1は、子午線断面のhoの平面に垂直で、z軸と点O1を通る平面による球の断面によって形成されます。
惑星の球体のセクションで、houの赤道面は上記の面の節の線を示します。
角度も表示されます:
-u1、u2-ノードの線と、円弧Lと円弧Bによってそれぞれ測定された、円Lの接線のポイントへの方向の間。
-φ1、φ2-子午線断面の円弧O1EおよびO1Fで測定された、セグメントの中心の半径ベクトルと大きな円の交点への方向の間。
-i-ハウの平面に対する平面P(i、λ)の傾斜角。
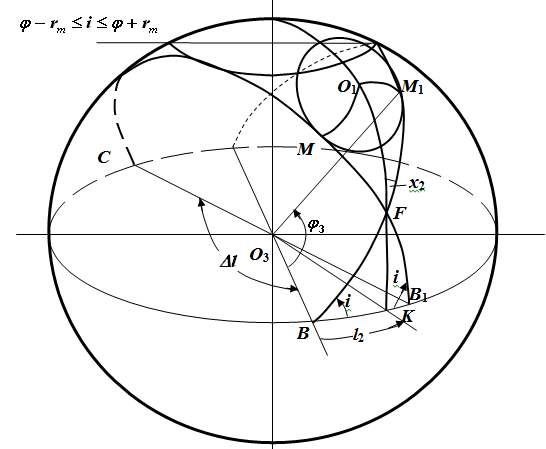
図2傾斜角iがMLO IPの境界の上部ポイントの緯度よりも小さい衛星軌道の位置
2番目の状況は、 φo-r m≤i≤φo+ r mです。 次の図2は、点MとM1での円Lへの接線に対応するλの2つの値に対する平面(i、λ)の2つの位置を示しています。
図の分析に基づいて、ランダムイベントrealの実現は、上の図1の赤道円の2つの間隔ABとCD、および下の図2のCBの1つの間隔で、平面P(i、λ)の節点に対応すると結論付けることができます。
上の図は、平面の傾斜角iの変化の間隔に対応しています
φ+ζc≤i≤π-φ-ζc、
下の図は、φo-ζc≤i≤φo+ζcです。
間隔ABおよびCD(下の図CB)は、平面P(i、λ) がセグメントに当たる間隔 、または要するにそれらの間の間隔と呼ばれます 。 セグメントの各固定位置とサイズζcおよび平面の傾斜角(i、λ)に対して、一意に決定されたヒット間隔があります。 位置、サイズ、ヒット間隔の数は、角度i、セグメントの中心の座標(φ®、λ®)、およびセグメントの半径ζcに依存します。
分析から、ランダムイベントtheは複雑であり、ランダム値λは上図の状況では間隔ABおよびCDに、下図の状況では間隔CBに属するという事実からなる、ランダムな単純なイベントで表すことができます。
3番目の状況は、 φo-r m > iです。 この状況は、ランダムイベントoccurrenceの発生に対応しないため、作業では考慮されません。 衛星の運動面は赤道上で非常に低く傾斜しているため、オブジェクトのMLOは赤道と交差できません。
複雑なランダムイベントの表現random単純なランダムイベント 。
not1 =(λ∊ ﺭ AB)とℬ2=(λ∊ ﺭ CD)の表記法を導入し、次にℬ=ℬ1+ ation2を表記します。 イベントℬ1とℬ2は互換性がないため、ノードλの経度の分布則がわかっている場合、P(ℬ)= P(ℬ1)+(ℬ2)の関係が満たされます。
houの平面内の大きな円にわたる確率変数λの確率分布、すなわち 区間[ 0、2π ]では、ノードの経度の連続関数によって与えられます-確率分布密度
φλ(λ)= dFλ(λ)/dλ、ここでFλ(λ)はλの分布関数です。
2つのアークが境界点A、BおよびC、Dによって数値軸λでマークされている場合、アークABおよびCDの間隔でλが得られる確率は次のように記述されます。

P(ℬ1)=∫φλ(λ)dλ; P(ℬ2)=∫φλ(λ)dλは、これらの示された制限の積分によって決定されるため、
P(ℬ)=∫φλ(λ)dλ+∫φλ(λ)dλ、ここで積分限界の値はまだ決定されていません。 したがって、確率P(ℬ)を決定するには、アークの長さλjによって特徴付けられる区間の境界の式を取得する必要があります。j= 1(1)4。 λj=λj(R、φ、λ、i、ζc)、j = 1(1)4。 ヒット間隔の長さの明示的な式を見つけます。
図1の分析に戻ります。その検討から、次のように書くことができます(arc ﺭ DDの表記を使用します)。
λ1=λA=λo-ﺭ AK; λ2=λ=λ-ﺭ VK; λ3=λ=λ- π + ﺭ VK; λ4=λD=λ- π + ﺭ AK。
数値計算を実行するための比率
球面三角法の定理を使用して、必要な変数の計算式を取得します。
ここで、アークは長方形の球面三角形AEKおよびBFKから決定されます。
AK = arcsin(tg(φ+φ1)/ tgi); BK BK = arcsin(tg(φ-φ2)/ tgi)。
未知の量φ2、φ1、λj=λj(R、φ、λ、i、ζc)、j = 1(1)4は、既知のφ、i、ζcによって決定されます。
球面三角形NEO1から正弦定理により、次の関係を書くことができます。
sinζc/ sind = sinφ1/ sin90°、ここで角度d =ےNEO1から、関係式からsind = sinζc/ sinφ1が得られます。
球面三角形AEKの余弦定理により、次の関係を記述します。
cosi = sindcos(φ+φ1)。これから、sindに対して別の依存関係sind = cosi / cos(φ+φ1)が得られます。
異なる方法で見つかった2つの依存関係を等しくし、変換を実行します(変数φ1の関数を左に転送します)
sinζc/ sinφ1= cosi / cos(φ+φ1)またはcos(φ+φ1)/ sinφ1= cosi / sinζc。
最後の式では、未知の変数φ1のみが既知の量を介してバインドできたため、変換が実行され、計算に便利な形式に縮小されます。
cos(φ+φ1)/ sinφ1= cosφctgφ1-sinφおよびさらにcosφctgφ1-sinφ= cosi / sinζcwhence
ctgφ1=(cosi / sinζc+sinφ®)/cosφ®そして最後に、
φ1= arctg(cosφ®sinζc/(cosi +sinφsinζc))。
類推により、球面三角形OMFとBFKを考慮して、値を取得します
φ2= arctg(cosφ®sinζc/(cosi-sinφsinζc))。
得られたφ1とφ2の値を経度の関係λjに代入すると、j = 1(1)4、
λ1=λA=λ-arcsin(tg(φ+ arctg(cosφsinζc/(cosi +sinφosinζc)))/ tgi);
λ2=λB=λ-arcsin(tg(φ-arctg(cosφsinζc/(cosi-sinφsinζc)))/ tgi);
λ3=λC=λ-π+ arcsin(tg(φ-arctg(cosφsinζc/(cosi-sinφsinζc)))/ tgi);
λ4=λD=λ-π+ arcsin(tg(φ+ arctg(cosφsinζc/(cosi +sinφsinζc)))/ tgi)
したがって、確率P(ℬ)の計算に必要なすべてのデータが定義されています。
例を考えてみましょう。 アプリケーションでは、経度の分布の法則λjが区間[0、2π]で均一であることが受け入れられます。 この仮定の下で、確率変数λの分布関数Fλ (λ)および分布密度φλ(λ)は、図3に示す形式で記述されます。
これらの分布則の数値特性は、次の式から決定されます。期待値m(λ)=π; 標準偏差シグマ(λ)=π/√3; 分散D(λ)=π2/3。 ( )
(ℬ)=∫φ λ (λ)dλ +∫φ λ (λ)dλ =1/2π ∑|λ 2j — λ 2j–1 |, j = 1,2.
λj,
(ℬ) = 1/π ∑(-1) k arcsin(tg(φ –(-1) k arctg(cos φ sin ζc /(cosi –(-1) k sinφsin ζc))) /tgi), k = 1,2.
この比率により、衛星が地上局のサービスエリアを通過したという事実から、システムの動きの数値特性(IPゾーンに転じる軌道の上昇ノードの経度の位置)に応じて、衛星が駅のゾーンにとどまる問題の解決策に移行できます。著者による研究のこの部分は、近い将来出版される予定です。