子どもたちの質問は通常非常に複雑です(「夜空が暗いのはなぜですか?」、「なぜりんごが地面に落ちるのですか?」)。 そして、大人が常にこれらの質問に対する答えを知っているとは限りません。
しかし、ゼロで割るという問題は決して複雑な問題の1つではなく、私にとってこれほど多くの問題が発生する理由は謎のままです。 恐らくこれは、算数の研究からアルファベット代数の研究への移行の困難さと初等関数の性質における、高校で数学を教える方法論のいくつかの欠陥によるものです。
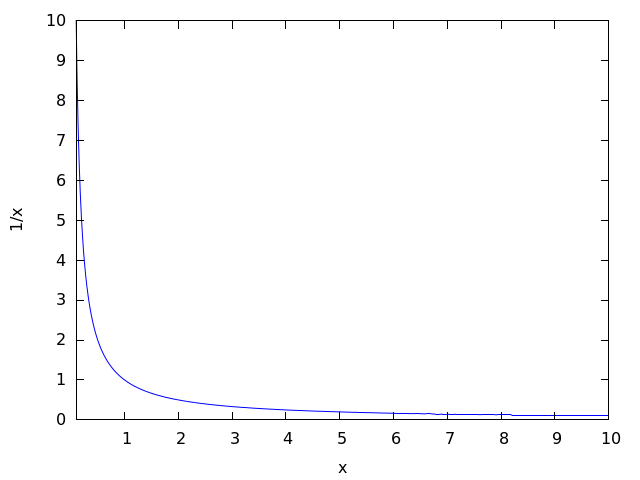
最も深刻な疑問は、有理数を研究した後、ゼロを除く任意の数xについて、逆数1 / xの概念が導入され、双曲線y(x)= 1 / xのグラフが生じると思います。
明らかに、1を非常に小さな数で除算すると、非常に大きな数が表示され、xを小さくするほど1 / xが大きくなります。 なぜ1 / x =∞と言えないのか-なんらかの数字がありますか?
これに対する代数的反対は次のとおりです。 ∞= 1 / xが数値であると仮定します。 次に、通常の番号に適用されるすべてのルールがこの番号に適用される必要があります。 特に、一方では関係0⋅∞= 1が真でなければならず、他方では0 = 1−1なので、0⋅∞=1⋅∞−1⋅∞= 0が満たされなければなりません。 したがって、1 = 0であり、このことから、すべての数値が互いに等しく、ゼロに等しいことがすでにわかります。 実際、1⋅x= xは任意の数xに対して真であるため、1⋅x=0⋅x= 0です。
「まあ、それは完全なナンセンスではないのですか?」私たちはこの場所に着くと自分自身に尋ねます。
もちろん、普通の数字について話しているのであれば、これはまったくナンセンスです。 しかし、理由なく、上記の「ルール」という言葉を強調しました。 ゼロ除算に対する算術的な異議を考慮した後、少し後でそれらに戻ります。Beanはこれに役立ちます。
コンピューター、計算機、または対数定規がなかった時代に戻り、乱数を5で割るタスクを自分で設定しましょう。
これを行うには、自然の列を象徴する豆の入ったボウルを用意し、そこからいくつかの量の穀物を紙のシートに注ぎます:

したがって、Bean計算機に配当を設定します。
課題は、これらの粒子を5行に配置することです。 混乱しないように、これらのシリーズに注意してください。つまり、除数を設定します。
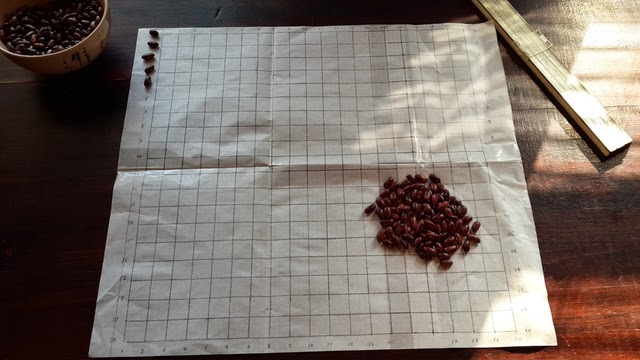
次に、ヒープのグレインを列の5行にレイアウトします。 これは、従来の計算機よりもはるかに長くなりますが、位置番号システムが発明される前に算術の美しさを感じることができます。

アルゴリズムは、長方形の数と(おそらく)残りを取得すると終了します。

この例では、2つのグレインが残り、5つのグレインの列がそれぞれ18を形成しました。乱数は18⋅5+ 2 = 92でした。
ゼロ以外の自然な割り切れる数と自然な除数に対してこのアルゴリズムを実行できることは明らかです。 除数が0の場合、このアルゴリズムは実行不可能です。
「待って!」気配りのある読者が言うでしょう。 -「検討した例では、残りの2を取得しました。これをどうしますか?」
これは実際、非常に重要なポイントです。 一般的に言えば、Bean計算機を破壊せずにBeanを分割することはできません。2つのBeanを5つの同一の部分に分割するのが難しいだけでなく、適切に分割しても収集できません。
したがって、長い間人々は端数なしでやろうとしました。 たとえば、12世紀の匿名のアラビア語の原稿では、次のタスクが説明されています。「100ポンドを11人に分ける」。 100 =11⋅9+ 1なので、中世の数学者は、最初に9ポンドを全員に与え、次に残りのポンドを卵と交換することを提案します。科学者は、8個の卵のそれぞれに配布し、残りの3個の卵をセクションの作成者に提供するか、卵の塩と交換することを提案します。
現代の数学言語では、分割は自然数の半円で行われました。 ただし、赤と白の豆を使用して同じように成功すると、剰余と整数のリングで除算を定義できます-説明したアルゴリズムでは、豆の粒の計算に使用する色を選択するための追加のルールが表示されますが、操作は無意味のままですタイプx / 0および5/2。
明らかに、5/2シンボルに特定の意味を与えるには、ゲームのルールを変更し、 合理的な分数のフィールドに移動して 、整数のセットにすべての種類の式m / nを追加する必要があります(mは整数で、nは整数です)。
これは唯一の方法で行うことはできないことに注意することが重要ですが、古典的な算術では、シンボル1 / nが1をnで除算する割合、つまり式n⋅1/ n = 1; さらに、ピースオブジェクト(たとえば、豆粒)をカウントする場合、シェアは意味がありませんが、連続的(または少なくとも無限に割り切れる)であると想定される数量-セグメントの長さ、数字の正方形など
有理数分数の分野では、ゼロ以外の除数の商は何らかの有理数分数であるため、部分商と剰余を考慮することはもはや意味がありません。 さらに、自然数の場合と同様に、アルゴリズムを変更せずにBeanを分割に使用できます。
実際、有理数α= p / qをβ= r / sで割る必要があります。 これは、次を実行することと同等です。
α:β= p / q:r / s =p⋅s/q⋅r
そして、有理αとβの問題は、整数を分割するための既知の手順に還元されます。 これもまた、ゼロによる除算には算術的な意味がないことを示しています。
「本当に除算したい場合でも、ゼロで除算することは不可能ですか?」-残念ながら、この質問に対する答えは肯定的です:カウントと測定の自然なニーズに基づいてゼロ除算の動作を決定することはできません。 確かに、2つの抜け穴があります。
最初:「通常の」数字(つまり、自然数の輪と有理数の場、実数の場の代わりに、ちなみに私はまだ言葉を言わず、いつかあなたに伝えます)、退化した場合を考えます-自明な環{0}であり、定義により0/0 = 0です。 この場合、「すべての数字は互いに等しく、ゼロに等しい!」と言われたとき、落ち着いた口調で言うことができます。 いつもそうだった。」
第二:おなじみの乗算の規則を放棄します。 特に、公理0⋅x= 0から。 彼らはこれが可能であると言います( http://en.wikipedia.org/wiki/Wheel_theoryを参照)。 もちろん、このオプションは最初のオプションよりもはるかに興味深いものですが、ゲームのルールにこのような変更が加えられたため、古典的な算術の枠組みをすぐに超えてしまいます。
このメモの終わりに、数字システムに興味のある人のための参考文献のリストを提供したいと思います。
-I.V. アーノルドの「理論算術」、M、OGIZ 1938-四元数を含む古典的な数値システムの説明を見つけることができる非常に詳細で詳細な本。
-EG Gonin“ Theoretical Arithmetic”、M、1959 —この本は短く、より現代的で、非常に優れていますが、I.V。の本ほど詳細ではありません。 アーノルド。
-S.フェファーマン「数値システム」-古典的なモノグラフ、時には非常に複雑。 理論的算術に関する他の2冊の本には見られない特定の質問がいくつかあります。
-A. A.キリロフ「数字とは」 (1993)-訓練を受けた読者向けにデザインされた小さなパンフレット。
-E. B.ダイキン、V。A.ウスペンスキー「数学的会話」は小学生に人気のある本です。 p進数字などの「非標準」トピックに関する多くの情報とタスクが含まれています。