Clever Geek Handbook

ハードODEの数値解法に利用可能なライブラリの概要





国内の数学プログラムSMath Studioに追加を作成すると、ネットワーク上で、自分のプログラムで使用できるライブラリがいくつか見つかりました。 それらの簡単な概要を提供します。



固定ピッチの標準RK45はほとんどの場合に役立ちますが、これでは不十分なタスクがあります。 リジッドシステムを解決するために、特別なソルバーが考案されました。これを実用的な観点から検討します。



以下の関数のほとんどは、特に明記しない限り、単一の呼び出し形式に縮小できます（Mathcadと同様）。 



ode_solver( init, x1, x2, intvls, D(t, x) )


ここで：



1. Intel ODE Solversライブラリ



次の関数が含まれています：rkm9st（）、mk52lfn（）、mk52lfa（）、rkm9mkn（）、rkm9mka（）。





ライブラリは、すべての依存関係とともにCで記述されています。 32ビットおよび64ビットバージョンのライブラリが利用可能です（libiode_ia32.libおよびlibiode_intel64.lib）。



intel_ode.h 
 /******************************************************************************* ! INTEL CONFIDENTIAL ! Copyright(C) 2007-2008 Intel Corporation. All Rights Reserved. ! The source code contained or described herein and all documents related to ! the source code ("Material") are owned by Intel Corporation or its suppliers ! or licensors. Title to the Material remains with Intel Corporation or its ! suppliers and licensors. The Material contains trade secrets and proprietary ! and confidential information of Intel or its suppliers and licensors. The ! Material is protected by worldwide copyright and trade secret laws and ! treaty provisions. No part of the Material may be used, copied, reproduced, ! modified, published, uploaded, posted, transmitted, distributed or disclosed ! in any way without Intel's prior express written permission. ! No license under any patent, copyright, trade secret or other intellectual ! property right is granted to or conferred upon you by disclosure or delivery ! of the Materials, either expressly, by implication, inducement, estoppel or ! otherwise. Any license under such intellectual property rights must be ! express and approved by Intel in writing. ! !****************************************************************************** ! ! Header file for Intel(R) ODE Solvers ! !*******************************************************************************/ #ifndef _INTEL_ODE_H_ #define _INTEL_ODE_H_ #ifdef __cplusplus extern "C" { #endif /* __cplusplus */ void dodesol(int*,int*,double*,double*,double*,void*,void*,\ double*,double*,double*,double*,double*,int*,int*); void dodesol_rkm9st(int*,int*,double*,double*,double*,void*,\ double*,double*,double*,double*,double*,int*); void dodesol_mk52lfn(int*,int*,double*,double*,double*,void*,\ double*,double*,double*,double*,double*,int*,int*); void dodesol_mk52lfa(int*,int*,double*,double*,double*,void*,void*,\ double*,double*,double*,double*,double*,int*,int*); void dodesol_rkm9mkn(int*,int*,double*,double*,double*,void*,\ double*,double*,double*,double*,double*,int*,int*); void dodesol_rkm9mka(int*,int*,double*,double*,double*,void*,void*,\ double*,double*,double*,double*,double*,int*,int*); #ifdef __cplusplus } #endif /* __cplusplus */ #endif /* _INTEL_ODE_H_ */


ODE Solversアドオンは、c＃コードからこのライブラリを操作する方法を示しています。



参照：

1. インテル®常微分方程式ソルバーライブラリ 。

2. ODESolversアドオンのソース。



2. GNU科学ライブラリ（GSL）



次の関数が含まれています：rk2（）、rk4（）、rkf45（）、rkck（）、rk8pd（）、rk1imp（）、rk2imp（）、rk4imp（）、bsimp（）、msadams（）、msbdf（）



それらのいくつかは、仕事のために追加のパラメーターを必要とします（ヤコビアン）。 私が何とか一般的な見方をすることができたもの：



非剛性システムのソルバー：





残り：





ユニバーサルインターフェイスは 、特定のタイプのソルバーがステップ関数を定義する関数を操作するために使用されます。 GNUScientificLibraryアドオンは 、c＃コードからこのライブラリを操作する方法を示しています。



Windowsでライブラリを構築するのはそれほど簡単ではありません。 現在利用できないサイトからの指示を使用しました。 ただし、アドオンリポジトリには、GSL 1.16の32ビットバージョンと64ビットバージョンのdll libがあります。 ODEソルバーだけでなく、ライブラリ全体があります。



参照：

1. GSL。 常微分方程式 。

2. GNUScientificLibraryアドオンのソース。



3. Matlab C ++ Math Library 2.1（Win32）



はい、この古いバージョンのランタイムライブラリを計算に使用できます。 さらに、相対パスによって確立できます。 元の配布キットの内容（拡張形式で最大28 MB）をプログラムの隣に置くだけです。 確かに、関数を呼び出すときは、「bin \ win32」の場所を直接示すSetCurrentDirectory（）を使用する必要があります。 私は私のサプリメントでこれを行います。



次の関数が含まれます：ode23（）、ode45（）、ode113（）、ode15s（）、ode23s（）。





MatlabCppMathLibraryアドオンは 、c＃コードからこのライブラリを操作する方法を示しています。



参照：

1. 常微分方程式 。

2. MATLAB C ++数学ライブラリ。 ユーザーガイド。 バージョン2.1 （pdf）。

3. MATLAB C ++数学ライブラリ。 参照。 バージョン2 （pdf）。

4. MatlabCppMathLibraryアドオンのソース。



4. Octave C ++数学ライブラリ（Win32）



Matlab C ++ Math Libraryとほぼ同じですが、独自のゴキブリがあります。 残念ながら、私はこのライブラリでの作業を部分的にしか克服していません。 OctaveCppMathLibraryアドオンは 、c＃コードからこのライブラリを操作する方法を示しています。



参照：

1. 常微分方程式 。

2. OctaveCppMathLibraryアドオンのソース。



5. DotNumerics



次の関数が含まれます：AdamsMoulton（）、ExplicitRK45（）、ImplicitRK5（）、GearsBDF（）。 このライブラリは、Fortranから.Netに移植されています。 私は彼女が一番好きだった。 それは十分に速く動作します。



非剛性システムのソルバー：





スティッフシステムのソルバー：





さまざまな関数呼び出し形式には多くのオーバーロードがあります。 DotNumericsアドオンは 、このライブラリを操作する方法を示します。



参照：

1. DotNumerics 。

2. DotNumericsアドオンのソース。



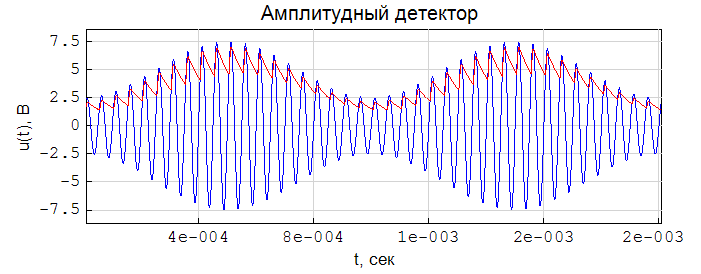
GearsBDF（）関数を使用してODEを解くとき、SMath Studioで振幅検出器モデルはどのように見えますか：



SMathスタジオ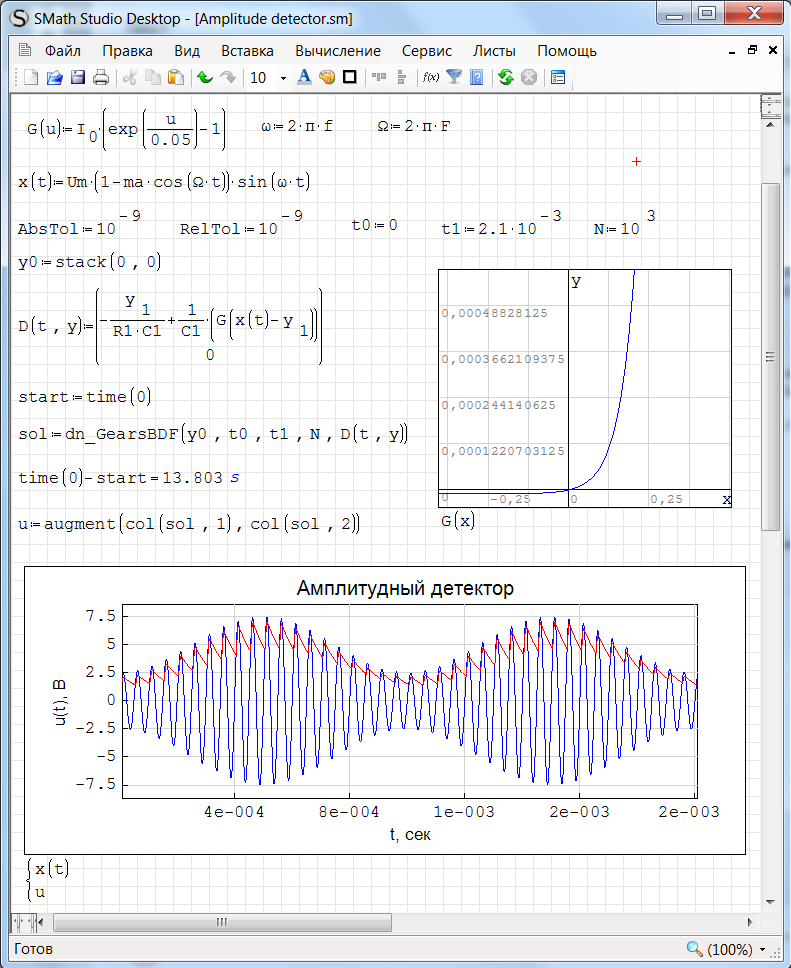






更新（2014年7月12日）。



6.ブースト:: odeint



次のアルゴリズムが含まれています。





まだ試していません。使用例を示すことはできません。



参照：

1. Boost.Numeric.Odeint 。

2. ステッパーの概要 。



7. SADEL（代数および微分方程式ソルバーライブラリのセット）



まだ試していません。使用例を示すことはできません。



参照：

1. SADELライブラリについて 。

2. 常微分方程式の硬いシステムの最新ソルバーとSADELライブラリのCソルバーの比較 。



8.ソルバーリモノバA. G.



まだ試していません。使用例を示すことはできません。



参照：

1. 論文。 複雑な係数を備えた2段式Rosenbrockスキームの開発と、周期的ナノ構造の形成のモデリング問題への応用、2010年 。


More articles:


All Articles