はじめに
友よ、今度は異常値(信号とは無関係)ノイズが存在する場合の線形回帰問題を考えてみましょう。 この問題は、音響処理[2]を含む画像処理(たとえば、カラーセグメンテーション[1])でしばしば発生します。 ランダム変数の座標を大まかに離散化でき、問題の次元が低い場合(2-3)、ロバスト回帰の標準的な方法に加えて、高速ハフ変換(BPH)[3]を使用できます。 この最後の方法を、精度と安定性の観点から「古典的な」方法と比較してみましょう。
線形回帰にBPHを使用する
平面上の線形回帰のタスクは、ペア(x、y)のセットとして定義された2つの変数間の線形関係を復元することです。 特定のレベルの座標の離散化を考えると、このセットをシングルビットまたは整数の画像に表示できます(最初のケースでは、ソースデータとその数にほぼそのような座標を持つポイントがあることにのみ注意してください)。 実際、ソースデータの2次元ヒストグラムについて話しています。 したがって、非公式には、表示されるポイントの分布を最もよく説明する画像上の線の検索にタスクを減らすことができ、そのような場合、画像処理にハフ変換が使用されます。
ハフ変換はラドン変換の離散アナログであり、画像の各ラインをそれに沿ったピクセルの輝度の合計に関連付けます(つまり、離散ラインに沿ったすべての種類の合計を同時に計算します)。 シフトとスロープによって直線を合理的に離散化することにより、平行な個別の線が平面を密に詰め込み、画像の一方の端のある点から出現する直線が反対の端の傾斜に沿って整数のピクセル数だけ発散するようにすることができます。 次に、正方形のn 2に約4 * n 2のこのような離散線が存在します。 この離散化のために、O(n 2 * log n)の漸近的な振る舞いでハフ変換を迅速に計算するためのアルゴリズムがあります。 このアルゴリズムは、高速フーリエ変換アルゴリズムによく似ており、並列化が良好で、加算以外の操作は不要です。 [3]では、これについてもう少し読むことができ、さらに、ガウスフィルターによって平滑化された画像からのハフ変換が線形回帰問題で一般に使用できる理由を説明します。 ここでは、この方法の安定性を示します。
試験データ
ここで、入力データにどのような分布が予想されるかを自問します。 音響的位置の問題では、船の軌道の直線セグメントに沿って点が均一に分布しており、通常の加算座標ノイズによって歪んでいると仮定できます。 色クラスタの分析の場合、セグメントに沿った分布は不明であり、しばしば非常に奇妙です。 簡単にするために、偏心度の高い2次元のガウス分布のみを考えます。 直接方向に沿った十分に大きな分散と、横方向の小さな分散により、構築された分布の特性は「ノイズの多いセグメント」とあまり変わりません。
テスト分布を生成するアルゴリズムは、次の3つのステップで説明できます。
- 「中心」と勾配はランダムに選択されます(線分がシミュレートされます)。
- 指定された分布(および選択された中心)で指定された数のポイントが生成されます。
- 均一な外れ値ノイズが追加されます。
直線に沿った正規分布の標準偏差は、モデル化されたセグメントの長さの4分の1(この選択では、ポイントの約95%が内部に収まります)であり、セグメントの長さは正方形の画像の線形サイズの半分(512ピクセル)であるとされました。 分散比は10.0で、分布点の数と外れ値ノイズの割合は変化しました。 この種の分布の例を図1に示します。
異なるアルゴリズムを比較するには、それぞれの場合にセグメントがどれだけうまく検出されたかを評価できる必要があります。 微妙な点は、問題のアルゴリズムがセグメントではなく直線を探していることです。 したがって、「理想的な」セグメント(A、B)を取得し、その端から実験的に見つかった直線までの最大2つの距離を見つけます。 Q(L、AB)が実験ラインLのパラメーターのエラーである場合、この定義は次のように記述できます:Q(L、AB)= max(r(L、A)、r(L、B))。
 |
FHLメソッドの誤差の平滑化ウィンドウのサイズへの依存
前述のように、BPHを使用した回帰は平滑化を意味します。 明らかに、平滑化ウィンドウのサイズはアルゴリズムの品質に大きな影響を与えるはずです。 直線を見つけることの誤差がウィンドウのサイズに依存することを調査します。 特定のセットのサイズごとに、一連の100個の画像が生成され、それぞれの直線が計算され、エラーが記録されました。 得られた結果を図2に示します。横軸は、座標ノイズs Lの標準(「横」)成分の標準偏差に対する平滑化パラメーターs Hの比率を定義します。 図の点は平均誤差を示し、標準偏差はそれらから上下にプロットされます。 s Hが s Lに近い場合に結果が最良であることがわかります。 ウィンドウサイズがセグメントの「厚さ」とあまり変わらない場合。
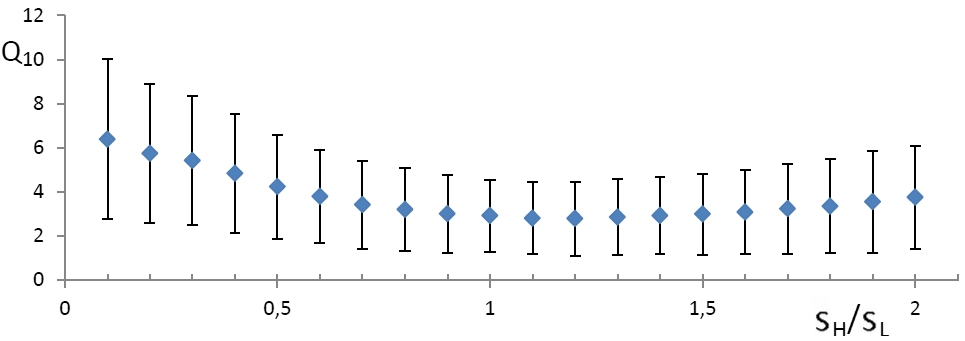 |
MNCおよびその堅牢な変更との比較
(このケースでは)正しくない線形回帰法は、当然ながら、最小二乗法(最小二乗法)であり、直交回帰では主成分法(PCA)と一致します。 かつて、外れ値ノイズの場合、「重みの反復再計算によるOLS」までドープされ、すべての教科書には、フーバー重み関数と双二次重み関数を持つバリアントが含まれていました[4]。
BPH法と単純な最小二乗法、および両方の重み関数で重みを再計算する最小二乗法と比較してください。 理論家が推奨するように、関数のパラメーターを使用します。フーバーではk H = 1.345、双二次関数ではk B = 4.685です。
図3は、4つの方法のそれぞれの平均誤差が放射ノイズ密度μにどのように依存するかを示しています-放射ノイズ点の数と画像内の全ピクセル数の比(放射ノイズ密度は横軸に沿ってプロットされ、方法の平均誤差は縦軸に表示されます)。 各測定は、生成された100種類の画像で実行されました。 図から、FHPの使用に基づく方法は、放出ノイズの追加に対して最も耐性があることが判明しましたが、放出点の数が少ないと、他の方法よりも精度が劣ります。 さらに、この方法はより安定していることがわかります。つまり、致命的なエラーを起こす可能性が低くなります(エラーの標準偏差の4分の1は、図の各ポイントから上下に延期されます)。
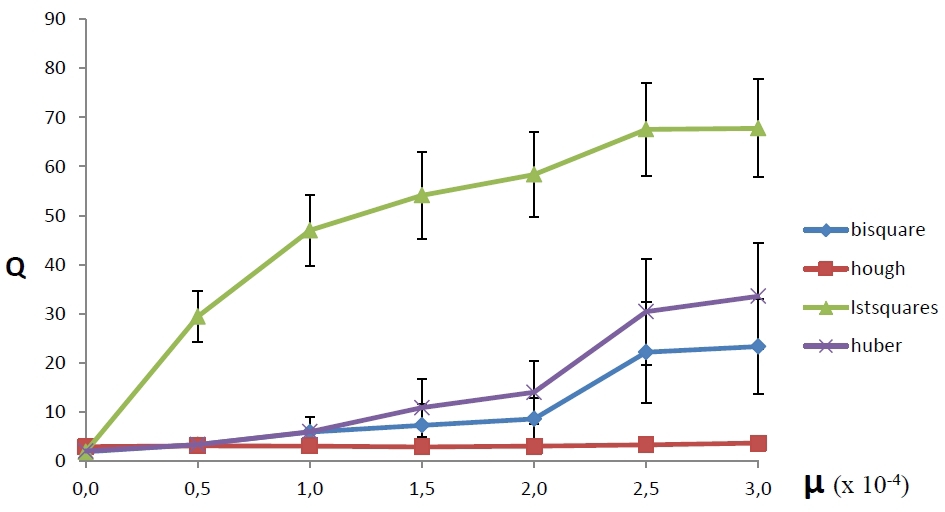 |
中央値法との比較
驚くべきことに、彼らは大学で本当に良いロバスト回帰法について語ることはめったにありません。 しかし、親愛なる読者は、魔法のTheil-Senメソッド[5]を知っているため、堅牢なOLSとの比較に限定するのは不名誉なことです。 古典的なTheil-Senアルゴリズムでは、線の勾配は、すべてのサンプルポイントのペアを通る線の勾配の中央値として計算されます。 さらに、修正版が使用されます。各分布点について、これと他の分布点を通過するすべての線の勾配の中央値が最初に選択され、その後、中央値(「中央値の中央値」)が取得値から選択されます。 どちらの場合も、ラインシフトパラメーターを決定するために、値{y i -mx i }の中央値が取られます。ここで、mは、説明されている方法で見つかったラインの角度係数です。
図4は、これらの方法との比較を示しています。 各シリーズの一環として、100回の実験がまだ行われ、名称も変更されませんでした。 考えられる放射ノイズ密度の範囲では、BPH法の平均誤差は最小であり、増加しませんが、Theil-Sen法では比例誤差が増加します。 また、FHLメソッドの誤差の広がりが最も小さいこともわかります。
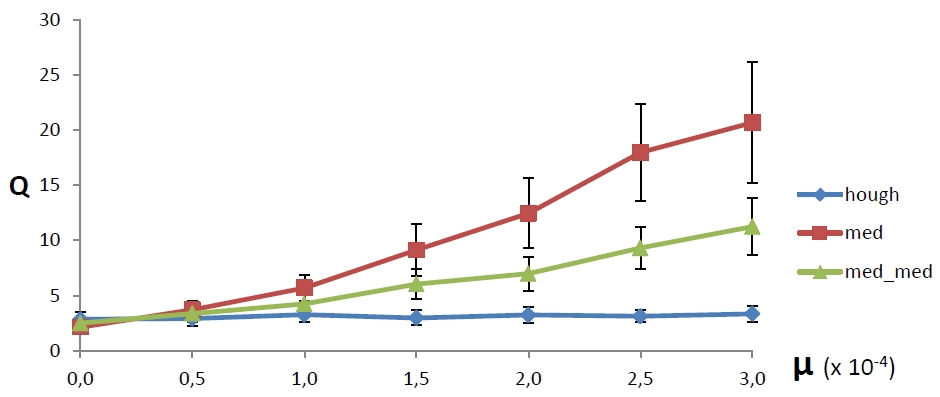 |
構造化ノイズが存在する場合の方法の比較
特に興味深いのは、外れ値ノイズが独自の空間構造を持つ場合です。 例として、既に検討されているタイプのノイズに、円形の2次元正規分布を持つ信号と相関のないノイズ成分を追加します。 3種類すべてのノイズの組み合わせの例を図5に示します。直線は完璧な答えを示しています。
 |
ここで、異常値と加法性ノイズの固定パラメーターを使用して、「ラウンド」構造化ノイズの密度に対するエラーの依存性を見てみましょう。 前と同様に、各濃度値に対して100個の画像が生成されました。 結果を図6に示します。メソッドが3つのグループに分けられていることは注目に値します。驚くべきことに、古典的な堅牢なメソッドはOLSとほとんど違いがありません。 すべてのMNCメソッドの「ブレークダウン」はほぼ即座に発生し、中央値のメソッドははるかに大きなデータ汚染で安定して動作しますが、遅かれ早かれ動作しなくなりますが、BPHメソッドは急激なブレークダウンを示しません。
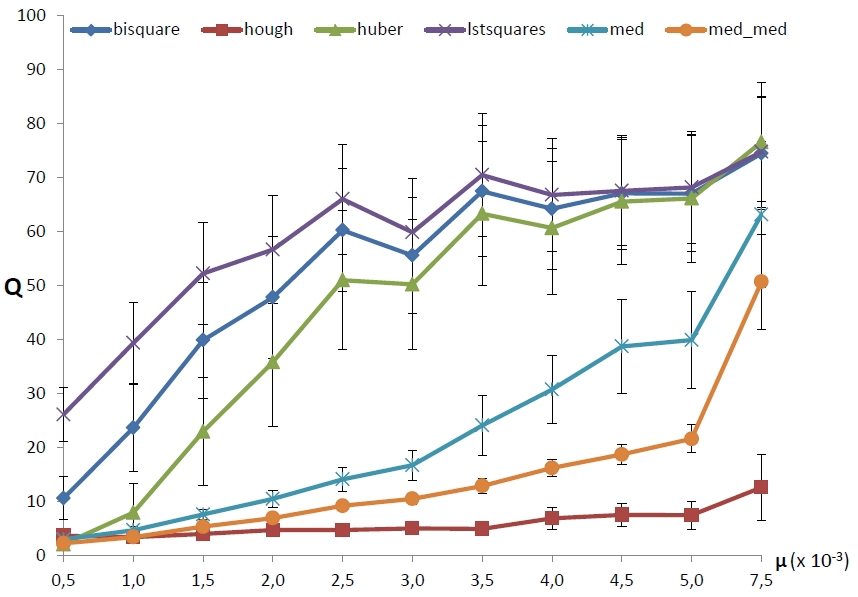 |
議論
ガウス平滑化とハフ変換の組み合わせを使用して線形回帰問題を解くことは、同時に存在する加法座標と外れ値ノイズに耐性があります。 他の一般的な堅牢な方法との比較により、提案されたアルゴリズムは、放射ノイズ密度が十分に高い場合により安定していることが示されました。 同時に、この方法は小さな場合にのみ適用できることに注意する必要があります(BPHアルゴリズムは任意の次元に一般化できますが、タスクを3次元以上の画像の形式でエンコードするために必要なメモリ量は恐ろしいです)。 さらに、2次元の場合でも、ポイントが少ないとBPHの使用は不利になり、必要な相対座標精度は高くなります。 これは、他の方法の場合、計算の複雑さはポイントの数に依存し、BPHでは離散空間の数に依存するという事実によるものです。 ただし、少数のポイントでは、「ブルートフォース」によってハフ変換を計算することができます。 最初に画像を滑らかにしたいので、そのようには見えませんが、イスラエルのMoiseyevich Gelfandでさえ、特定の意味でのガウス平滑化がラドン変換と交換することを知っていました。 このトリックを使用すると、少数の点の近似におけるメソッドの漸近性をO(n 2 )に改善できますが、nはまだ画像の線形サイズであるため、ほぼ間違いなく悪すぎます。 しかし、多数のポイントがあるため、BPHメソッドは、雄牛(羊)のような他のすべてのメソッドをカバーしています。 そのようなこと。文学
[1] DPニコラエフ、PPニコラエフ線形カラーセグメンテーションとその実装、コンピュータービジョンと画像理解。 2004、V.94(画像のインデックス作成と検索のための色に関する特別号)、pp。 115-139
[2] L.ノーレ。 ターゲット追跡のための計算知能の応用。 Procで モデリングとシミュレーションに関する第21回欧州会議、2007、pp。 289-293。
[3] DPニコラエフ、SMカルペンコ、IPニコラエフ、PPニコラエフ。 ハフ変換:コンピュータービジョン分野の過小評価ツール。 Procで 第22回モデリングとシミュレーションに関する欧州会議、2008年、pp。 238-243。
[4] PJ Rousseeuw、AMリロイ。 ロバストな回帰と外れ値の検出。 確率と統計のWileyシリーズ、2003年。
[5]ウィルコックス、R。ランド。 Theil – Sen Estimator、ロバスト推定と仮説検定入門、アカデミックプレス、2005年、pp。 423-427。