アルゴリズム自体は、2つのステートメントと2つの定理に基づいています。その証明は、かなりの量があるため、ここでは示しません。
最初に、実際に探しているものを決定します。
有限集合を与えよう
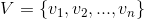 と家族
と家族 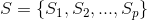 そのサブセット
そのサブセット 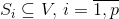 。
。
サブファミリーを見つける
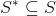 (存在する場合)そのような
(存在する場合)そのような 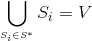 そして、サブファミリーS *(集合Vのカバー)のパワーは、可能な限り最小です。
そして、サブファミリーS *(集合Vのカバー)のパワーは、可能な限り最小です。
次のステートメントは、最小および最小カバレッジの概念を定義しています。
ステートメント1
サブファミリーへ
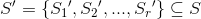 多数のカバーでした
多数のカバーでした 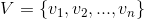 、それは条件のために必要かつ十分です
、それは条件のために必要かつ十分です
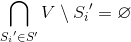
カバリングSは、「カバリングSがない場合、最小と呼ばれます」
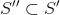 。
。
カバリングS *は、最小限のカバリングSの場合、最小と呼ばれます。
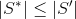
ステートメント2
カバレッジ
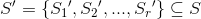 いずれかの場合にのみ最小
いずれかの場合にのみ最小 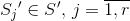 、条件
、条件
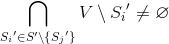
そして、最も基本的な。
有限集合を与えよう
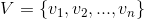 と家族
と家族 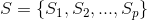 そのサブセット
そのサブセット 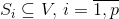 。
。
完全にロードされたグラフを作成します
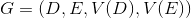 セットで
セットで 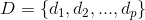 グラフの頂点は、ファミリに一意に関連付けられています
グラフの頂点は、ファミリに一意に関連付けられています 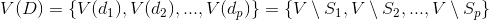 サブセット
サブセット  、
、
そして各rib骨に
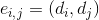 -サブセット
-サブセット 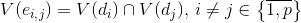 。
。
示す
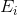 上部に入射するすべてのエッジのセット
上部に入射するすべてのエッジのセット 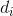 、そして
、そして 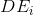 -セットのエッジに入射するすべての頂点のセット
-セットのエッジに入射するすべての頂点のセット 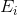 。
。
定理1
最小電力サブセット
 任意の頂点に付随するエッジ
任意の頂点に付随するエッジ 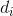 列Gの条件下で
列Gの条件下で
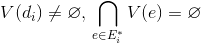
最小カバレッジを決定します
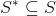 セットに一意に対応
セットに一意に対応 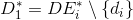 頂点
頂点 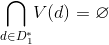 、または多くの
、または多くの 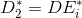 頂点
頂点 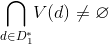 。
。
定理2
最小電力サブセット
 任意の頂点に付随するエッジ
任意の頂点に付随するエッジ 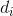 rib骨
rib骨 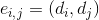 列Gの条件下で
列Gの条件下で
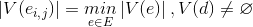 すべてのために
すべてのために 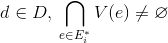
最小のカバレッジを決定します
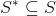 セットに一意に対応
セットに一意に対応 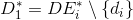 頂点
頂点 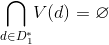 、または多くの
、または多くの 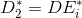 頂点
頂点 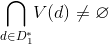 。
。
定理に基づいて、最小のカバレッジを見つけるための次のアルゴリズムが提案されています。
1.多くの
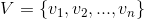 と家族
と家族 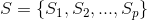 そのサブセット
そのサブセット 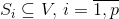 マッチ家族
マッチ家族 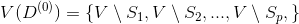 サブセット
サブセット 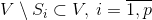 。 一部の場合
。 一部の場合 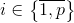 なります
なります 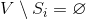 、それから些細なカバーがあります
、それから些細なカバーがあります 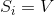 。 アルゴリズムの終わり。
。 アルゴリズムの終わり。
それ以外の場合は、手順2に進みます。
2.完全にロードされたグラフを作成する
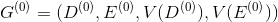 どこで
どこで 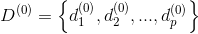 。
。
トップ
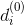 たくさんロードする
たくさんロードする 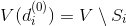
リブ
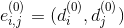 たくさんロードする
たくさんロードする 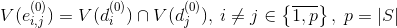 。
。
3.カバレッジの存在を確認します:任意の頂点について
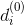 サブセットを定義する
サブセットを定義する
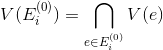 、
、
どこで
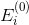 -上部に多くのエッジが入射
-上部に多くのエッジが入射 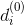 グラフで
グラフで 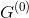 。
。
もし
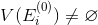 その場合、カバレッジは存在しません。 アルゴリズムの終わり。
その場合、カバレッジは存在しません。 アルゴリズムの終わり。
もし
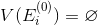 カバレッジが存在します。 最小のカバレッジを見つける手順に進みます(セクション4)。
カバレッジが存在します。 最小のカバレッジを見つける手順に進みます(セクション4)。
4. t:= 0と入力します。
5.完全にロードされた列
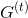 リブを見つける
リブを見つける 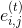 条件が満たされているもの
条件が満たされているもの 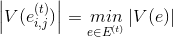 。
。
もし
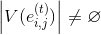 次に、手順6に進みます
次に、手順6に進みます
そうでない場合、最小カバレッジを定義するD頂点のセットを構築する手順
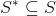 (パラグラフ7)。
(パラグラフ7)。
6.完全にロードされたグラフを作成する
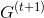 信じる
信じる  、
、 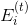 -上部に多くのエッジが入射
-上部に多くのエッジが入射 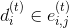 グラフで
グラフで  。
。
置く
 すべてのために
すべてのために  。
。
t:= t + 1と入力して、ステップ5に進みます。
7.最小カバレッジを定義する頂点のセットDの構築の開始
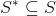 。
。
置く
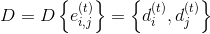 。
。
8. t = 0の場合は手順11に進み、そうでない場合はt:= t-1を入力します。
9.列
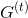 サブセットを定義する
サブセットを定義する 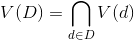
10.列にある場合
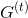 条件が満たされている
条件が満たされている 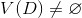 次に置く
次に置く 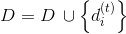 それ以外の場合-D:=D。 ステップ8に進みます。
それ以外の場合-D:=D。 ステップ8に進みます。
11.ファミリー
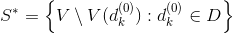 サブセット
サブセット 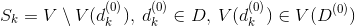 セットの最小カバレッジを定義します
セットの最小カバレッジを定義します 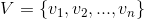 。
。
アルゴリズムの終わり。
アルゴリズムの複雑さを評価してみましょう。
アルゴリズムの本質は、いわば(複雑性評価の観点から)、「完全なロードグラフを構築します」というフレーズに含まれています。
n個のアクションを実行して、グラフのn個の頂点での負荷を計算し、(n-1)n / 2個の計算(グラフ全体の端の数による)グラフの端の負荷を実行する必要があります。 そして、これらすべてが、最悪のケースを考慮すると、サブセットが交差しない場合、n-2回実行されます。 したがって、概算はO(n)= n 3 + n 2です。
そして結論として。 アルゴリズムへの私の関与が疑わしいため、投稿が招待に値するかどうかはわかりません。 しかし、この出版物は価値があるように思えます。 モデレーターが整理することを望みます。
ギリシャ人はそこで何と言いましたか? -Fais se que dois adviegne que peut(あなたがしなければならないことをして、何が起こるか)。
(または彼らはローマ人でしたか?)