私は音楽が好きでプログラマーであることがたまたまありました。かつて私はこれを組み合わせたかったのです。
それが何をもたらしたのかをお伝えします。
この記事では、どの楽器でメロディーを演奏するかを決定できるアルゴリズムを作成しようとした方法について説明します。
さあ行こう
生データ:
- 10台の楽器で5分間で550レコード-楽器ごとに55レコード。
- 楽器:ピアノ、チェロ、ドンブラ、フルート、パイプ、ギター、アコーディオン、クラリネット、ヴィオラ、バイオリン。
- 音楽信号の9つの兆候。
最後に何が欲しいですか?
その結果、音楽信号を分類し、分類アルゴリズムの基礎を形成するのに役立つ記号の値を取得したいと思います。
どうしますか
戦略は次のとおりです。
- 入力準備
- クラスター分析
- 入力次元の削減
- 分類ツリー分析
実際、これについてはさらに説明します。
入力準備
この段階では、さまざまな方法(フーリエ解析など)を使用して、9つの特性の値を取得します。
クラスター分析
階層分類法を使用します。 この方法によるクラスタリングの結果を次の図に示します(クラスターは赤丸で強調表示されています)。
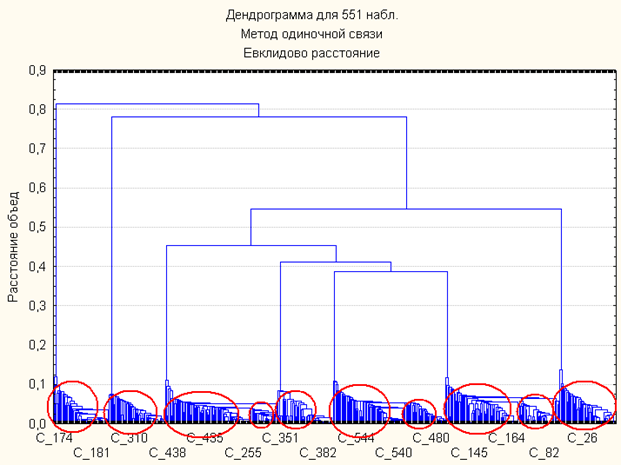
この場合、先験的にわかっている10個のクラスターを観察できるため、利用可能な入力データのセットに従って分類する可能性がまだあります。
入力次元の削減
私たちが自由に使える入力データのセットはかなり大きな次元を持っているので、それを扱うのはあまり便利ではありません。 入力データの次元を減らす、つまり、データ削減の問題を解決しようとしましょう。
これを行うには、まず粗いツールとして因子分析を使用してから、多次元尺度法を因子分析の結果に適用します。
因子分析を実施します。 いくつの要素が割り当てられるかわからないため、9つの要素に費やします。 固有値は次の表に示されています。
固有値ハイライト:主なコンポーネント
すすり泣き。 キャラクター 総分散の%累積。 累積値 %
1 3.640494 40.44993 3.640494 40.4499
2 1.875795 20.84217 5.516289 61.2921
3 1.028626 11.42918 6.544915 72.7213
4 0.869353 9.65948 7.414268 82.3808
5 0.636831 7.07590 8.051100 89.4567
6 0.410692 4.56325 8.461792 94.0199
7 0.261768 2.90854 8.723560 96.9284
8 0.204545 2.27272 8.928105 99.22012
9 0.071895 0.79883 9.000000 100.0000
この表からわかるように、説明された分散の合計シェアは80%を超えません。ここから、データが非線形である、つまりデータが非線形モデルで近似されていると結論付けることができます。 要因の数は、画面のスケジュールによって判断できます。
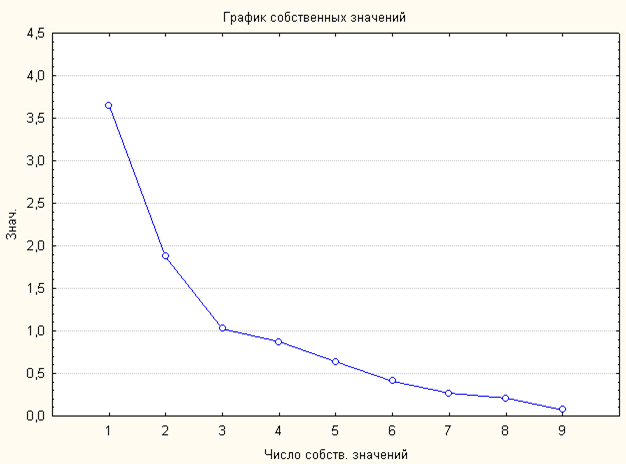
スクリープロットによれば、3つの要因を区別できることがわかります。
多次元尺度法を使用した分析では、データ削減の状況は改善されませんでした。 多次元スケーリングを実行しても結果が得られなかったという事実は、シェパード図によって証明されています。シェパード図は、分析を成功させるためには直線でなければなりません。
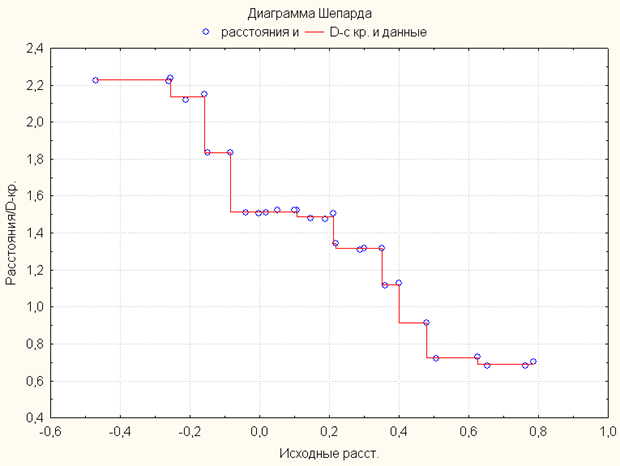
分類ツリー分析
初期データの10個のクラスターの存在についてアプリオリを知っているという事実、およびそれらの存在の証拠がある(つまり、利用可能な一連の特性に応じて分類される可能性がある)という事実を考慮して:入力データの調査-分類ツリー-非常に「薄い」ツールを使用することが決定されました。 また、分類問題の最も正確な方法として、CARTメソッドに従って1次元分岐を適用することも決定されました。
このアルゴリズムは、次の分類ツリーを構築しました。
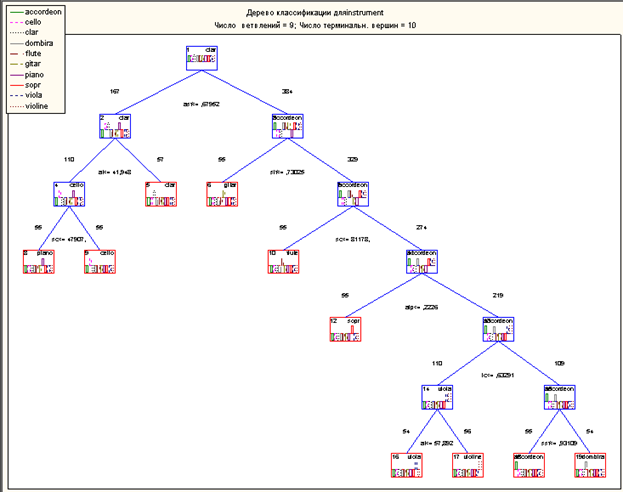
得られた結果を説明しましょう。 ご覧のとおり、分類ツリーは正しく構築されています。末端の頂点に繰り返しがないため、入力データに提示されたオーディオ信号の特性の値に基づいてクラスに明確に分割されました。
おわりに
すべての実験は、仲間のミュージシャンとStatistica数学パッケージの助けを借りて行われました。
その結果、オーディオ信号の兆候の値が得られました。そのおかげで、どの楽器でメロディが演奏されたかを認識できます。
これまでのアルゴリズムは、同じ楽器で演奏されるメロディーで機能しますが、複数楽器のメロディーも計画されています。