
ここでそのようなプログラムの根底にあるアルゴリズムの何らかの考えを見つけることができます 。
開発されたプログラムでは、問題の解決策を入力するための2つのインターフェイス、「難しい」と「簡単」が利用できます。 以下は、それぞれの詳細な説明です。
難しいインターフェイス
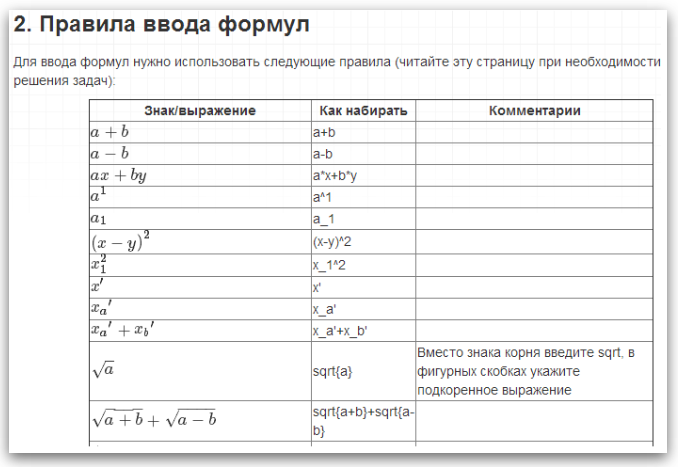
ソリューションのステップとして、学生はLaTeXのような構文の式をプログラムに入力します。 数式を入力するための構文はやや単純化されています。 たとえば、行列の入力は次のとおりです。
[1,2;3,4;5,6]
数式の入力中、その視覚的表現は入力ステップの形式で動的に形成されます。 生徒が数式を入力した後、「ステップの確認」ボタンをクリックします。 ステップが正しい場合、テストされた数式は「Solution」という見出しのある領域に移動します。 それ以外の場合、ステップ入力フォームの一部の要素は赤色になります。
生徒はいつでも、対応する名前のボタンをクリックして、数式を入力するためのルールを確認できます。 数式を入力するためのルールは、可能な限り簡潔に、説明付きの例の形式で記述されました。
読者は、なぜプログラムで視覚的な数式エディターを作成しなかったのかと尋ねるかもしれません。 事実は、この場合、学生は検証のためにあまりにも多くの式を送信し、その正確性を確立するのは難しいだろうということです。 残念ながら、学生の推論のコースをプログラムで評価できるようにするには、決定手順の入力方法に制限を課す必要があります。 プログラムのコードベースが発展するにつれて、制限の厳しさを軽減できます。
プログラムの現在のバージョンでは、次の制限が適用されます(これらはプログラムインターフェイスのヘルプからの断片です)。


次の図は、生徒がタスク設定で指定されていない指定を使用したため、生徒のステップが正しくないと認識されたことを示しています。

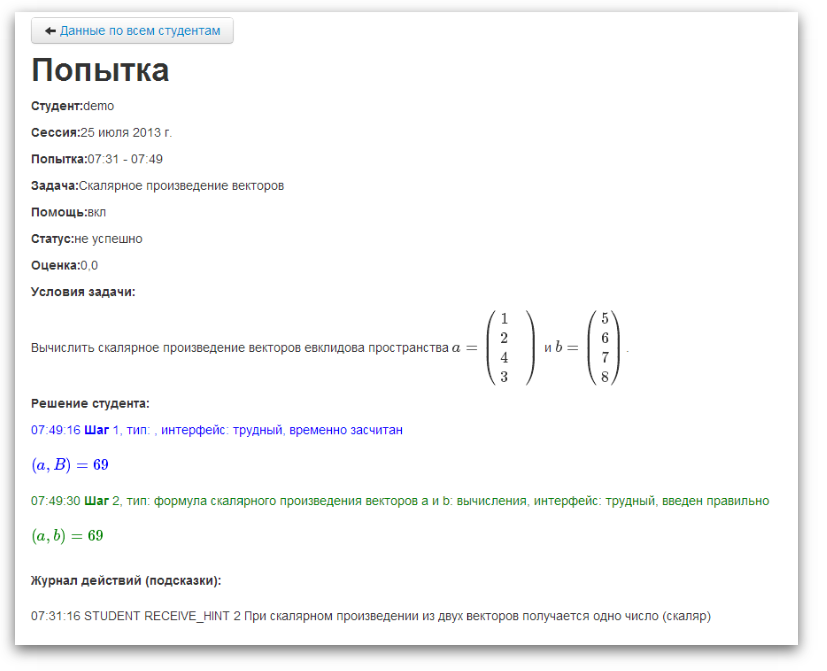
学生はコース作成者が意図していない意思決定ステップをいつでも入力できるため、苦情処理メカニズムはプログラムに実装されました。その本質は次のとおりです。 学生によると、プログラムが間違っていて、自分のステップが正しいとカウントされない場合、[苦情]ボタンをクリックできます。 その後、ステップは正しいものとしてカウントされます。 その後、ステップのステータスは教師が変更できます。 問題解決に関するレポートは、アプリケーションの管理パネルで教師が利用できます。そこでは、そのような手順が強調表示され、特別なステータスが与えられます。
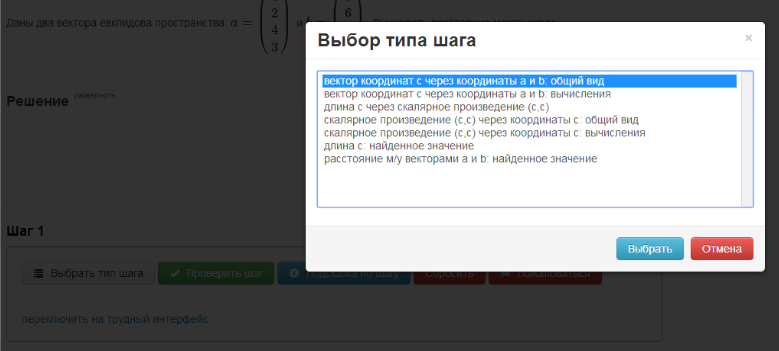
簡単なインターフェース
このインターフェイスを使用する場合、学生は最初に目的のステップのタイプを選択します(ステップのタイプはコース作成者によってプログラムに入力されます)。
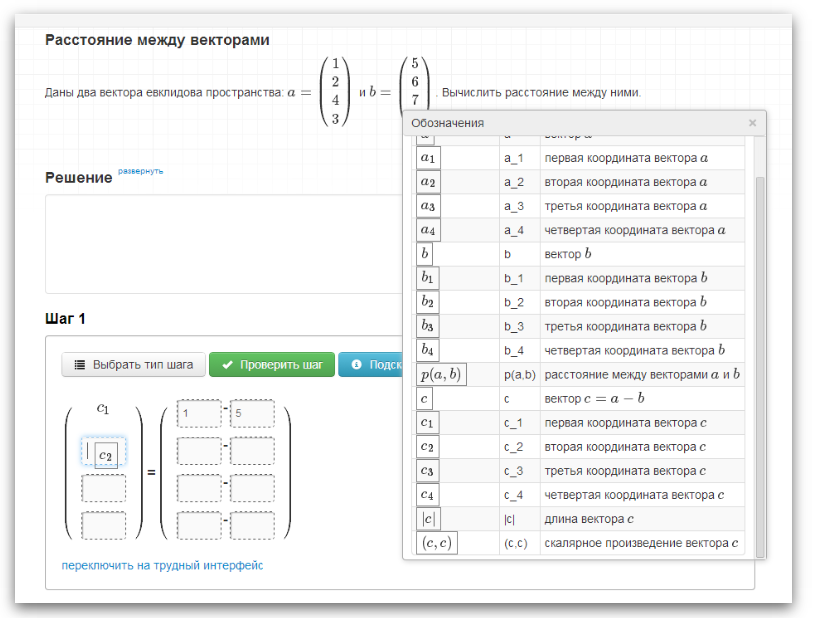
その後、式テンプレートがステップ入力フォームにロードされます。

次に、生徒はテンプレートの空白を埋め、手で数字を入力し、「記号」ウィンドウから記号をドラッグします。
両方のインターフェースをテストする
使いやすさのテスト(あるいは、力とタイミングが許す限り、その見た目は)2回実行されたと言えます。 初めて、ある州立大学の心理学部のフルタイムの学生数名と夕方の学生数名が捕まった。 学生は、プログラムインターフェイスの習得に役立つチュートリアルを実行するように求められました。 チュートリアルには、理論的な資料と2つのタスクが含まれていました。 学生のフィードバックが収集され、さらに、プログラムでの学生の作品のビデオが分析されました。 ビデオには、生徒の画面で起こっていることだけでなく、顔も記録されています。
2回目は、フルタイムの学生グループ全体がカリキュラムに参加し、カリキュラムのタスクを正常に完了した場合に試験の自動評価を受ける機会が提供されました。 この段階で、生徒の作品のビデオ録画とその解決策が分析されました。
最初の「ユーザビリティテスト」後の学生のフィードバック
10人の学生がインタビューされました。 以下は受け取ったフィードバックです。 レビューから、最初に、「私はすべてが好きで、コメントはありません」などの情報量の少ないタイプを除外し、次にプログラムでその後修正されたものを除外しました。 調査参加者から取得したパフォーマンスデータ。
1.性別:妻、学業成績:cf
私が気に入ったのは、知識のない人の課題を解決する機会があることです。 ヒントは本当に役立ちます。 気に入らなかった点:決定するのに時間がかかりすぎるため、ボタンを何度もクリックする必要があります。 たとえば、手動で二次方程式を解く方が、このプログラムを使用するよりも高速です。
2.性別:妻、グレード:高
このプログラムは、ネットワーク上で必要なものがすべて揃っているという点で便利です。 インストールして待つ必要はありません。 速く動作します。 受け入れられた表記法を入力する場合にのみ、二次方程式を使用する必要がありました。 軽量、手頃な価格、快適
3.性別:妻、学業成績:高
私は好きだった:すべての必要な機能があり、ヒントがあります。 グリッチなしで動作します。 気に入らなかった。ステップに入るのに時間がかかりすぎる。
4.性別:夫、パフォーマンス:cf。
「ステップの追加、ヒントの取得」メニューとヒントが画面上のカーソルとともに移動して、常に表示されるようにすると非常に便利です。 不便なのは、エラーが発生すると、コンピューターが式全体を赤で強調表示し、カウントできない場所ではなく、エラーを探す必要があるためです。
5.性別:女性、パフォーマンス:高
係数が1の場合、不必要な作業を行う可能性があり、それらを分割または乗算する必要があるのが便利です。 いいね:手がかりがあります。
6.性別:夫、パフォーマンス:cf。
数学記号と関数記号の通常の入力が好きでした。 <...>
7.性別:女性、パフォーマンス:高
トレーニングマニュアルを使用して、すばやく簡単に文字を入力できることが気に入りました。 ユーザーフレンドリーなインターフェース、すべてが十分に明確です。 Macbookのレイアウトに慣れて操作すると、すぐにわかります。 <...>答えが間違っている場合-エラーに関するコメントがありません-そのような関数があればより便利です。 シートに頼るのがより一般的であるため、今プログラムを使用するように申し出られたら、まずシートを決めてから、結果をウィンドウに書き込むと思います。 学校にそのようなプログラムがあれば、勉強しやすいかもしれません。
フィードバックが収集されるまでに、ステップタイプ選択ウィンドウには、教師が推奨するソリューションからのステップのタイプだけでなく、タイプデータベースからランダムに選択された2-3が表示されることに注意してください。 このようにして、生徒の問題を解決するための計画を「ぼかす」ことができると想定されたので、彼自身が各タイプのステップについて考えるようになりました。 テストの結果、このような選択があると、最も上級の学生でも混乱することがわかりました。 多くの学生は、各タイプのステップの名前を長い間読んで、それが何であるかを理解しようとしており、彼らの選択を完全に確信していませんでした。 したがって、プログラムの次のバージョンでは「余分な」タイプはありませんでした。
2回目の「ユーザビリティテスト」の結果
23人の学生がテストに参加しました。 成績の高い学生と、学業成績が平均または低い学生の両方が参加しました(成績評価は宿題の成績に基づいて計算されました)。 ユーザビリティテストのデータは間接的に収集されたため(プログラムでの学生の作業の主な目標ではありませんでした)、収集されたデータに基づいて結論を引き出すことはできません。 しかし、あなたは仮説を立てることができます:)
学生は、プログラムインターフェイスでトレーニングを受け、次にさまざまな複雑さの1つまたは2つの問題を解決するように求められました。 多くの学生は、より高い成績を得るために、3つの問題すべてを解決しようとしました。 トレーニングプログラムで問題を完全に解決できなかった人たちは、教師にpsペーパーに解決策を渡しました。
プログラムのインターフェースを学習するのにかかる平均時間は、学業成績が高い学生では23分、学業成績が平均または低い学生では32分かかりました。 学業成績の高い2人の学生がプログラムインターフェイスのヘルプをスキャンしましたが、演習は行いませんでした(その後、学生の1人は問題を解決しませんでした)。 すべての学生が希望どおりにインターフェイスのチュートリアルを行ったわけではありません。 多くの学生は、インターフェイスを習得するのに役立つ問題を解決する前に、チュートリアルのすべてのページをめくり、次に何が待っているのかを理解しようとしました。 チュートリアルのページを前後にジャンプしました。 チュートリアルページで1つまたは2つのステップを入力して次のセクションに進むように求められたにもかかわらず、問題を最後まで解決し、100%のスコアを獲得するのに苦労した愛好家がいました。
インターフェイスを習得するのに役立つタスクの文言は次のとおりです。


一部の学生は、「簡単」または「難しい」インターフェースでのトレーニングをスキップし、解決しようとする資料のみを調べました。 他の学生は特定の瞬間を逃し、すでに問題を解決する過程でプログラムにデータを入力することの複雑さを完全に理解しました。 ある生徒は、数式を入力するための構文を非常に興味深く研究しました。 この生徒は、複雑な数式に1つまたは別の記号を追加し、ステップの入力をデバッグするかのように、視覚表現がどのように変化するかを観察しました。
以下は、中複雑度および高複雑度の問題を解決した結果に関するデータです。 インジケータ「不正なステップの割合」の値は、トレーニングプログラムが不正とマークした学生の意思決定ステップの数と、学生の意思決定ステップの総数との比率として計算されます。 生徒が問題の解決方法を知っている場合、インジケーターの対応する値は、特定のプログラムインターフェイスのソリューションを入力する難しさと、導入された式の形式に関する現在の制限を特徴付けます。 表では、指定F、A、Iを使用して、生徒は高い、中程度、および低い学業成績でエンコードされています。
表1.タスク「ベクトル間の距離」のソリューションに関するデータ
| いや | 学業成績 | 解決済み、% | コスト。 t分 | 間違ったステップの割合 | トータルステップ |
| 1 | 私は | 1 | 29日 | 0.52 | 27 |
| 2 | 私は | 1 | 19 | 0.44 | 16 |
| 3 | A | 1 | 12 | 0.09 | 11 |
| 4 | A | 1 | 24 | 0.76 | 29日 |
| 5 | A | 1 | 29日 | 0.56 | 23 |
| 6 | A | 1 | 33 | 0.42 | 12 |
| 7 | A | 1 | 21 | 0.6 | 30 |
| 8 | F | 1 | 13 | 0.22 | 9 |
| 9 | F | 1 | 10 | 0.1 | 10 |
| 10 | F | 1 | 7 | 0 | 10 |
| 11 | F | 0 | 1 | 1 | 2 |
表2.「異なるベースのスカラー製品」という問題の解決策に関するデータ
| いや | 学業成績 | 解決済み、% | コスト。 t分 | 間違ったステップの割合 | トータルステップ |
| 1 | 私は | 0.9 | 33 | 0.46 | 28 |
| 2 | A | 1 | 35 | 0.62 | 29日 |
| 3 | A | 0.8 | 33 | 0.12 | 17 |
| 4 | A | 0.5 | 23 | 0.45 | 22 |
| 5 | A | 0.5 | 80 | 0.41 | 54 |
| 6 | A | 0.9 | 26 | 0.17 | 30 |
| 7 | F | 0.5 | 80 | 0.76 | 49 |
| 8 | F | 0.5 | 43 | 0.73 | 25 |
| 9 | F | 0.5 | 18 | 0.25 | 16 |
| 10 | F | 0.5 | 39 | 0.2 | 15 |
| 11 | F | 0.2 | 70 | 0.79 | 29日 |
| 12 | F | 1 | 78 | 0.61 | 18 |
| 13 | F | 0.7 | 63 | 0.8 | 25 |
| 14 | F | 1 | 32 | 0.32 | 34 |
| 15 | F | 1 | 22 | 0.17 | 23 |
苦情処理メカニズムは、最も難しい問題を解決した学生のみが使用しました。 4人の学生がプログラムについて不満を述べたが、苦情はすべての場合に実証されたわけではなかった。 プログラムのステップで誤って認識されたのは8人の学生の決定で満たされ、合計18のそのようなステップがありました。 これらのステップの分析は以下を示しました。
- 最も一般的な理由は、予期しない式でした(つまり、問題のすべての可能な解決策がプログラムに含まれていなかった)。
- システムが入力された数式を誤って認識する理由としてよくあるのは、表記をドラッグして簡単なインターフェイスに数式を入力する代わりに、生徒がキーボードから独立して文字を入力した場合です。 これは、簡単なインターフェイスの直感性に関する非常に有用な発言と考えることができます。 このような入力シナリオが想定されていたはずです。
「典型的な間違い」ページの存在にもかかわらず、学生はしばしばいくつかの式の代わりにフォームの1つの式を入力しました
または(c,c) = (1-3)^2 + (2-4)^2 = 8
そしてその後、彼らはボタン「チェックステップ」をクリックしました。(c,c) = (1-3)^2 + (2-4)^2, (c,c) = 8
また、このプログラムは、この決定または学生が予想したよりも低い決定を下したことが判明しました。 これは、トレーニングプログラムのデータベースで決定を行う際に、解の各ステップが2つの式に対応していると想定されていたためです。表記法による代数式と直接計算による式です。 例:
そして(a,b) = x_a*x_b+y_a*y_b
(a,b) = 1*2+3*4
学生は解を書くための予想される形式については教えられなかったので、代数的表現に対応する式をしばしば省略しました。 一方、ソリューションの進捗状況を測定するアルゴリズムには、まず代数表現が必要です。生徒の式がより複雑に計算されるほど、問題を解決する方法の不確実性が大きくなります(大まかに言うと、生徒が単にソリューションを導入した場合a = 6?)
多くの場合、生徒は最初に問題を紙で解決し、次にその解決策をカリキュラムに導入しました。
おわりに
むかしむかし、実験に生徒を提供した教師だけでなく、この投稿の著者も、人文科学がLaTeXのような構文で数式を導入できるとは信じていませんでした。 これが間違っていることが判明したとき、私たちは皆非常に驚きました( ミハイル・フィロネンコのおかげで、この方法で解決策を試してみませんか?)
当社が開発した現在のバージョンのトレーニングプログラムには改善の余地があります。 トレーニングプログラムが線形代数の3つの問題ではなく、さらに多くの問題をチェックできるようにするには、多くのプログラムコードを追加する必要があります。
まず、「簡略化された」構文を使用して導入された数式の翻訳モジュールを拡張する必要があります
- Mathjax(学生が入力した数式の視覚的表現を動的に形成するのに役立つライブラリ)の構文に;
- シンボリック計算のSymPyライブラリが理解する構文に、どの生徒の決定が検証されるかを助けます。
これらの構文はすべて似ていますが、独自のニュアンスがあります。
第二に、このようなシステムの重要な場所の1つは、意思決定検証モジュールです。 この方向で、学生の決定の進捗を測定するためのアルゴリズムが開発されています(このアルゴリズムとその代替の説明には、別の投稿が必要です)。
簡単にソフトウェアの実装について
- サーバー言語とフレームワーク-Python + Django、
- 数式検証ロジック-ヒューリスティックアルゴリズム+ SymPy(Python)、
- クライアント-JavaScript + jQuery + MathJax、
- カスタマークリアランス-Twitterブートストラップ。