イントロ
このトピックをチュートリアルとして公開します。 実際のところ、この資料には重要な新規性はありません。このトピックはハックされています。 この問題を解決するアプローチは興味深いと思います。
数学的分析のクラスの最初の年に、ある積分が思い浮かんだことを覚えています。 先生はボードに電話しましたが、ベルが鳴りました。 家に帰る途中で、バスで三次方程式を解く「スケルトン」が形になりました。 もちろん、一般的なスキームは最も合理的ではありません。 より効果的な三角関数のVieta式があります。 そこでは、根は方程式の形ですぐに記述されますが、一般に、計算量の観点からは、逆三角関数のべき級数がゆっくり収束するため、ニュートン数値法を使用することをお勧めします（これらは一部のライブラリでそのような関数の計算を構築するために使用されます）。 これが何が起こったのかです。
1.初期積分と3次方程式
不定積分を見つける必要がある
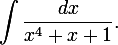
不確かな係数の方法を使用して、被積分関数の分母を次のように表します。
そこから、未知の係数の代数方程式の非線形システムを取得します。その解法には、不完全な立方方程式の正の根を見つける必要があります。
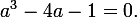
探索機能
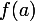単調性方程式の左側で、最大値を持つことがわかります
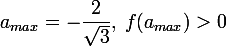
そして最小
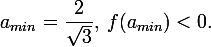
同時に
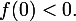
次に、関数の連続性から
元の方程式には3つの実根があり、2つの負と1つの正がセグメントに属している 
、 
。
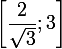彼を見つけます。
2.肯定的な解決策を探す
この方程式には有理根がないことに注意してください。
以下のアイデンティティから始めましょう。正義は、おそらく多くの人が学校で議論したものです。
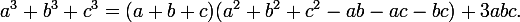
タイプに変換する
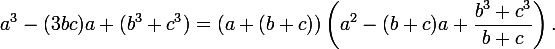
次に、三次方程式の解は、システムの解に還元されます
さらに
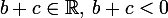（ルートの陽性の条件による）。
このシステムからシステムに移動しましょう
実際、二次方程式のVietaの定理は（1）に記述されています。
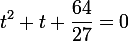
または
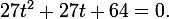
判別式はここでは否定的であり、決定を完了することができるように思われますが、現実は必要ありません
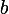そして 
、およびその金額の有効性。 複素数が役立ちます。
二次方程式の根を書く三角形式の形式は
、
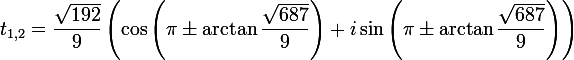どこで
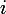-虚数単位。
それから
問題が発生する可能性があります：システム（1）では、最初の方程式は両方の部分を立方体に上げることによって得られました。これにより、追加の複雑なルートが表示されますか？ いいえ、あなたが表現すれば
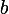を通して 元のシステムでは、すでに考慮されている二次方程式を取得します。 表現するとき を通して 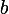同じことがあります。 これは、最後の集計の正義を証明します。
から立方根を抽出します
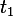そして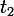 
複素数から根を抽出する規則によって。 ゲット
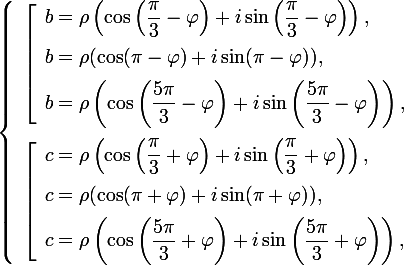
どこで
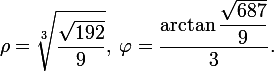
ペアを選択してください
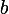そして そのため、複素数の虚数部のそれらの合計は0になり、実数部は負になります。 この場合、簡約式を使用します（方程式の残りの根を見つける必要がある場合は、三角関数の合計を製品に変換する式を使用することをお勧めします）。また、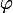 
第1四半期に属します。 それから
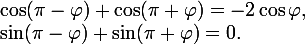
目的のルートはどこですか
三角関数のVieta式を使用すると、結果のルートはより単純な形式で記述されます
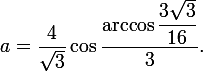
問題は、なぜカルダノの式を使用しなかったのかということです。 実際、学校では、3次方程式を解くために使用されると言われました。 その形式では、それは今やったことと似ています-最後に、複素数から立方根を抽出する必要があります。 ところで、複素数が最初に適用されたのは、3次の方程式を解くときです。
3次方程式の根の構成を決定するために、 判別式の概念が使用されます （2次方程式の場合のように）。 一般に、代数の判別式の概念は 、任意の次数の多項式に導入されます。
2. 3次方程式による物理的問題の例
雑誌「Quantum」で、私はかつて物理学における興味深い問題に出会い、3次方程式の解を見つけました。 一番下の行は次のとおりです。 最大速度を決定する必要があります
車の質量を開発することができます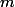 
（人と一緒に）既知の最大出力で 
エンジン？
車の最高速度では、関数の導関数が極値点で消失するため、その加速度はゼロです。 一定の速度で移動する場合はゼロですが。 それから私達はこれを言うことができる：車が開発できる最高の一定速度は何であるか。
高速では、空気抵抗は無視できなくなりますが、 抗力 はストークスの法則ではなく、2次の法則で表現されます。これは、移動速度が非常に速いためです。 次に、エンジンの牽引力は、空気抵抗力と、車のホイールのタイヤと車道の間に生じる転がりおよび滑りの摩擦力によってバランスがとられます。
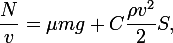
どこで
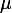-総摩擦係数、 
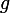-重力の加速、 
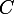- 空力抵抗係数 、 
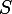-車の正面断面積。不完全な3次方程式が得られます。
3.質問と回答
トピックを読むときに、読者に質問があるかもしれません。 たとえば、次のとおりです。
1.なぜ著者は完全な三次方程式を考慮しなかったのですか？ 回答：完全な3次方程式は不完全な置換に還元されます
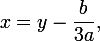
どこで
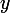新しい変数です 
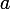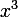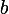-係数 
、 -係数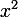 
。
2.トピックの冒頭で、4次の多項式が検討されました。 そのような方程式を解析的に解く方法はありますか？ 回答：はい、 フェラーリの方法があります。
3. Abel-Ruffiniの定理により、 4次以上の方程式はラジカルでは解けません。 そして、ここで、三角関数を含む三次方程式の根を取得します。これは、おそらくラジカルを通して表現できないでしょう。 回答：定理の記述では、根の一般的な表記法、つまり 計算式の係数を数式に代入することにより、複素数から根を抽出することもできます。
4. Evarista Galoisの後、任意の次数の方程式の根の公式を取得する試みはありましたか？ 答え：少し前まで、私はアメリカの数学者デイビッド・マンフォードによる本のロシア語の翻訳、「シータ関数の講義」（ミール、1988）に目をつけました。 さらに、Umemur Hiroshiの研究「シータ定数を使用した代数方程式の解法」が提供されています。ルート抽出関数は、シータ定数で表される別の関数、Siegelモジュラー関数に置き換えられます。 この作品はまた、ガロア後のこの問題の研究の歴史を強調しています。
5.私が理解するように、そのような式は、任意の次数の方程式を解くという実際的な問題での使用には適用できません。 近似根を取得するためのアルゴリズムの説明を含む現代の作品はありますか？ 回答：G.P.の本に助言します。 Kutishcheva「任意の次数の代数方程式の解法：理論、方法、アルゴリズム」（URSS、2010年）。
6.数値ニュートン法の現代的な修正はありますか？現在、方程式や方程式系の近似解を得るための主要な方法です。 回答： Janak Raj Sharma、Rangan Kumar Guha、およびRajni Sharmaによる記事「非線形方程式のシステムのための効率的な4次加重ニュートン法」をご覧ください。
7.根の解析式を取得することが可能な高度の方程式の特別なケースはありますか？ 回答：5次方程式の実際の解を見つけるためのルーリングと、任意次数の不完全な方程式のためのローレンスグラッサーの公式をもたらします。
結論として、初心者にはS.L.という本をお勧めします。 タバチニコワとD. B. フックス「数学的転換」（ICMMO、2010）。