その結果、従来のアルゴリズムでは達成できない興味深い結果が可能になることがわかりました。 たとえば、攻撃者が衝突を簡単に検出できないハッシュ関数を構築できます。 または、番号が元のセットに属していることを確認する機能を保持しながら、多数の番号を処理して何度も圧縮します。 わずかなメモリを追加するだけで、データストリーム内のさまざまな要素の数を概算できます。 この講義では、マキシム・バベンコは小学生にこれがどのように起こるかを伝えます。
ハッシュ関数
コンピューターサイエンスでは連想表と呼ばれるデータ構造を考えたいとします。 この表では、コンポーネントのペアが2列に記載されています。 最初の列はキーと呼ばれ、2番目の列は値です。 たとえば、キーは人の名前であり、値は彼の住所です。 私たちのタスクは、このテーブルですばやく検索を実行することです。特定のキーが存在するテーブルの行を見つけ、対応する値を提供します。 テーブル全体を上から下に表示するオプションは、すばやく検索するため、私たちには適していません。 テーブルの行数をnとすると、検索時間はnより大幅に短くなります。 テーブル内のすべてのキーは一意であると考えています。 キーが整数の場合、すべてが非常に単純になります。 0からm-1の範囲の可能なキー値によって要素がインデックス付けされる配列を作成する必要があります。ここで、mは大きすぎません。 このデータストレージの方法では、キーkを使用して対応する行にアクセスし、対応する値を見つけるために、一定の時間O(1)を費やす必要があるため、このアプローチは優れています。 この方法の欠点は、たとえば数字の代わりに文字列をキーとして使用する場合、これらの文字列を数字でエンコードする必要があることです。 そして、このようなコーディングでは、数値範囲が広すぎます。
そして、ここでハッシングが役立ちます。 サイズmのテーブルがまだあると仮定しますが、今回はmが所有するキーとは関係ありません。 鍵はいくつかの整数です。 これらの条件下で、テーブル内のキーkの位置をどのようにして見つけることができますか? ハッシュ関数と呼ばれる関数-h(k)を知っているとします。 与えられたkについて、mのうちのどのセルにこのキーが含まれているかがわかります。 ハッシュ関数の動作を考慮しない場合、すべてが非常に単純に見えます。 しかし、キャッチがあります。 まず、可能な限り多くのキー値があり、ハッシュ関数は有限集合にマッピングされます。 したがって、もちろん、ハッシュ関数を適用した後の2つの異なるキーが同じセルに落ちた場合、それらを同時に格納する方法は明確ではありません。 このような状況は衝突と呼ばれ、それらに対処できる必要があります。 戦う方法はたくさんあります。 最も単純だが同時に非常に効果的な方法の1つは、セルに値が含まれておらず、キーと値のペアでさえも、ペアのリスト全体が含まれていると考えることです。 これらはすべて、ハッシュ関数の影響下にあるキーが特定の値をとったペアです。 これは、チェイン方式による衝突解決と呼ばれます。
ここで重要なのは、ハッシュ関数の選択です。 これが効率に影響するものです。 h(k)= 0を選択した場合、すべてのハッシュはゼロに等しくなり、最終的には常に検索するチェーンが1つ得られます。 非常に遅く、採算が取れません。 しかし、ハッシュ関数の値が多少ランダムな場合、これは起こりません。
ランダムネス
数学の観点からランダム性の概念、またはむしろこの概念の離散バージョンを検討してください。 通常の六角キューブがあるとします。 それを投げて、ランダム性を生成します。 つまり 多くの基本的なイベントがあります-Ω。 私たちの場合、基本的なイベントは、キューブが完全に停止した後に一番上になる顔です。 面(a、b、c、d、e、f)を示します。 次に、確率分布を指定する必要があります。各基本イベントについて、その確率が0から1までであると言う関数を作成します。 なぜなら 立方体は滑らかで六角形なので、各辺から落ちる確率は1/6でなければなりません。
この場合のランダム変数は、基本イベントで定義された関数です。 キューブの面に1〜6の番号を付けた場合、ドロップされた面に対応する番号はランダム変数になります。
ここで、平均ランダム変数の概念を考えてみましょう。 当社の基本イベントがエンティティ(a 1 、...、a n )であり、それらに割り当てられた確率が(p 1 、...、p n )であり、関数が基本イベントを値(x 1 、...、x n )にマッピングする場合、次に、x 1 p 1 + x 2 p 2 + ... x n p nという形式の加重和を意味します。 つまり どの値とどの確率が受け入れられるかを調べてから、1つまたは別の基本イベントの発生確率に等しい係数で平均する必要があります。
マルコフ不等式
この補題の非公式の意味は次のとおりです。確率変数の平均が非常に大きくない場合、大きな値を取ることはできません。 問題の正式な声明と証拠を検討します。 離散確率空間(Ω、p)が与えられ、その上にランダム変数-f *Ω→R 1があるとします。 ランダム変数がε以上の値を取るような事件の可能性に興味があります。ここで、εは特定の正の数です。

証明に合格します。 証明された不等式は別の方法で書き換えることができます。
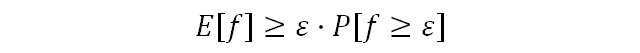
E [f] = x 1 p 1 + x 2 2 +⋯+ x n p nであることを思い出してください。 これから、次の結論を導き出すことができます。

最後まで講義を見てから、上記の構成が衝突の可能性が低いハッシュ関数を構築し、乱数を使用しないと不可能または効率が低い他のアルゴリズムタスクを実行するのにどのように役立つかについても学習します。