楽しい時間を!
「最適化入門」を読んでください。 シミュレーテッドアニーリング 。 」 たまたま偶然、巡回セールスマンの問題に出会い、それを解決するアルゴリズムを思いついたのですが、その本質は、この記事で説明したアニーリングシミュレーションアルゴリズムの概念に非常に近いものでした。 さらに、私のアイデアへの「参照」もあり、同様の議論がコメントで行われました。なぜなら、コミュニティが実装を見ることが面白いと判断したからです。
簡単な紹介から始めましょう。 私は専門の「ソフトウェアエンジニアリング」の1年生で、この学期には分散システムのコースがあり、そこでは実装のためのセールスマンの仕事がありました。 また、大丈夫ですが、4つの異なるテクノロジ(Windows Azure、openmpiライブラリ、Goプログラミング言語、OS InfernoのLimboプログラミング言語)を使用して並行して実装する必要もあります。 このようなよく説明された解決策に出くわした場合、問題ははるかに少なくなりますが、その時点では分岐限定法のみを検出できました。 それは並行して実装するというアイデアに加えて、以前は未知の技術を使用していたという考えがすぐに私には失敗したように思えたので、下劣なことを言わなければなりません。 この問題を長い間熟考した結果、あまり効果的ではないものの、驚くほど単純であることが判明したアルゴリズムに至りました。 それにもかかわらず、私はそれをなんとか先生に渡すことができ、アルゴリズムに関する実行された「研究」作業は、判明したように、この記事に非常に適しています。 記事を除いて、プログラムコードを純粋なC#で、並列トラブルを使用せずに提供します。
最適化とアニーリング方法とは何なのかについては触れません。記事「Introduction to Optimization。 シミュレーテッドアニーリング」それはうまく説明されており、より詳細に理解したい人は誰でもそれを読むことをお勧めします。 巡回セールスマンの問題と私の解決策の説明にまっすぐ進みます。
タスク分析
セールスマンのタスクは、最も有名な組み合わせ最適化タスクの1つです。これは、これらの都市を一度通過してから元の都市に戻る最も収益性の高いルートを見つけることで構成されます。 問題の状況では、ルートの収益性の基準(最短、最低、累積基準など)が示されます。
問題を形式化する場合、特定の重み付きグラフについて話します(説明を簡単にするために、無指向性にしますが、一般的なケースではそうではないかもしれません)。一方、最小ウェイト(詳細については、グラフの都市の頂点、エッジウェイト(都市間の距離)と呼びます)。
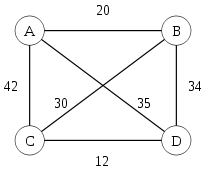
このようなグラフは、主対角線上にゼロがある対称行列として表すことができます(都市から都市までのパスの長さはゼロに等しい)。

決定アルゴリズム
このパートでは、アルゴリズムを実装する両方の方法(シリアルおよびパラレル)について説明し、シリアルバージョンのプログラムコードを提供します。
順次実装
すべての頂点を一度含む任意の開始パスを作成し、開始位置に戻ります。 次に、2つの都市をランダムに交換し、古いパスと新しいパスの長さを比較します。 新しいパスが短い場合は、保存します。 そうでない場合は、カウンターを増やします。 カウンターが所定の値をとるとき、アルゴリズムを停止します。この方法で見つかった最後のパスが最適と見なされます。
並列実装
すべての頂点を含む任意の初期パスを一度作成し、初期位置に戻り、各並列プロセス/フローに「分配」します。 それらはそれぞれ、互いに独立して、説明された操作を実行して最適なパスを見つけ、結果を返します。 暗黙の場合、メインスレッドは結果から最適なものを選択します。
ご覧のとおり、アイデアは非常にシンプルです。 驚くべきことに、シリアルバージョンとパラレルバージョンの両方で非常に簡単に実装されます。 2番目のケースでは、共有リソースに苦労することはなく、フロー自体の間で情報を交換することもありません。これにより、プログラミングが想像を絶するほどになります。
C#ソフトウェアの実装
class CCities { // public Point[] Coordinate; public CCities(int N, int maxValue) //maxValue - pictureBox { Random random = new Random(); Coordinate = new Point[N]; // , pictureBox, // int minBorder = (int)(maxValue * 0.05); int maxBorder = (int)(maxValue * 0.95); for (int i = 0; i < N; i++) { Coordinate[i] = new Point(random.Next(minBorder, maxBorder), random.Next(minBorder, maxBorder)); } } }
class CPath { // double[,] distance; // public int[] Path; public CPath(CCities map) { // distance = new double[map.Coordinate.Length, map.Coordinate.Length]; // , for (int j = 0; j < map.Coordinate.Length; j++) { distance[j, j] = 0; for (int i = 0; i < map.Coordinate.Length; i++) { double value = Math.Sqrt(Math.Pow(map.Coordinate[i].X - map.Coordinate[j].X, 2) + Math.Pow(map.Coordinate[i].Y - map.Coordinate[j].Y, 2)); distance[i, j] = distance[j, i] = value; } } // // 1 - , 0 - "" Path = new int[map.Coordinate.Length + 1]; for (int i = 0; i < map.Coordinate.Length; i++) { Path[i] = i; } Path[map.Coordinate.Length] = 0; } //, public void FindBestPath() { Random random = new Random(); for (int fails = 0, F = Path.Length * Path.Length; fails < F; ) { // // int p1 = 0, p2 = 0; while (p1 == p2) { p1 = random.Next(1, Path.Length - 1); p2 = random.Next(1, Path.Length - 1); } // double sum1 = distance[Path[p1 - 1], Path[p1]] + distance[Path[p1], Path[p1 + 1]] + distance[Path[p2 - 1], Path[p2]] + distance[Path[p2], Path[p2 + 1]]; double sum2 = distance[Path[p1 - 1], Path[p2]] + distance[Path[p2], Path[p1 + 1]] + distance[Path[p2 - 1], Path[p1]] + distance[Path[p1], Path[p2 + 1]]; if (sum2 < sum1) { int temp = Path[p1]; Path[p1] = Path[p2]; Path[p2] = temp; } else { fails++; } } } // public double PathLength() { double pathSum = 0; for (int i = 0; i < Path.Length - 1; i++) { pathSum += distance[Path[i], Path[i + 1]]; } return pathSum; } }
アルゴリズムの例


アルゴリズム性能分析
最初に、このようなアルゴリズムの並列化の効率を証明します。 各並列プロセスは同じ初期条件で動作を開始するため、それぞれの最適な解を見つける確率は同じになります。 pのためにそれを取る。 その場合、そのような解が見つからない確率はq = 1-pになります。 したがって、プロセスの少なくとも1つが最適なパスを見つける確率Pは次のようになります。
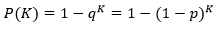
ここで、 Kは並行して実行されているプロセスの数です。 このような依存性は、小さいpでも非常に迅速に1になる傾向があります。 この図は、 p = 0.1の依存関係P(K)のグラフを示しています(「de jure」グラフは離散的である必要がありますが、そのような自由を許してください)。

すでにK = 6..7で、確率Pが0.5に等しくなることがわかります。 つまり、いくつかのプロセスを使用することの利点は明らかであり、確率が非常に急速に増加します。
ここで、1つのプロセスの確率pを見つけます。 明らかに、これは行列のサイズNに反比例し、アルゴリズムの動作が停止したときにカウンターが到達するFの値に直接比例します。 残念ながら、より正確な評価を行うことはほとんど不可能です。 グラフについて言えることはほとんど、異なるパスの数が(N-1)に等しいことです!⁄2 (1つの都市が開始都市であり、明らかに列挙に参加していないため、1つを減算しますが、同じパスを両方向で回避できることを確認してください)。
したがって、望ましい確率は実験的にのみ推定できます。 さまざまなパラメーターNに対して一連の実験が行われました。 カウンターの制限として、値F = N ^ 2が受け入れられます。 各Nに対して10,000回の実行が実行され、得られた結果が表にリストされています。

導入された表記法について説明します。
P(最小)は、最適な解を見つける確率です。 P(X%) -最適値とX%以下の差がある解を見つける確率。 つまり、たとえば、 P(10%)の場合、そのようなソリューションは[min、min +(max-min)* 0.1]の間隔に収まるソリューションになります。ここで、 minとmaxはそれぞれ見つかった最小パスと最大パスです。
ここで余談をしてこれを言う必要があります。 もちろん、このような分析は実際の正確さを装うわけではありません。なぜなら、10,000回の実験でも目的のパターンを取得するのは非常に少なく(結果を再起動すると、完全に異なることが判明する可能性があります)、そして最も重要なことは、アルゴリズムが真実を見つけたという保証がないことです可能な方法の最適。 評価のために、彼は発見された最高の知識に基づいて行動しますが、彼がすべての最高であるという事実からはほど遠いです。 それにもかかわらず、定量的ではなく、少なくともアルゴリズムの定性的理解のために、結果を使用することが可能であると信じています。
同じ結果を示します。

この方法の利点
- アルゴリズムの「イデオロギー」の単純さ。
- シリアルバージョンとパラレルバージョンの両方での実装の容易さ。
- 並列実装によるアルゴリズムの効率の急速な向上。
- 最適に近い解を見つける可能性が高い。
メソッドの欠点
- Nの増加とともに正確な解を見つける確率が非常に急速に低下します。
- 解決策を見つける確率を正確に評価することの難しさ。
- 並列バージョンのスレッド間の関係の欠如は、各スレッドが同じ悪い解決策を見つけて全体的な結果を最適化できないという事実につながります(非常に悪い運で、すべてのスレッドは各反復まで同じ仕事をして、1つと同じを返すことができます)最終的には同じ方法です。非常に可能性は低いですが、不可能ではありません)。
アルゴリズムの最適化
このメソッドの作業と研究の過程で、アルゴリズムを改善するための次の可能な方法を提案しました。
- 実証済みのパスの「履歴」を追加します。 現時点では、アルゴリズムはテストされたパスを記憶せず、各反復で受け取った新しいオプションを制御しません。 そのようなパスをチェックしてふるいにかける機能を追加すると、結果の精度に大きく影響するはずです。
- おそらく、カウンタ参照値をより細かく調整する方法があります。 テストグラフからわかるように、現在の設定( F = N ^ 2 )では、サイズN = 20の行列の領域に「穴」が表示されます。このグラフの動作の理由を正確に理解することはできませんが、この値をより適切な方法で選択する方法はおそらくあります。
おわりに
私は率直になります-それはまあまあ動作します。 すべてのグラフとその他の結果を示しましたが、作業の結果には多くの要望が残っていることがわかります。 いずれにしても、このアルゴリズムを使用して、この段階で正確な解を見つけることはできません。 一方で、彼はまだ多かれ少なかれ正気な選択肢を見つけており、率直なくだらないことに陥ることはありません。 タスクが正確なソリューションを必要としないが、最適なソリューションに近づいた場合、このアルゴリズムは非常に機能的です。 または、このアルゴリズムを使用して、最初に最適な値に近づいてから、オプションの列挙などを実行できます。
アルゴリズムを改善するためのアイデアをお持ちの場合は、それらを聞いて非常にうれしいです。
また、記事自体に対する建設的な批判(デザイン、プレゼンテーションスタイルなど)を聞く準備ができています。
コードを掘り下げたい人のために、メールクラウドにプロジェクトと共にアーカイブを投稿しました(VS2012で記述されたプロジェクトは、VSの以前のバージョンと互換性がありません。プログラムを実行するには、.netフレームワーク4.5が必要になります。デバッグ)