ポアソンプロセスのモデリング

はじめに

自然界で観察される最も重要なプロセスの1つは、ポアソンポイントプロセスです。 したがって、このようなプロセスをモデル化する方法を理解することが重要です。 モデリング方法は、ポアソンポイントプロセスのタイプ、つまり、プロセスが行われる空間、およびプロセスの均一性または不均一性によって異なります。 ポアソンポイントフローの開発や、さまざまな分野での重要なアプリケーションには興味がありません。 この資料を興味深いものにするために、読者は基本理論についてはFeller（1965）およびSinlar（1975）の関連するセクションを、ITアプリケーションについてはTrivedi（1982）のいくつかのセクションを読むことをお勧めします。



最初のステップでは、[0; +∞）でポアソンプロセスを定義します。 プロセスは、特定のランダムな時間に発生するランダムイベントのファミリーによって完全に決定されます0 <T1 <T2 <... N（t1、t2）が時間間隔（t1、t2）の間に発生したイベントの数である場合、多くの場合、次の2つの条件が満たされます。

• 互いに素な間隔（t1、t2）および（t3、t4）では、ランダム変数N（t1、t2）およびN（t3、t4）は独立しています。
• N（t1、t2）はN（0、t2-t1）と同様に分布します。つまり、特定の時間にわたるイベント数の分布は、この間隔の長さのみに依存します。

驚くべき事実は、これらの2つの条件は、すべての確率変数N（t1、t2）がポアソンの法則に従って分布し、N（t、t + a）が法則Po（λa ）非負のtおよびa> 0の場合。 たとえば、Feller（1965）を参照してください。 したがって、ポアソン分布は非常に自然に発生します。



前の概念は、R ^dに一般化できます。 AをR ^dのサブセットとし、Nを整数値のみを取るランダム変数とします。 X ₁ 、... X _NをAの値を取るランダムベクトルのセットとします。次に、X _iがAの均一または均一なポアソンプロセスを定義するとします。

• 有限体積の集合A A _iのペアワイズ素集合の有限集合の場合、イベントN（A ₁ ）、...、N（A _kは独立
• AのボレルサブセットBの場合、N（B）の分布はBの体積のみに依存します。

翻訳者注：「メジャー」という言葉を使用する方が良いでしょうが、数学に熱心でない人にとっては、1ダース以上のページを説明する必要があります。



繰り返しますが、これらの仮定は、すべてのN（B）が法則P（λVol（B））に従って分布することを必要とします。これは強度またはAの均一ポアソン過程の強度パラメーターと呼ばれます。ペトリ皿上の細菌とヒューストンの殺害が含まれます。

均一ポアソンプロセスのモデリング

R _dに属する集合Aで均一なポアソンプロセスをモデル化する必要がある場合、Aから多数のランダムベクトルX _iを生成する必要があります。定理1.1により、これは次のように実行できます。



N λVol(A)





X1,..,XN,





RETURN 1,...,N







Nの値を生成するには、アルゴリズムの最後に少なくともΩ（n）の操作を費やすため、平均複雑度O（1）のアルゴリズムを使用しても意味がありません。 したがって、このアルゴリズムを使用する場合は、非常に単純なアルゴリズム（ポアソン確率変数を生成することを強くお勧めします（平均時間はO（λ）になります））。 特定のセットAについては、ポアソン確率変数の明示的な生成を必要としない他の方法を使用できます。 これを説明するために使用する3つのケースがあります。

1. A = [0; +∞）
2. A-サークル
3. A-長方形

これを行うには、ポアソン過程と指数分布の間の興味深い関係が必要です。





定理1.2は、A = [0; +∞）で均一なポアソン過程をモデル化するための次の方法を提供します。



T = 0 ( "")





k = 0 ( )





REPEAT











k = k + 1





T = T + E/λ





T[k] = T





UNTIL ( ; )







このアルゴリズムは、ポアソン確率変数を生成する必要がないため、実装が簡単です。 他の単純な集合Aについては、定理1.2の簡単な一般化があります。 たとえば、A = [0、t] x [0,1]の場合、tは無限大に等しく、0 <T1 <T2 <...は強度λの一様なポアソン過程で、U1、U2、... [0,1]ランダム変数、次に（T1、U1）、（T2、U2）、...は、Aの強度λでポアソン過程を決定します。

例1.1。

単位円上の均一ポアソン過程

Aが単位半径の円である場合、均一なポアソンプロセスのさまざまなプロパティを使用して、いくつかの生成方法（d次元の球体に一般化）を取得できます。 λを希望の強度にします。

まず、パラメーターλπでランダムなポアソン値Nを生成し、次に単位円上に均等に均等に分布したN個の独立したベクトルのシーケンスを返します。 定理1.2で提案された順序統計の方法を適用すると、ポアソン確率変数が暗黙的に取得されます。 たとえば、極座標（R、φ）に進むと、一様なポアソンプロセスの場合、Rとφは独立しており、ランダム変数Rの密度は2rであり、rは0から1に変化し、φは[0;2π]に均等に分布しています。 したがって、次のように進めることができます：均一なポアソンプロセス0 <φ1<φ2<... <φNを生成し、指数法により[0;2π]の強度パラメーターλ/（2π）を返し、（φ1、R1）、...、 （φN、RN）、ここでRiは[0; 1]の密度が2rの独立して同一に分布するランダム変数で、[0; 1]に均一に分布する最大2つの独立ランダム変数を取ることで生成できます。 指数メソッドをコーナーに適用する特別な理由はありません。 同様に、半径を取得できます。 残念ながら、順序半径は[0; 1]で1次元の均一ポアソンプロセスを形成しません。 しかし、それにもかかわらず、それらは不均一なポアソン過程を形成し、そのような過程の生成は次のセクションで検討されます。

不均一ポアソン過程

イベントが「ランダムな時間」に発生する状況もありますが、ある瞬間は他の瞬間よりも可能です。 これは、集中治療センターへの到着、コンピューターセンターでの求人、NHLプレーヤーの負傷の場合です。 これらの場合、非常に良いモデルは、不均一ポアソンプロセスのモデルであり、ここでは便宜上[0; +∞）で定義されています。 これは最も重要なケースです。なぜなら、時間はほとんどの場合「実行変数」だからです。

[0; +∞）の不均一ポアソンプロセスは、非負の定強度関数Λ（t）によって決定されます。これは、[0; +∞）上の積分が必ずしも1に等しくない（通常、発散する） ） プロセスは、次のプロパティによって決定されます：互いに素な間隔A1、A2、...、Akの有限コレクションの場合、これらの間隔（N1、...、Nk）で発生するイベントの数は、パラメーターを持つ独立したポアソン確率変数です



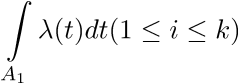
次に、このようなプロセスをどのようにモデル化できるかを検討します。 モデリングでは、イベントが発生する時間、0 <T1 <T2 <...を昇順で指定する必要があることを理解しています。 異種ポアソンプロセスのモデリングに関する多くの作業は、ルイスとシェドラー（1979）によって行われました。 このセクション全体は、彼らの仕事の改訂版です。 連続ランダム変数を生成する一般原則が拡張できることを観察することは興味深いです。反転、偏差、および合成の方法による類似物があることがわかります。

分布関数の役割は、統合された強度関数によって引き受けられます



T _n = Tの場合、T _{n + 1} -T _nには分布関数があることに注意することから始めます。



関数Λ（t）がtの増加とともに無制限に増加する場合。 これは、







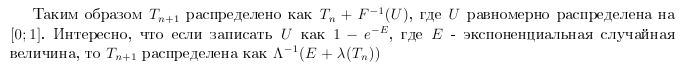
つまり、Λを反転させる必要があります。 正式には、強度関数の積分の逆に基づくアルゴリズム（Sinlar（1975）またはBretley、Fox、およびSchrage（1983）も参照）があります（反転法）



T = 0 ( )





k = 0 ()





REPEAT





E





k = k+1





T = T + InvΛ(E+Λ(T)), (InvΛ - Λ)





T[k] = T





UNTIL False

例1.2 均一ポアソン過程

特殊なケースλ（t）=λ、Λ（t）=λtの場合、InvΛ（E +Λ（T））= T + E /λであることが簡単にわかります。その結果、指数関数法を再度取得します。

例1.3

ラッシュアワー前の朝の車の流れをシミュレートするために、時々λ（t）= tを取り、次にΛ（t）= t ^ 2/2を取り、ステップを取得することができます



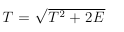
強度関数が強度関数の合計として表現できる場合、つまり 、



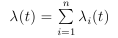0 <T _i1 <T _i2 <... T _inは、個々の不均一ポアソンプロセスの独立した実装であり、結合された順序付きシーケンスは、強度関数λ（t）を持つ不均一ポアソンプロセスの実装を形成します。 これは合成メソッドにも適用されますが、現在の違いは、すべてのプロセスコンポーネントの実装が必要なことです。 分解は、分析形式λ（t）によって決定される自然な分解がある場合に使用できます。 プロセスのマージの主な操作はn個のプロセスから最小値を取得することであるため、n個の要素のヒープに時刻を格納することでnが大きくなる利点が得られます。



結果として、合成メソッドを取得します。



T[1,1],...,T[n,1] n





T = 0 ( )





k = 0





REPEAT





T[i,j]





k = k + 1





T[k] = T[i,j]





T[i,j+1]





UNTIL False







3番目の一般原則は、間伐の原則です（Lewis and Shedler、1979）。 偏差法で起こることと同様に、任意のtに対してわずかな支配的な強度関数λ（t）<=μ（t）があると仮定します。



次に、アイデアは、0とμ（t）の間の正の半平面の部分で均質なポアソン過程を生成し、λの下で均質なポアソン過程を考慮し、最後に、この過程でイベントのx成分を返すことです。 これには次の定理が必要です。









次に、ルイスとシェドラーを間引く方法を考えます。



T = 0





k = 0





REPEAT





Z, μ, T. T = Z





[0;1] U





IF U <= λ(Z)/μ(Z)





THEN k = k + 1, X[k] = T





UNTIL False







そのように生成されたシーケンスX _kは、強度関数λで不均一なポアソン過程を形成すると主張されています。 強度関数μで不均一プロセス0 <Y1 <Y2 <...を取り、いくつかの点を削除したことに注意してください。 私たちが知る限り、（Y _i 、U iμ（Y _i ）は、定理1.3によりU 0が[0; 1]に一様に均一に分布する独立したランダム変数である場合、曲線上の単位強度をもつ均一ポアソン過程です。曲線λは、この曲線上に単位強度を持つ均質なポアソン過程を定義します（定理1.3のパート3.）最後に、このサブシーケンスのみのx座標を取得すると、強度関数λを持つ不均一なポアソン過程が得られます。

通常、強度関数μをもつ不均一ポアソン過程は、反転法によってモデル化されます。

例1.4 周期強度関数

次の例もLewis and Shedler（1979）に属します。 周期関数λ（t）=λ（1 + cos（t））を持つ関数を考えて、支配的な関数μ=2λを選択します。



次に、シミュレーションアルゴリズムは次の形式を取ります。



T = 0





k = 0





REPEAT





E c 1





T = T + E/(2λ)





[0;1] U





IF U <= (1+cos(T))/2





THEN k = k + 1, X[k] = T





UNTIL False







言うまでもなく、2人の警官の定理を使用して、ほとんどの場合、コサインの計算を回避できます。



不均一なポアソン過程が集合[0、t]でモデル化されるときのアルゴリズムの有効性に関する最後の言葉。 支配的なプロセスから必要なイベントの平均数は 返されるランダム変数の平均数は

平均値の比は、標準偏差法の偏差定数の精神に匹敵する、効率の客観的な尺度と見なすことができます。 一般的な場合、単一の値が返されないという正の確率のために、無限大に等しいため、比率の平均値を使用できないことに注意してください。