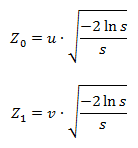
ここで、Z 0とZ 1は目的の値、s = u 2 + v 2 、uとvは区間(-1、1)に一様に分布するランダム変数で、0 <s <1の条件を満たすように選択されています。
多くの人は考えずにこれらの式を使用し、多くは既製の実装を使用しているため、その存在を疑っていません。 しかし、質問がある人もいます。「この式はどこから来たのですか? そして、なぜ一度に数個の数量を取得するのですか?」 次に、これらの質問に明確な答えをしようとします。
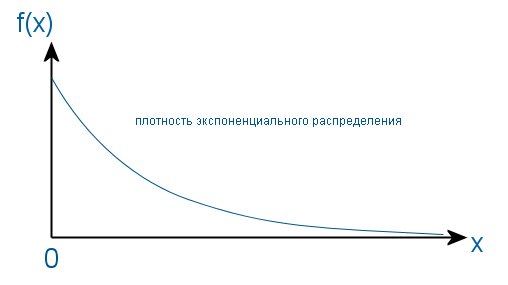
まず、確率密度、確率変数の分布関数、逆関数が何であるかを思い出させてください。 分布が密度関数f(x)によって与えられる特定のランダム変数があり、次の形式があるとします。
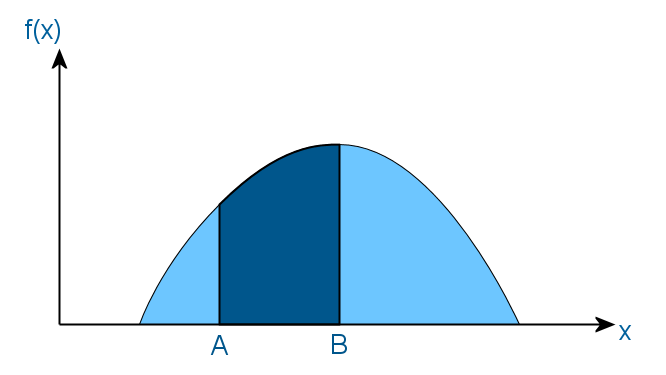
これは、この確率変数の値が間隔(A、B)にある確率が、影付き領域の面積に等しいことを意味します。 そして、その結果、いずれの場合でも、ランダム変数の値は関数fの定義の領域に入るため、影付き領域全体の面積は1に等しくなければなりません。
確率変数の分布関数は、密度関数の積分です。 この場合、おおよその形式は次のようになります。
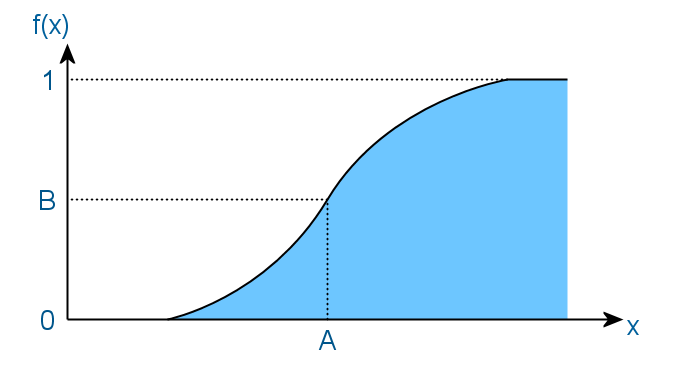
ここでのポイントは、確率変数の値が確率BでAよりも小さくなることです。その結果、関数は決して減少せず、その値は区間[0、1]にあります。
逆関数は、元の関数の値が渡された場合に元の関数の引数を返す関数です。 たとえば、関数x 2の場合、ルート抽出関数は逆になり、sin(x)の場合はarcsin(x)などになります。
出力のほとんどの疑似乱数ジェネレーターは均一な分布のみを提供するため、多くの場合、他のジェネレーターに変換する必要が生じます。 この場合、通常のガウスでは:
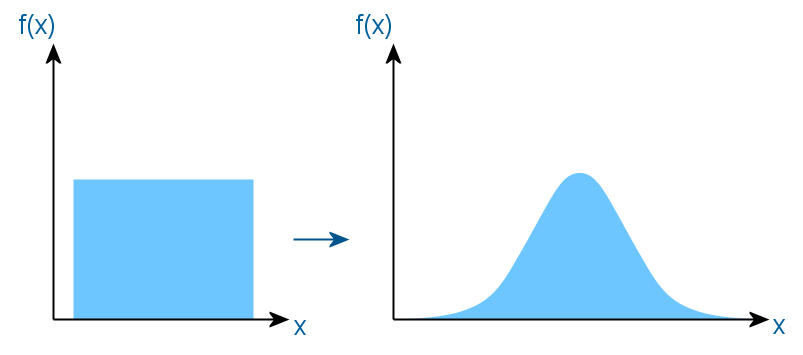
一様分布を他の分布に変換するすべての方法の基礎は、逆変換方法です。 次のように機能します。 必要な分布の関数と逆の関数が見つかり、間隔(0、1)に一様に分布したランダム変数が引数として転送されます。 出力では、必要な分布で値を取得します。 明確にするために、次の図を引用します。

したがって、均一なセグメントは、新しい分布に従って塗りつぶされたようになり、逆関数を介して他の軸に投影されます。 しかし問題は、ガウス分布の密度の積分を計算するのが簡単ではないため、上記の科学者はだまされなければならなかったことです。
カイ二乗分布(ピアソン分布)があります。これは、k個の独立した正規確率変数の二乗和の分布です。 また、k = 2の場合、この分布は指数関数的です。
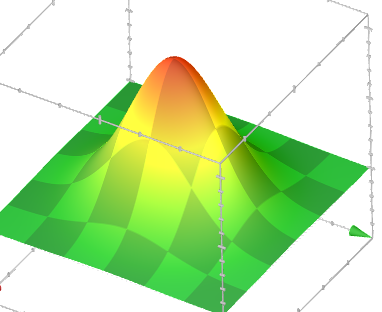
これは、直交座標系の点にランダムなXおよびY座標が正規分布している場合、これらの座標が極座標系(r、θ)に転送された後、半径の2乗(原点から点までの距離)は指数関数的に分布し、半径の二乗は座標の二乗の合計であるため(ピタゴラスの法則による)。 平面上のそのような点の分布密度は次のようになります。
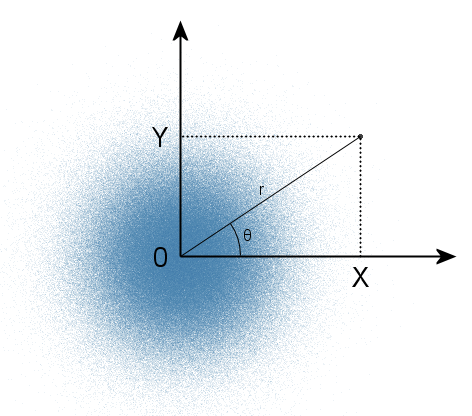
すべての方向で同等であるため、角度θは0から2πの範囲で均一に分布します。 逆もまた真です。2つの独立したランダム変数(均一に分布した角度と指数関数的に分布した半径)を使用して極座標系のポイントを指定すると、このポイントの直交座標は独立した通常のランダム変数になります。 そして、同じ逆変換方法を使用して、一様分布から指数分布を取得することはすでにはるかに簡単です。 これがポーラーボックスミュラー法の本質です。
次に、公式を導き出します。
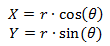 (1)
(1)
rとθを取得するには、区間(0、1)に均一に分布する2つのランダム変数を生成する必要があります(uとvと呼びます)。そのうちの1つの分布(たとえばv)を指数に変換して半径を取得する必要があります。 指数分布関数は次のとおりです。
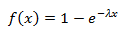
逆関数:
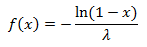
一様分布は対称的であるため、同様に、変換は関数で機能します
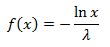
カイ二乗分布の式から、λ= 0.5になります。 λ、vをこの関数に代入し、半径の2乗を取得してから、半径自体を取得します。
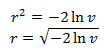
単位セグメントを2πに引き伸ばすことで角度を取得します。
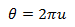
ここで、式(1)のrとθを代入して、次を取得します。
 (2)
(2)
これらの数式はすぐに使用できます。 XとYは独立しており、通常1の分散と0の数学的期待値で分布します。他の特性を持つ分布を得るには、関数の結果に標準偏差を掛けて数学的期待値を加算するだけで十分です。
ただし、角度を直接設定するのではなく、円のランダムな点の直交座標を介して間接的に設定することにより、三角関数を取り除く機会があります。 次に、これらの座標を使用して、半径ベクトルの長さを計算し、xとyをそれぞれ分割して余弦と正弦を見つけることができます。 どのように、なぜ機能するのですか?
円に均一に分布する単位半径からランダムな点を選択し、この点の半径ベクトルの長さの二乗を文字sで示します。
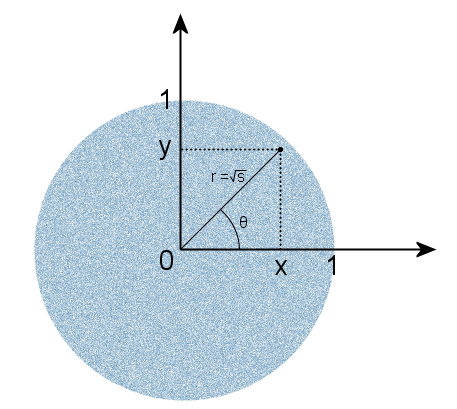
選択は、ランダムな直交座標xおよびyを設定し、間隔(-1、1)に均一に分布し、円に属さない点と、半径ベクトル角が定義されていない中心点を破棄します。 つまり、0 <s <1の条件を満たす必要があり、平面上のガウス分布の場合と同様に、角度θは均一に分布します。 これは明らかです。各方向のポイントの数は同じです。つまり、各角度が等しくなる可能性があります。 しかし、それほど明白ではない事実があります-sは均一な分布を持ちます。 結果のsとθは互いに独立しています。 したがって、3番目のランダム変数を生成せずにsの値を使用して指数分布を取得できます。 ここで、vの代わりにsを式(2)に代入し、三角関数の代わりに、座標を半径ベクトルの長さ(この場合はsのルート)で割って計算します。

記事の冒頭にあるように、数式を取得します。 この方法の欠点は、円に含まれていないポイントが拒否されることです。 つまり、生成されたランダム変数の78.5%のみを使用します。 古いコンピューターでは、三角関数が存在しないことで大きな利点が得られました。 さて、瞬時に1つのプロセッサコマンドがサインとコサインの両方を計算するとき、これらの方法はまだ競合できると思います。
個人的には、さらに2つの質問があります。
- sの値がなぜ均等に分配されるのですか?
- 2つの正規確率変数の平方和が指数関数的に分布するのはなぜですか?
sは半径の2乗(簡単のため、ランダムポイントの位置を設定する半径ベクトルの長さと呼ぶ半径)であるため、最初に半径がどのように分布しているかを調べます。 円は均一に塗りつぶされているため、半径rの点の数は半径rの円周に比例することが明らかです。 また、円周は半径に比例します。 これは、半径分布密度が円の中心から端に向かって均一に増加することを意味します。 また、密度関数の形式は、間隔(0、1)でf(x)= 2xです。 係数2。グラフの下の領域が1に等しくなるようにします。 そのような密度を二乗すると、均一な密度になります。 理論的にはこの場合、このためには、密度関数を変換関数の導関数で除算する必要があります(つまり、x 2から)。 そして視覚的にこれは次のように起こります:
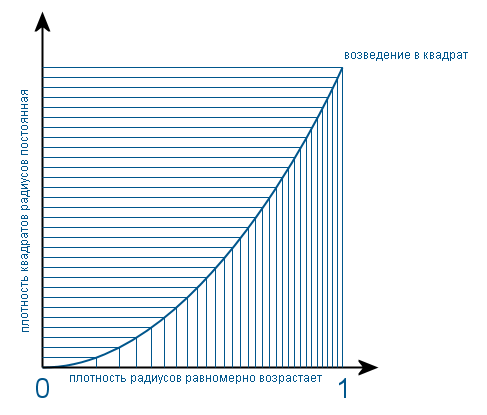
通常のランダム変数に対して同様の変換が行われた場合、その平方の密度関数は双曲線に似ていることがわかります。 そして、通常のランダム変数の2つの正方形の追加は、すでに二重積分に関連するはるかに複雑なプロセスです。 そして、結果が指数分布であるという事実は、私は個人的にここで実用的な方法で確認するか、公理として受け入れる必要があります。 そして、気にする人は、これらの本の知識を利用して、トピックをより身近に理解することを提案します。
- ベンツェルE.S. 確率論
- クヌートD.E. プログラミングの芸術、第2巻
結論として、JavaScriptで正規分布した乱数のジェネレーターの実装例を示します。
function Gauss() { var ready = false; var second = 0.0; this.next = function(mean, dev) { mean = mean == undefined ? 0.0 : mean; dev = dev == undefined ? 1.0 : dev; if (this.ready) { this.ready = false; return this.second * dev + mean; } else { var u, v, s; do { u = 2.0 * Math.random() - 1.0; v = 2.0 * Math.random() - 1.0; s = u * u + v * v; } while (s > 1.0 || s == 0.0); var r = Math.sqrt(-2.0 * Math.log(s) / s); this.second = r * u; this.ready = true; return r * v * dev + mean; } }; } g = new Gauss(); // a = g.next(); // b = g.next(); // c = g.next(); //
平均(平均)およびdev(標準偏差)パラメーターはオプションです。 対数が自然であることに注意してください。