
すぐに、シミュレーションはCAB WMで実行されることに注意してください。これは最初の記事で(それほど前ではないが)使用しました。
離散確率変数
2ダイスモデルの例を使用して、確率理論と数学的統計について少し話しましょう。 そのため、私たちはカジノのプレイテーブルで典型的な状況をプレーするという課題に直面しています。「いくつかのイベントを同時にプレイし、数字で2つのサイコロを投げます。 引き分けの結果に応じて、2番と4番の同時ヒット数を見つけます。 さらに、この単純なプログラムにハイライトがあるように、私たちはまだ例外処理に苦労しています。
2ダイスを投げる 

ご覧のとおり、すべてが非常に透過的であり、コードの大部分はこれらのアクションで占められています...プログラムの結果を見てみましょう。
クラッツ 
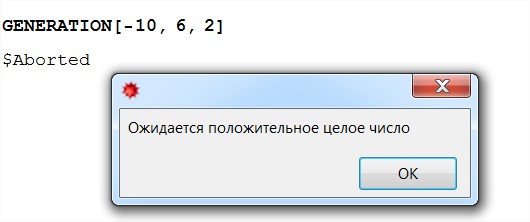


10個のイベントのサンプルで2と4の「トリプル」損失は排他的なケースであり、確率はほとんどありません。
したがって、以下のアルゴリズムに従ってWMを使用して擬似ランダムな離散値を再生しました。
アルゴリズム
- 間隔(0,1)をn-長さが等しい間隔に分割する必要があります
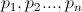 それに応じて。
それに応じて。 - 標準ランダム変数の値を再生します
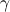 (標準MSS )。
(標準MSS )。 - 値をヒットする条件を確認します
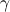 longのi番目の間隔で
longのi番目の間隔で  :
:  。
。
不等式が真の場合、この間隔に対応する値をランダム変数χに割り当てます。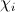
- 必要に応じて、標準値γの新しい値を使用して手順1〜3を数回繰り返し、確率分布の法則で離散確率変数の他の値を取得します。
ノイマン法
次に、約束されたように、ノイマン法により、必要な確率密度で連続ランダム変数を再生します。 ノイマン法に加えて、重ね合わせ法と逆関数法もありますが、それらについての話はこの記事の目的ではありません。 そこで、次のタスクを設定します。「Neumannメソッドを使用して、分布密度を持つランダム変数を再生します。
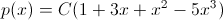 間隔x(0,1)で。」
間隔x(0,1)で。」
通常、物理学者はそのようなことを自動化するのではなく、事前にすべてを計算してから、単純にループを実行してサンプルを取得します。 私は、21世紀の物理学者として、強力なコンピューター代数システムを武器として、プロセスを自動化しようとしました。 その結果を見てみましょう。
ノイマン 

本のように、すべてが非常にシンプルであることがわかります。 私が注意したい唯一のことは、クォーク反クォーク消滅などの必要な確率密度である可能性がある単調に増加または減少する関数の場合、厳密性なしでノイマン定数の最適値の検索を組織することはほとんどの場合失敗することです セグメントの端の値は常に増加します。これはWM警告によってマークされ、その結果、プログラムブロックに統合することはできません。 正規化定数cは 、条件から計算されます
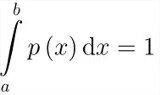
ノイマンアルゴリズム
この方法は、数学的統計と確率理論からの次の定理に基づいています。 させて  区間a <x <bの分布密度p(x)≤c( cは正の数)の確率変数です。
区間a <x <bの分布密度p(x)≤c( cは正の数)の確率変数です。  そして
そして 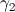 -独立したランダム変数
-独立したランダム変数 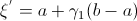 、
、  その後、ランダム変数
その後、ランダム変数  条件によって定義されます:
条件によって定義されます: 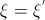 もし
もし  そして、p(x)に等しい確率密度を持ちます。
そして、p(x)に等しい確率密度を持ちます。
 区間a <x <bの分布密度p(x)≤c( cは正の数)の確率変数です。
区間a <x <bの分布密度p(x)≤c( cは正の数)の確率変数です。 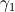 そして
そして 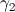 -独立したランダム変数
-独立したランダム変数 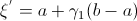 、
、  その後、ランダム変数
その後、ランダム変数  条件によって定義されます:
条件によって定義されます: 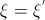 もし
もし  そして、p(x)に等しい確率密度を持ちます。
そして、p(x)に等しい確率密度を持ちます。
- 値のペアを取得します
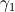 、
、 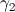 PHCの助けを借りて。
PHCの助けを借りて。 - それらを使用して、2つの乱数を作成します
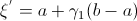 間隔(a、b)に均等に分散し、
間隔(a、b)に均等に分散し、  間隔(0、c)に均一に分布
間隔(0、c)に均一に分布 - 構築された数値を使用して、条件を検証します

- 条件が満たされている場合、確率変数の値は
 等しい
等しい 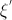 条件が満たされない場合、
条件が満たされない場合、
その後、手順1からの手順を繰り返します。
次に、この方法で10キロのイベントを生成し、ヒストグラムを作成し、同時にそれを必要な確率密度と比較します
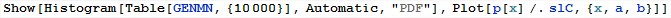 。
。
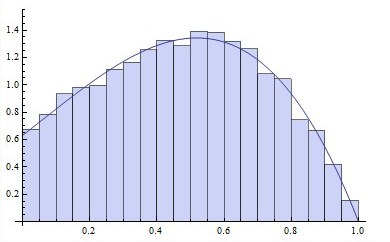
ご覧のとおり、結果はすべての期待を超えています! このアプローチの有効性は、一連の標準乱数(
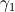 、
、 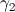 、...、
、...、  )は破棄されず、受け入れられます。 ノイマン法の場合、それを見つけるのは簡単です
)は破棄されず、受け入れられます。 ノイマン法の場合、それを見つけるのは簡単です 
コンプトン光子散乱
この記事の最後の部分に進み、MMKがPECでどのように機能するかを見てみましょう。 これを行うために、私たちは荒野に登るつもりはありませんが、学校の他の誰もが知っている電子によってガンマ量子を散乱させるプロセスをシミュレートします。 車輪を再発明しないために、CERNにアクセスするか、Geant4セクションに移動し、良心のtwin責なしに、物理学マニュアルのバトラーの分解(はい、はい、私が見逃したのと同じ)を書き、二次角のエネルギーと余弦を計算するための式を追加しますLSC内のパーティクル。 私は計算を行わず、コピーペーストを行いません。 すべてがアルゴリズムに含まれます。
コンプトン散乱 

このプロセスの微分断面積は、Klein-Nishinaの式で表されます。これは、まさに必要な確率密度です。
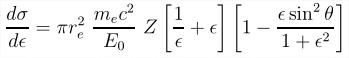
10キロのイベントを実行し、それぞれ0.5 MeVと1.5 MeVの2つのエネルギーの二次粒子のエネルギーと角度分布を構築します。


指で推定できるため、すべてが非常によく考慮されており、プロセスの運動学に対応しているため、この方法は非常に優れています。
おわりに
詳細をお伝えしたいと思いますが、この大ボリュームは、興味のある人だけが退屈すると思うと思います。文学を探すでしょう。CERNから引き出したマニュアルに書かれており、先生からも良いです。本で。 すべての計算は、自然の微積分システムと実験室の座標システムで実行されました。
文学
- geant4.web.cern.ch/geant4/G4UsersDocuments/UsersGuides/PhysicsReferenceManual/html/PhysicsReferenceManual.html
- Andreev、V. V.「素粒子物理学におけるモンテカルロ法」。 2005年の特別コースのカリキュラム。-15ページ。
参照資料
Wolfram Mathematica 9.0で使用される