🍟 🍆 🦋 ジュリアセットの構築 🔱 🌌 🤛🏾

こんにちは情熱が沸き、年末、セッション、締め切り、新年、検閲がインターネットのすべての層に浸透します。ハブルはもはやケーキではありません。私はこのアプローチに同意しないことを書きたかっただけですが、その後は禁止されます。したがって、興味深いコンテンツを作成する必要があります。ジュリアのセットに関する記事の紹介のために禁止されている場合は、まあ、ケーキの残りが落ちており、チャンスはありません。

それでは、投稿のトピックに戻りましょう。マイナス1の根がiであるだけでなく、複素数についてもう少し詳しく知りたいと思っていました。特に興味深いのは、フラクタル構造を持つ人物です。これが何を意味し、どのように視覚化するかを理解したかったのです。棚のどこかにTFKPに関する本があり、カーソルに関する複雑な分析のコースが終了し、少し自由な時間が現れました。始めましょう。

関数の反復

アルゴリズムを書く前に、いくつかの基本的な概念を学ぶ必要があります。関数fを反復するという概念から始めます。 fの n番目の反復に対して次の表記法を導入します。

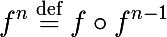
ここで、 ○は機能の構成です

IDマッピングはゼロ反復として取得されます。

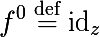
特定のタイプのマッピングの不動点には多くの定理があります。いくつかのマッピングgの不動点を思い出してください。これは次の方程式の解です。

同様に、関数の反復に対して、関数fの反復のシーケンスがマップfの固定点に収束するような関数fの領域からの点などの誘引点が導入されます。

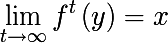
ここで、 yはxに十分近い点です

前の条件を満たすすべてのyの集合は、関数fの反復の下での点xの極限集合と呼ばれます。

原則として、反復によって形成される関数のシーケンスを調べることは興味深いです（同様の考えはニュートン法で見ることができ、望ましい解は構築されたマップの魅力的な固定点であることが判明しているため、反復シーケンスの制限として見つけることができます）。

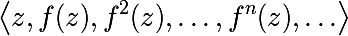
開始点で計算された一連の値

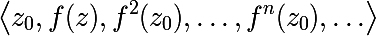
複雑な世界では、関数fの反復の下で点yからxへの反復収束を視覚化することは少し問題があり、すべて同じ4dですが、実際の世界では画像は2dだけです（赤の経路が発散し、青が固定点に収束します）。

それで、ジュリアのセットを理解するために必要な最初の小石が置かれました。次へ進みましょう。

二次複素多項式

一般に、ジュリア集合は次の形式の関数用に構築されます

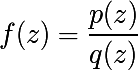
ここで、 pとqは複素多項式です

問題を単純化し、二次多項式に対してのみジュリア集合を構築します。一般形式の2次複素多項式は次のとおりです。

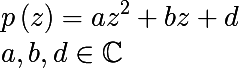
二次多項式のユニタリー（ a = 1 ）中心（ b = 0 ）形式の概念もあります

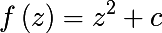
次のマップφを導入し、その逆マップを見つけます。

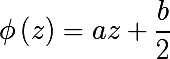
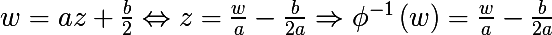
次の式を考えてください

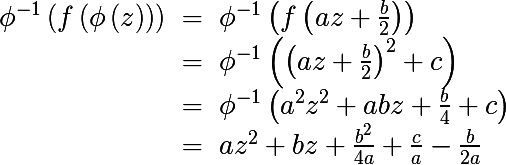
最後の式が一般形式p（z）の 2次多項式に似ていることは簡単にわかります。結果の式が一般形式の2次多項式に縮小されるようなcを見つけましょう。

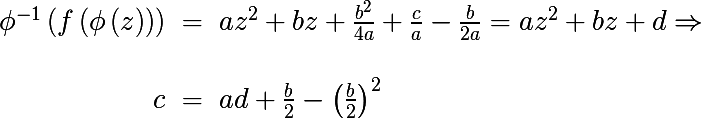
したがって、上記のcの置換により、一般形式の多項式は次のように記述できることを示しました。

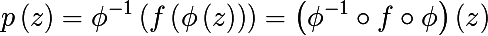
反復の作用下での二次多項式の振る舞い

ジュリア集合を理解するために、ベースの3番目の小石に移りましょう。複素2次多項式の2回目の反復を考えます

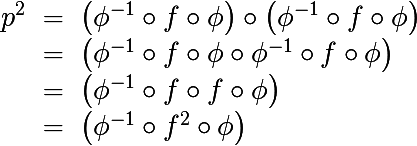
それを示すのは難しくありません

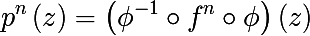
そして、ここで3つの点すべてを組み合わせて、結論を定式化しましょう： 反復の作用下で2次多項式の動作を調査するには、一般的な形式ではなく、ユニタリ中心の形式で調査すれば十分です。これは本当にクールです。なぜなら、一般的には3つの係数があり、単一の中心形式では1つだけだからです。

混oticとした正常な動作

すぐにジュリア集合の定義を与えることが可能になるでしょう。厳密に数学的な定義ではなく、直感的な定義を検討します。しかし、最初に、持続可能性の概念を検討してください。特定の微分方程式の解は、初期に近い条件での解の振る舞いが元の解の振る舞いとあまり変わらない場合、安定と呼ばれます。フレーズ内のすべての塩が非常に異なっていないと推測することは難しくありません 。一般に、さまざまなタイプの安定性が区別されます。たとえば、リアプノフ安定性はジュリア集合の定義に関与します（このより明確な定義は、関数のコンパクトなファミリに関するモンテルの定理から得られます）が、安定性の違いの本質にさえ入らないでしょう。これを説明してみましょう。まず、安定性の直感的な認識を見てみましょう。ここでは、点の青と黄色の軌跡は小さな変化でほぼ同じように動作しますが、赤の軌跡では小さな変化がまったく異なる方向に進みます。

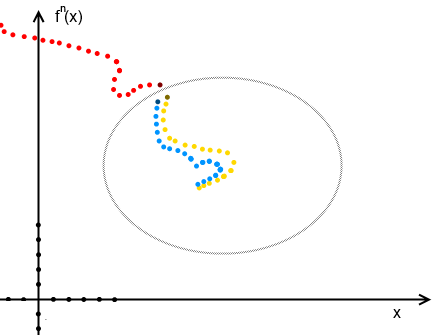
次の多項式f（z）= z ^2-1 + 0.213iを考えて 、 z ₀ = 0.3 + 0.2iおよびz ₀ = 0.31 + 0.2iで100回の繰り返しの軌道を構築しましょう

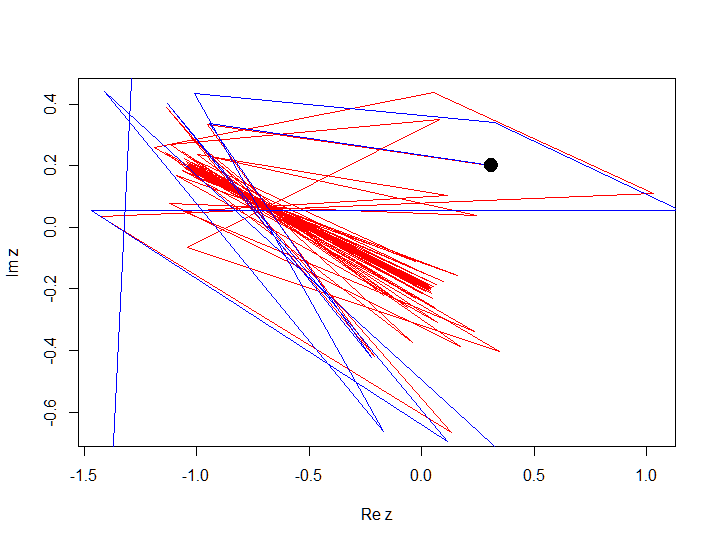
この例では、初期条件の小さな変化が軌道の発散をもたらしたことがわかります。この動作は、開始点の近傍でカオスと呼ばれます。動作は、初期条件の小さな変化に大きく依存しています。安定性が維持される動作、すなわち初期条件の小さな変更は、全体としての動作に大きな影響を与えません。次の例のように、normalと呼びます。次の多項式f（z）= z ^2-1 + 0.2i （定数cをわずかに変更した）を考慮し、 z ₀ = 0.3 + 0.2iおよびz ₀ = 0.31 + 0.2iで100回の反復の軌道を構築します

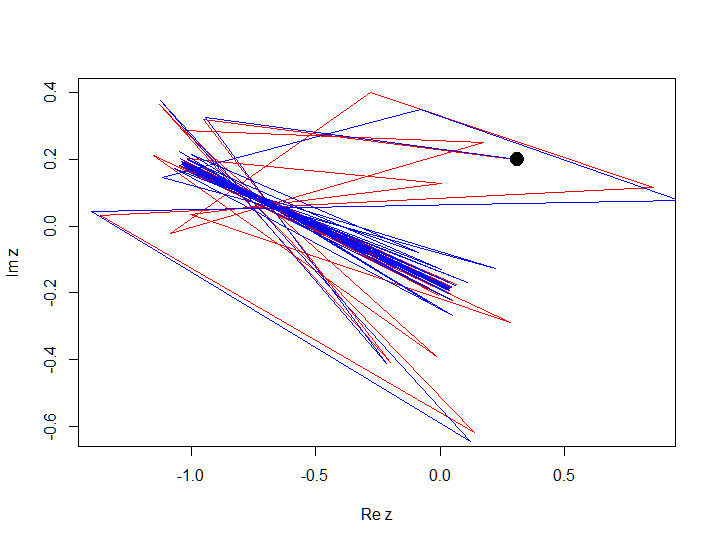
Fatou、Julia、Mandelbrotのセット

多項式f（z）= z ² + c のFatouセットは、反復のアクションの下での関数の動作が通常である各ポイントの複素数セットのサブセットです。初期条件が初期点の小さな近傍で変化しても、反復によって生成される点の軌道はあまり変化しません。 F（f）で示されます。
多項式のジュリア集合 f（z）= z ² + cは、それぞれ、複素数の集合のそのようなサブセットを指します。各点について、反復の作用下での関数の動作はカオスです。開始点のいくつかの小さな近傍での初期条件の小さな変化は、軌跡に大きな影響を与えます。 Jで表示（f）
マンデルブロ集合は、ジュリア集合が接続さ れる多項式f（z）= z ² + cのパラメーターcの集合です。

アトラクタープール

それで、ジュリア集合の意味を学び、そのような集合を構築するためのアルゴリズムに進むことができます。ただし、このためには、まず他の定義をいくつか導入する必要があります。

アトラクタは、時間の経過とともにシステムが発展する方向の動的システムの状態のセットです。この場合、アトラクターは、初期条件に関係なく、関数の反復シーケンスが収束する固定点のサブセットとして理解できます。
関数fの点zの アトラクタプールは、 z （ A（z）で示される）の近傍からの点のサブセットであるため、これらの点のいずれかで開始された軌道はzに収束します
無限大へのアトラクタプールA（∞）とは、軌跡が無限大になる点zのセットを意味します。言い換えれば、それらはある固定点に収束せず、2つ以上の周期点間で振動しません（固定点は周期が1に等しい周期点です）。

多項式f（z）= z ² + cの推論のコンテキストでA（∞）を考えます

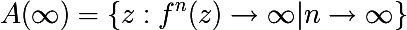
次の定理が存在することがわかります。 （上記のコンテキストの）セットA（∞）は、 open 、 connected、 unboundedです。 Fatouセットに完全に含まれています。 ジュリア集合は、境界 A（∞）と一致します。境界 A（∞）は、すべての複素数の閉じた境界付きサブセットです。

ジュリアセットの構築

二次ダイナミクスのジュリアセットを構築するためのアルゴリズムを作成し、関数ではないことを思い出してください。そのため、 ジュリア集合は境界 A（∞）と一致することがわかりました。境界 A（∞）は、すべての複素数の閉じた境界付きサブセットです。ジュリア集合も閉じられ、境界があります。次のように、関数fの反復によって生成され、制限されたままの複素数のサブセットを示します。このようなセットを、 塗りつぶされたジュリアセットと呼びます。

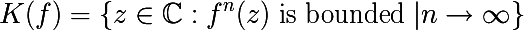
そして、最後に必要な定理は次のとおりです。

f（z）= z ² + cの形式の二次多項式を
示す
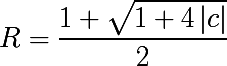
その後、いくつかの点について 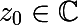n> 0の場合 、次の条件が満たされます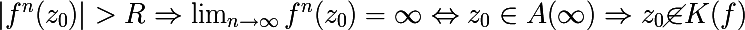
つまり n番目の反復のモジュラスがRより大きい場合、関数fの反復は発散します。これは、アトラクタプールに無限に入る点z ₀に相当します。つまり、 z _0は塗りつぶされたジュリアセットの点で_はありません。

アルゴリズム自体に加えて、この定理から、ジュリア集合全体が原点を中心とする半径Rのボール内にあると結論付けることができます。

PS：ここでは、デザインと黄金のセクション、神秘主義者、オカルトの愛好家について、 f（z）= z ² + 1の場合、しきい値Rは黄金のセクションo_0に等しいことに気付くでしょう

アルゴリズム

cを選択して、多項式f（z）= z ² + cを指定します
与えられた多項式f（z）= z ² + cの Rを計算します
maxIterパラメーターを選択して最大反復数を示します。明らかに高いほど、精度が高くなり、アルゴリズムが遅くなります
色の配列を生成し、maxIter個の合計ピースを作成します。たとえば、明度の低いものから明るいものまで、色で示し、次にポイントがジュリア集合からどれだけ離れているかを示します
各ポイントについて、それが塗りつぶされたジュリアセットの一部であるかどうか、およびしきい値を超えた反復回数を計算します
if | z | > Rは最初の色を使用し、しきい値を超えた反復回数の光を使用します

ジュリア集合生成手順

/// <summary> /// Generate bmp with Julia set /// </summary> /// <param name="c">parameter of square dynamics</param> /// <param name="w">width of bmp</param> /// <param name="h">height of bmp</param> /// <param name="maxIter">max iterations of function</param> /// <param name="xMin">window in complex plane</param> /// <param name="yMin">window in complex plane</param> /// <param name="xMax">window in complex plane</param> /// <param name="yMax">window in complex plane</param> /// <returns></returns> static XBitmap PlotJuliaSet(ComplexNumber c, int w, int h, int maxIter, double xMin = Double.NaN, double yMin = Double.NaN, double xMax = Double.NaN, double yMax = Double.NaN) { double r = CalculateR(c); if (Double.IsNaN(xMin) || Double.IsNaN(xMax) || Double.IsNaN(yMin) || Double.IsNaN(yMax)) { xMin = -r; yMin = -r; xMax = r; yMax = r; } Logger.Instance.Log("R = " + r); double xStep = Math.Abs(xMax - xMin) / w; double yStep = Math.Abs(yMax - yMin) / h; XBitmap bmp = new XBitmap(w, h); IDictionary<int, IDictionary<int, int>> xyIdx = new Dictionary<int, IDictionary<int, int>>(); int maxIdx = 0; for (int i = 0; i < w; i++) { xyIdx.Add(i, new Dictionary<int, int>()); for (int j = 0; j < h; j++) { double x = xMin + i * xStep; double y = yMin + j * yStep; ComplexNumber z = new ComplexNumber(x, y); IList<ComplexNumber> zIter = SqPolyIteration(z, c, maxIter, r); int idx = zIter.Count - 1; if (maxIdx < idx) { maxIdx = idx; } xyIdx[i].Add(j, idx); } } for (int i = 0; i < w; i++) { for (int j = 0; j < h; j++) { int idx = xyIdx[i][j]; double x = xMin + i * xStep; double y = yMin + j * yStep; ComplexNumber z = new ComplexNumber(x, y); bmp.SetPixel(w - i - 1, j, ComplexHeatMap(idx, 0, maxIdx, z, r)); } } return bmp; } private static IList<ComplexNumber> SqPolyIteration(ComplexNumber z0, ComplexNumber c, int n, double r = 0) { IList<ComplexNumber> res = new List<ComplexNumber>(); res.Add(z0); for (int i = 0; i < n; i++) { if (r > 0) { if (res.Last().Mod > r) { break; } } res.Add(res.Last() * res.Last() + c); } return res; } private static double CalculateR(ComplexNumber c) { return (1 + Math.Sqrt(1 + 4*c.Mod))/2; } public static Color ComplexHeatMap(decimal value, decimal min, decimal max, ComplexNumber z, double r) { decimal val = (value - min) / (max - min); return Color.FromArgb( 255, Convert.ToByte(255 * val), Convert.ToByte(255 * (1 - val)), Convert.ToByte(255 * (z.Mod / r > 1 ? 1 : z.Mod / r)) ); }