
「三角測量」のすべての可能なバリエーションをソートするタスクが発生しました。 これらは、単純なルールに従うN個の三角形の「接着」です。
- 三角形はエッジに沿ってのみ接触できます
- 1つのエッジは2つの三角形でのみ共有でき、それ以上は共有できません
たとえば、一意のオプションの3つの三角形のうち、2つしか存在できません。
[[ABC]、[ABD]、[ACD]]
[[ABC]、[ABD]、[ACE]]
接着オプションの総数は120であるという事実にもかかわらず、検索プロセスを適切に最適化できたため、N = 11までのほとんどすべてのオプションを計算できましたが、これはまだ非常に小さいです。
私はそれをどのように最適化したかをお話しします。おそらく、尊敬されている人々がこのプロセスをスピードアップする方法についてのアイデアを持っているでしょう。
素朴なアプローチ
N = 3のオプションを考えます。3つの三角形、9つの頂点。 頂点に0〜8の番号を付け、000 000 000から888 888 888までのすべてを繰り返します。
ご覧のとおり、これは3つの三角形であっても非常によく似ています。 さて、ここで絶えず遭遇する三角形の繰り返しは、ここでは何も必要ありません。
組み合わせアプローチ
長い夜の思考により、頭は次の思考を生むことができました。
すべての三角形は少なくとも1つのエッジで接着する必要があるため、N個の三角形からの接着に必要な頂点の最大数はN * 3未満でなければなりません。
実際、最長の有効な接着は次のようになります。
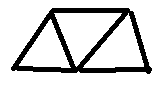
また、9個ではなく5個の一意の頂点しか存在しないことは明らかです。一般的な場合、 一意の頂点の数は、式N + 2によって得られます。ここで、Nは三角形の数です。 さらにユニークな頂点がある場合、三角形の1つは必然的に1つの頂点のみで他の三角形に接続しますが、これは間違っています。
だから。 3つの三角形の5つの一意の頂点。
合計の組み合わせは(組み合わせ論と二項係数を思い出してください)5! /(3!(5-3)!)= 10
これは、頂点のすべての組み合わせを生成することで取得できる一意の三角形の数です。
さて、今、3つの三角形の組み合わせに対して同じ二項係数を考えます
10! /(3!(10-3)!)= 120 。 これは、すべてのオプションを考慮するために通過する接着剤の数です。
一般的に、組み合わせの数の式は次のとおりです。

階乗がいくつありますか? たとえば、N = 10の場合、合計で59,473,554,359,599,446の組み合わせがあります。これは、並列化されていてもたくさんあります。
小さなN(3,4,5 ..)で検索を開始したとき、プログラムはすべての組み合わせをすばやく見つけ、残りはただの重複であることに気付きました(同型のグラフをチェックするVF2アルゴリズムによって削除されます)
非常に高速-これは、たとえばN = 5の最後の「良好な」接着が324,632のうち2084ステップで検出されたことを意味します。これは全範囲の0.642%です。 N = 6の場合、これは0.3644%です。 N = 8で最後に計算したのは0.1352%でした。
つまり、N + 1の一般的なケースでは、以前の範囲の何パーセントが計算されたかを調べ、同じ数を数えます。これにより、すべてがチェックされることが保証されます。 確かに、N = 9の場合、これはまだ少しです(0.1352%をチェックすると、270 485 377 680)
ですから、何か他のものを考え出す必要がありました。
反復アプローチ
もう少し長い夜と別のアイデア:
しかし、すべての可能な組み合わせで1つの三角形を追加して、Nのすべての接着剤に基づいてN + 1のすべての接着剤を生成するとどうなりますか?
つまり、トリプルには2つしかないことを知っています。
[[ABC]、[ABD]、[ACD]]
[[ABC]、[ABD]、[ACE]]
そして、4は6です
[[ABC]、[ABD]、[ACD]、[BCD]]
[[ABC]、[ABD]、[ACD]、[BCE]]
[[ABC]、[ABD]、[ACE]、[ADE]]
[[ABC]、[ABD]、[ACE]、[ADF]]
[[ABC]、[ABD]、[ACE]、[BCF]]
[[ABC]、[ABD]、[ACE]、[BDF]]
4つすべてが前のトリプルから来ていることがわかります(順列は辞書式順序で生成されます)
すべてうまくいきますが、さらに自分自身を生成しますが、 ! このアプローチを確認したところ、たとえば5がすべてこのように生成されるわけではないことがわかりました。
[[ABC]、[ABD]、[ACD]、[BCE]、[BDE]]
[[ABC]、[ABD]、[ACD]、[BCE]、[BDF]]
[[ABC]、[ABD]、[ACD]、[BCE]、[BEF]]
[[ABC]、[ABD]、[ACE]、[ADE]、[BCF]]
[[ABC]、[ABD]、[ACE]、[ADF]、[AEF]]
[[ABC]、[ABD]、[ACE]、[ADF]、[AEG]]
[[ABC]、[ABD]、[ACE]、[ADF]、[BCG]]
[[ABC]、[ABD]、[ACE]、[ADF]、[CEG]]
[[ABC]、[ABD]、[ACE]、[BDE]、[CDE]]
[[ABC]、[ABD]、[ACE]、[BDF]、[CEG]]
よく見ると、最後から2番目の5つは、4つすべてと1つではなく2つの三角形で異なっていることがわかりました。 トポロジの観点では、これは「Mobius strip」です。 また、三角形を1つも使わずに描画しようとすると、三角形のグループが1つの頂点のみに接触する状況になりますが、これは完全に悪いことです。
とにかく、抜け道はあります。 Nの結果の組み合わせをすべて取り、最後から1つの三角形を微調整し、他の2つのオプションをすべて「生成」してチェックします。 とにかく、組み合わせ検索よりも何倍も高速です。
しかし、いいえ、N = 8で、2つではなく3つの三角形だけで7つすべてと異なる三角形分割がありました。
したがって、N = 9から開始して、2つの三角形が引き抜かれ、3つの三角形が「生成」されます。 これにより、N = 11および12の始まりまでのほとんどすべてのオプションを計算することが可能になりました(ほとんど-おそらく3つ以上の三角形の接着剤が存在するため)。 このすべてを並列化したという事実にもかかわらず。 私のための1つのスレッドは接着の最初のチェックを実行し、残りの3つは重複のカットに従事しています 同型のグラフをチェックすることは、かなりリソースを消費するタスクです。
一般に、すべてのオプションが必要ない場合は、ピンチオフ(またはピンチオフ)して残りのオプションを再生成できますが、これは確かに悪いことですが、この方法では、大きなNでもいくつかのオプションが確実に提供されます。 »有効な接着剤のセット全体を取得します。
しかし、全体が面白いです!
グラフの列挙のトピックに関する資料をすでに検索しましたが、急勾配の反復法には考えがありませんでした。 たぶん、あなたはこの主題について考えているでしょうか?
たとえば、三角形の組み合わせが生成されると、最初の三角形は常に次のようになります。
ABC ABD ABE ABF ABG ...
ABが2回以上繰り返されていることがわかります。 そのようなケースが最初に存在しないバリアントを生成できれば、組み合わせバリアントのアイデアはより単純になりますが、そのようなシーケンスを生成する方法はわかりません。
PSそれは表面の分類に関する科学的研究に必要です。 もちろん、N = 11までのデータを提供しても問題はありません(そのようなデータもありません(たとえば、トーラスは14個の三角形から構築できますが、もう1年間計算する必要があります)。 しかし、Nを押しのける方法を考え出すのは興味深いでしょう。 ご清聴ありがとうございました。
UPD
より早く終了する必要がありましたが、今だけです。 Nからの接着から三角形のペアを分割すると、N + 1の検索を開始する前に削除できる一連の明示的な重複が得られます。 良いスピードブーストが判明