⏩ 🙏🏻 👨🏿‍🎤 DESからJへの100行 👩🏾‍🤝‍👨🏽 🤲🏼 🈯️

JSでの30週間は、本当に異常なもので薄められるべきです。

たとえば、この一連の記事や本を読む前に読むことをお勧めします。ここの言語辞書; それにもかかわらず、私は自分の行動を詳細に説明しようとします（記事を煩雑にしないために、すべての説明はネタバレの下に隠されています）。

コードについて質問、提案、修正がある場合は、コメントを歓迎します。

DESとは

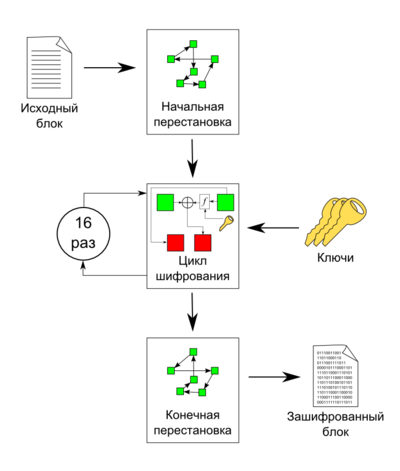
DES （データ暗号化標準）は、IBMによって開発され、1977年に米国政府によって公式標準（FIPS 46-3）として承認された対称暗号化アルゴリズムです。

DESは、56ビットキーを使用する一般的なブロック暗号です。暗号化プロセスは、64ビットブロックのビットの初期順列、16サイクルの暗号化、および最後にビットの逆順列で構成されます。

地面の準備

DESは、事前に準備する価値があるいくつかのマトリックスを使用します。

初期置換行列P

パターンは肉眼で見ることができます。上から下へ右から左へのマトリックスの上半分には1から63までの奇数があり、マトリックスの下半分の各要素は対応する上要素の要素よりも1つ小さくなっています。これを活用してください。

解説

まず、トップを作ります。

|: |. 8 4 $ >: +: i.32 57 49 41 33 25 17 9 1 59 51 43 35 27 19 11 3 61 53 45 37 29 21 13 5 63 55 47 39 31 23 15 7

コードは右から左に実行されます。順番に：

i.32

は、ゼロから始まる32個の連続した数値を生成します。
+:

オペランドを2倍にします。
>:

オペランドを1つ増やします。
8 4 $

は、オペランドを8x4行列に変換します。
|.

マトリックスの主軸を反転します。文字列を逆順に並べ替えます。
|:

行列を転置します。

順次

  i.32 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 +: i.32 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62 >: +: i.32 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 8 4 $ >: +: i.32 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 |. 8 4 $ >: +: i.32 57 59 61 63 49 51 53 55 41 43 45 47 33 35 37 39 25 27 29 31 17 19 21 23 9 11 13 15 1 3 5 7 |: |. 8 4 $ >: +: i.32 57 49 41 33 25 17 9 1 59 51 43 35 27 19 11 3 61 53 45 37 29 21 13 5 63 55 47 39 31 23 15 7

マトリックスの下半分を取得するのに費用はかかりません。

  <: |: |. 8 4 $ >: +: i.32 56 48 40 32 24 16 8 0 58 50 42 34 26 18 10 2 60 52 44 36 28 20 12 4 62 54 46 38 30 22 14 6

<:

演算子は、オペランドの値を1つ減らします。

これを結合することは残っています-ここでJの魔法が作用します：

  (] , <:) |: |. 8 4 $ >: +: i.32 57 49 41 33 25 17 9 1 59 51 43 35 27 19 11 3 61 53 45 37 29 21 13 5 63 55 47 39 31 23 15 7 56 48 40 32 24 16 8 0 58 50 42 34 26 18 10 2 60 52 44 36 28 20 12 4 62 54 46 38 30 22 14 6

3動詞構成はforkと呼ばれます。

(fgh) y <-> (fy) g (hy)

したがって、上記の構成はこれと同等です。

 (] |: |. 8 4 $ >: +: i.32) , (<: |: |. 8 4 $ >: +: i.32)

ダイアドは配列の連結を実行し、 ]

は正しいオペランドを返します。

モナドのバリアント,

、行列を配列,

「直線化」し、これを使用して、初期順列の行列の最終式を取得します。

 P =: , (] , <:) |: |. 8 4 $ >: +: i.32

逆置換行列P ^-1

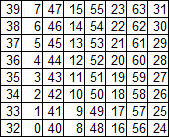
この行列は次のようにPに対応します。P ^-1の 0番目の要素は39、Pの39番目の要素は0などです。

つまり、行列P ^-1の要素は、行列Pのインデックスのインデックスです。紛らわしいように聞こえますが、これはこの行列の式の根底にあります。

説明

最初のステップは、ダイアドフォークを使用することです。

x (fgh) y <-> (xfy) g (xhy)

 (i.64) ([ * =/~) P

結果は64x64マトリックスで、各行には位置P [i]の番号（たとえばi）が含まれ、残りの要素にはゼロが埋め込まれます。

forkに加えて、副詞/

と~

が使用されます。1番目は、動詞を配列の各要素に適用し、2番目はオペランドを交換します。

xf~ y <-> yfx

u

が二項動詞であるu/ y

を書くと、Jはyのすべての要素の間でそれを置き換えます。

+/ 1 2 3 <-> 1 + 2 + 3

または、行を追加して最終的な式を取得することにより、マトリックスに適用します。

 iP =: +/ (i.64) ([ * =/~) P

鍵Gの初期順列の行列

7番目、15番目などのビットはキーから「破棄」され、パリティを制御します。

Gのパターンはそれほど明白ではありませんが、連続した数字の8x8マトリックスからマトリックスGを取得することは難しくありません。そこから最後の列が単純に捨てられました。

説明

  }: |: i. 8 8 0 8 16 24 32 40 48 56 1 9 17 25 33 41 49 57 2 10 18 26 34 42 50 58 3 11 19 27 35 43 51 59 4 12 20 28 36 44 52 60 5 13 21 29 37 45 53 61 6 14 22 30 38 46 54 62

i. 8 8

数字の配列の代わりにi. 8 8

使用すると、連続した数字の8x8マトリックスが直ちに作成されます。
}:

配列の最後の要素/行列の行をスローします。

転置はむしろ副作用ですが、マトリックスが必要なのはこの形式です。

次に、結果を適用する場合にのみ、行を反転する必要があります|.

、その後、行全体が交換されます。この場合、個々の行で機能するように動詞のランクを変更する必要があります。

  |."1 }: |: i. 8 8 56 48 40 32 24 16 8 0 57 49 41 33 25 17 9 1 58 50 42 34 26 18 10 2 59 51 43 35 27 19 11 3 60 52 44 36 28 20 12 4 61 53 45 37 29 21 13 5 62 54 46 38 30 22 14 6

"

は、動詞のランクを変更します。ランク0は、動詞がオペランドの各要素に適用され、1が行に、2がマトリックス全体に適用されることを意味します。

結果を変数G

保存します-これはより便利です。

マトリックスの最初の28個の要素が必要なとおりであることは既に明らかです。別の24個は行の順序を逆にすることで取得できます。残りの4つの要素を適切に引き出すことに成功しなかったので、そのまま入力します。

  4 14 $ (28 {. , G), (24 {. , |. G), (27 19 11 3) 56 48 40 32 24 16 8 0 57 49 41 33 25 17 9 1 58 50 42 34 26 18 10 2 59 51 43 35 62 54 46 38 30 22 14 6 61 53 45 37 29 21 13 5 60 52 44 36 28 20 12 4 27 19 11 3

N {. y

N {. y

はN {. y

から最初のN

要素を引き出します。

結果を保存します。

 G =: |."1 }: |: i. 8 8 G =: (28 {. , G), (24 {. , |. G), (27 19 11 3)

KPキー置換行列

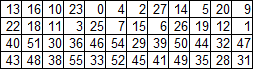
ここではすべてが悲しい-パターンは見えないので、マトリックスをそのまま書きます。

Sシフト行列

最初の行はインデックス、2番目の行は値です。ここでは詳しく説明しません。

 s =:1, (14 $ 1, 6 $ 2), 1

拡張行列E

この行列はi. 8 4

から簡単に取得できi. 8 4

i. 8 4

：左の列は周期的に下にシフトされて右側のマトリックスに配置され、右の列は上にシフトされて左側に配置されます。

 E =: |: i. 8 4 E =: , |: (_1 |. _1 { E) , E , (1 |. 0 { E)

演算子x |. y

x |. y

は、配列の循環シフトを実行します。

P2順列行列_{（はい、DESには多くの順列があります）}

ここでも、パターンは表示されません。さらに進みましょう。

S変換行列

それは巨大で、三次元的であり、規則性もまったく見られません。

このマトリックスをそのまま書き留めると同時に、後で対処しやすいように、いくつかの動詞を作成します。

 f =: dyad : '|. #: S {~ < x, ((5{y)++:0{y), (+/(2^i.4)*}:}.y)' " 0 1 fS =: monad : '}. |."1 (4 $ 1), (i.8) f 8 6 $, y' " 2

説明

2番目の動詞から始めましょう。これはランク2のモナドで、マトリックスを8x6形式に変換し、右オペランドを最初の動詞に送ります。左のオペランドはi.8

です。次に、4つのユニットの行が結果に追加され、マトリックスのすべての行が反転され、最初の行が削除されます。

最初の動詞はランク0 1のダイアドです（ダイアド動詞のこのようなランクは、ランク0が左オペランドに適用され、1が右オペランドに適用されることを意味します）。この動詞は、右側のオペランドが長さ6のビットの配列であると見なします。0番目と5番目のビットはSの行番号を決定し、ビット1〜4は列番号を決定し、左側のオペランドはサブマトリックスの番号を決定します。受信した3つの数値はすべて、ボックス（構造体のローカルアナログ）に詰め込まれ、入力演算子{

-インデックスから配列から取得します。演算子#:

結果を2進数に変換します。これは次のステップで反転されます。

結果ラインに先行ゼロを追加するには、4つのユニットの行を追加および削除するこのすべての叙事詩が必要です。最初に反転しない場合、最後にゼロが追加されます。

ビジネスに取り掛かろう

最初に、使用するキーのリストを作成します（ key

既に定義されていると信じていkey

）。

説明

最初に、文字を自己記述モナドによってバイナリ表現に変換し（記事にはコードはありません）、キーGの初期順列の行列を結果に適用します。

 binkey =. chr2bin key prmkey =. G { binkey

次に、結果の最初の28ビットを取得し、シフトの結果のリストを作成します。

 C =. (28 {. prmkey) |.~"1 0 +/\s

この行の新機能のうち、副詞\

のみ：各オペランド接頭辞に動詞を適用します。

  s 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1 +/\s 1 2 4 6 8 10 12 14 15 17 19 21 23 25 27 28

最後の28ビットについても同じことを行います。

 D =. (28 }. prmkey) |.~"1 0 +/\s

N }. y

N }. y

は、 N }. y

の最初のN

要素を破棄します。

次に、対応する行を連結し、KPキー置換行列を結果の各行に適用する必要があります。

 K =. KP {"1 C ," 1 1 D

 binkey =. chr2bin key prmkey =. G { binkey C =. (28 {. prmkey) |.~"1 0 +/\s D =. (28 }. prmkey) |.~"1 0 +/\s K =. KP {"1 C ," 1 1 D

元の8バイトのテキストは、2つの32ビット部分に分割されます。

 bin =. chr2bin plain prm =. P { bin L =. 32 {. prm R =. 32 }. prm

次のように、各キーをペアL、Rに適用する必要があります。

これを行うには、3つの値を持つボックスを受け取り、同様のボックスを返す再帰モナドを作成します。

説明

>

ボックスを「開き」、その内容を返します。

 K =. > 0 { y L =. > 1 { y R =. > 2 { y

上の画像のf関数は次のことを行います。

展開行列EをRに適用します。
2を法とするキーで結果を追加します。
結果の6ビットブロックごとに、行列S内の対応する4ビット数を見つけます。
これに置換行列P2を適用します。
2を法とするLの結果を追加します。

パラグラフ3には特別な動詞があります。上記はすべて簡単な行で説明されています。

 L ~: P2 { , fS (0 { K) ~: E { R

 step =: monad define K =. > 0 { y L =. > 1 { y R =. > 2 { y (}. K); R ; L ~: P2 { , fS (0 { K) ~: E { R )

そして、キーがある限り何度でも呼び出します。

 result =. step^:(#K) K; L; R

説明

この行の新しいもののうち、ユニオンu^:N

のみです。これは動詞u Nを実行します。たとえば、

u^:4 y <-> uuuuy

繰り返しますが、LとRを交換して暗号化されたテキストを取得します。

 R =. > 1 { result L =. > 2 { result bin2chr iP { ,L,R

左のオペランドを持つキーと右の8バイト配列を受け入れるダイアドにすべてをラップしてみましょう。

ここに長いダイアド

 encode =: dyad define key =. x binkey =. chr2bin key prmkey =. G { binkey C =. (28 {. prmkey) |.~"1 0 +/\s D =. (28 }. prmkey) |.~"1 0 +/\s K =. KP {"1 C ," 1 1 D plain =. y bin =. chr2bin plain prm =. P { bin L =. 32 {. prm R =. 32 }. prm result =. step^:(#K) K; L; R R =. > 1 { result L =. > 2 { result bin2chr iP { ,L,R )

復号化はまったく同じ方法で実行されますが、唯一の違いはキーが逆の順序で使用されることです。

持っているものを適用する前に、テキストを準備する必要があります。

in.txt：

Lorem ipsum dolor sit amet consectetur adipiscing elit.

説明

1!:1

はファイルの内容を読み取ります

 plaintext =: 1!:1 < 'in.txt'

アルゴリズムはそれぞれ8文字のブロックで機能するため、スペースを空けてテールを打つ方が適切です。そうしないと、テキストが単純に繰り返されます。

 ' ',~^:(8 - 8| # plaintext) plaintext

次に、テキストを8文字のブロックに分割します。

 plaintext =: (8,~ >. 8 %~ #plaintext) $, ' ',~^:(8 - 8| # plaintext) plaintext

 plaintext =: 1!:1 < 'in.txt' plaintext =: (8,~ >. 8 %~ #plaintext) $, ' ',~^:(8 - 8| # plaintext) plaintext

結果をファイルに書き込みます。

説明

1!:21

はファイルを開き、 1!:22

閉じ、 1!:2

はファイルに書き込みます

 out =: 1!:21 < 'out.txt' ('habrhabr' encode"1 1 plaintext) 1!:2 out 1!:22 out

out.txt：

4acc c8ad 32dd 96a1 ae9c 2fdc 2025 e3d0 968c 97c0 5544 0944 2d20 2069 f943 f0d4 e98d bdea 71f9 c516 8a0a b034 5641 b0b5 53cc 2355 2fb1 4bde

そして、結果を解読してみてください。

  cipher =: 1!:1 < 'out.txt' cipher =: (8,~ >. 8 %~ #cipher) $, cipher , 'habrhabr' decode"1 1 cipher Lorem ipsum dolor sit amet consectetur adipiscing elit.

コードはすべてpeystbinにあります。

コードについて質問、提案、修正がある場合は、コメントを歓迎します。

ご清聴ありがとうございました！

DESからJへの100行