それはすべて、正八角形と八角形の特性を研究したいという願いから始まりましたが、結果はすべての凸多角形(多角形)とそれらに組み込まれた星に適用できることが判明しました(類推により、私はそれらをポリグラムと呼びます-五penta星、六gram星、七、星、八etc星など-これはこの用語には他の意味があります)。
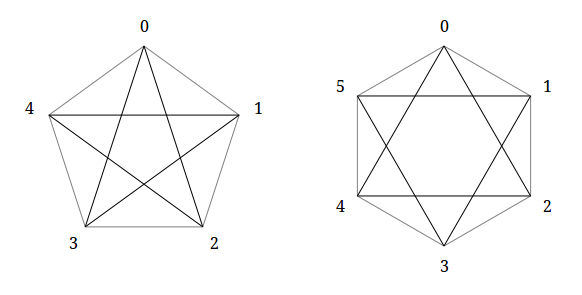
はじめに、用語。 五角形は五角形のすべての対角線のセットです;六角形の場合、これはすべての対角線ではなく、六角形の反対の頂点を接続するものだけです。 どちらの場合も、これらのピークは次々と通過します。 たとえば、五角形の頂点の番号が
定義は、1〜n / 2の値の範囲を持つ整数kとして「ポリグラム次数」の概念を導入することで要約できます。ここで、nは元のポリゴンの角度の数です。 上限k(整数部分
五角形の場合、式によると、2つの一般化された五gram星があります-五角形自体と古典的な意味での五gram星。

ヘクスの場合、3つの一般化されたヘキサグラムがあります:ヘックス自体、古典的なヘキサグラム、および反対側の頂点を接続する対角線(縮退ケース)。

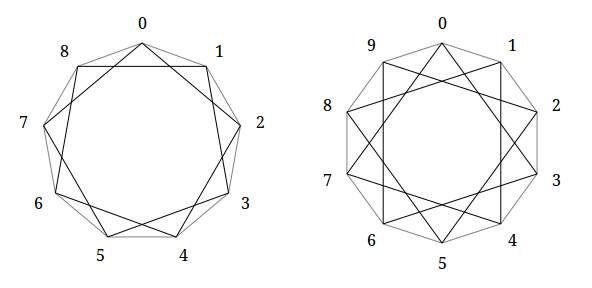
わかりやすくするために、9角形と8角形のポリグラムを分析します。 式によれば、セプタグラムの数は3、オクタグラムの数は4です。

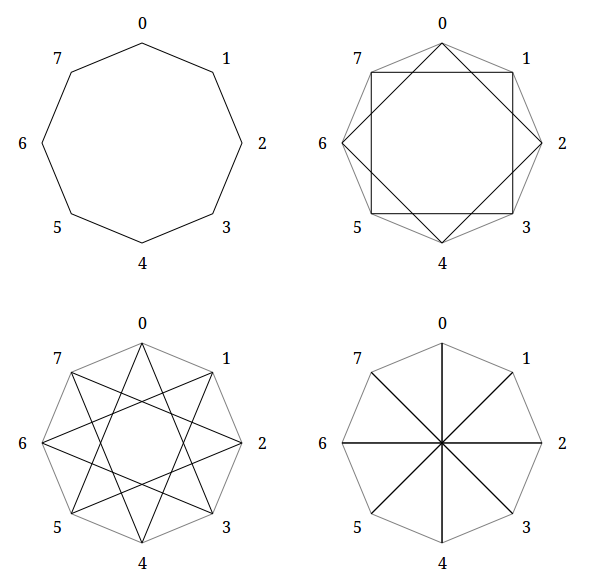
副作用として、ポリグラムは自然に接続と切断に分割されることがわかります。 接続されたポリグラムは、エッジに沿ってパスがある頂点のペア間のポリグラムです(ポリゴンの頂点でのみエッジからエッジにジャンプできます)。 数値の理論を使用すると、元のポリゴンの角の数とポリグラムの順序が互いに素である場合にのみ、ポリグラムが接続されていることに気付くことができます。
以下の図は、切断されたポリグラムの例を示しています。個々の部分は異なる色で強調表示されています。 ノグラム

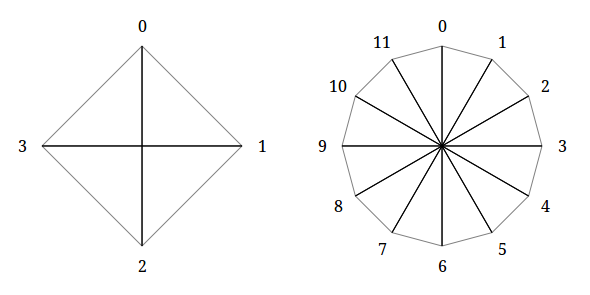
これで、同じ数の角度(
さらに、そのような場合の偶数および最大の場合、k(k = n / 2)ポリゴンは、反対の頂点を結ぶ対角線のセットに縮退します。
私にとってはまったく予想外でしたが、結果は、ポリグラムの頂点の角度の合計(凸多角形の場合)がかなり単純な計算可能な量であるということでした:
上記のすべての図と推論は、凸面ポリゴン上に構築されたポリグラムに適用されます。 図では、私自身の怠lazだけから正しいポリグラムの例を描いた-描画プログラムを書く方が簡単だった。 さらに、正しいポリグラムのみに焦点を当てます。
上記の式に基づいて、通常のポリグラムの頂点の角度は
正しいポリグラムの地平線(外部ポイントのセット)を取得すると、この図は非凸2n-gon(nはポリグラムの頂点の数です。右側の図の境界線はこれを示しています。

したがって、追加の「余分な」角度がn個あり、これをポリグラムの内部コーナーと呼びます。 これらの角度は非凸であり、通常のポリグラムのポリゴン角度の合計から、それらは
これらの計算は、パターンと面白い装飾を構築するのに役立ちます。これについては、以下で患者の読者に説明します。
次はかなり役に立たない部分です。これは一度に美的な喜びを与えてくれましたが、その結果は読者の失われた時間にしかならず、それが「面白いタスク」をハブに追加する理由でした。
オクタグラムパターン k = 2の 場合、光線間の 角度はπ-2π/ n になります。これは、ポリグラムが作成される元のポリゴンの角度とまったく同じです。 どのような場合、そのようなポリゴンは互いに密接に隣接し、一種のモザイクを形成しますか? つまり、ポリグラムの上部の角度とポリゴンの上部の2倍の角度の合計は2πである必要があります。 この場合の通常のポリグラムの頂点の角度はπ-4π/ n です。 したがって、方程式が得られます。
π-4π/ n + 2(π-2π/ n)=2π
3π-8π/ n =2π
8π/ n = pi;
n = 8
したがって、k = 2のオクタグラムは、8つの八角形を描画することで取得できます。隣接する辺には共通の側面があります。

オクタグラム(n = 8、k = 2) は切断され、2つの正方形で構成されています(すべての頂点の角度は直線です: π-4π/ 8 =π/ 2 )。 このようなオクタグラムの光線では、辺がビームの辺に等しい正方形を構築できます。
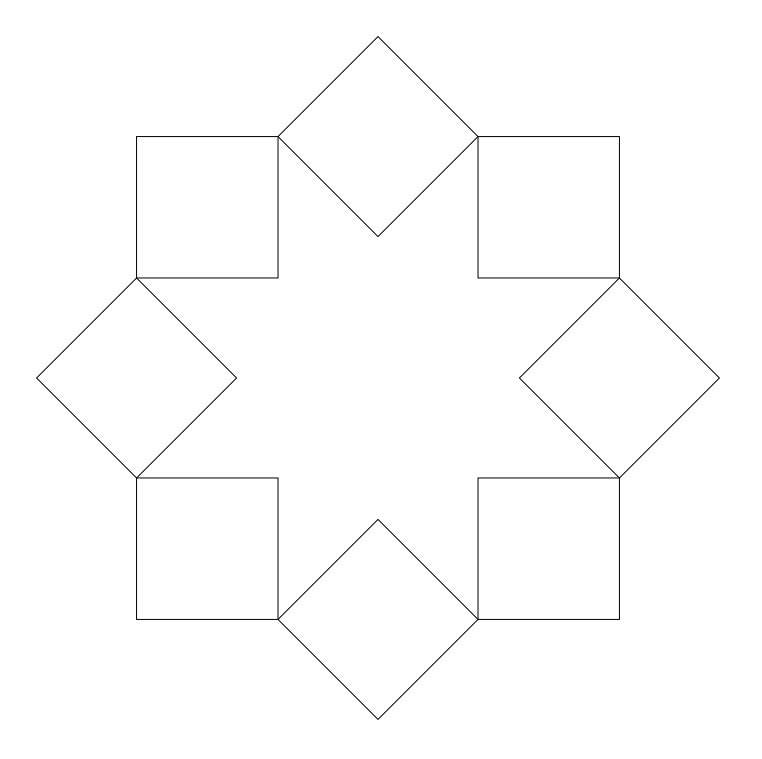
このオクタグラムの内側の角は5π/ 4 です。 光線上に構築された正方形の角度の合計を内部角度から減算すると、オクトグラム内の隣接する正方形の辺間の角度が得られます。 この角度はπ/ 4 です。 したがって、正方形の内側は、8つの頂点π/ 4の 角度と光線π/ 2の 角度(正方形の頂点の角度)を持つ星型の図形を形成します。 したがって、この図の内角は3π/ 2になり ます。
オクタグラムの角度(n = 8、k = 3)を 考慮すると、頂点の角度はπ-2πk/ n =π/ 4 であり、内角はπ+2π(k-1)/ n =3π/ 2 であることがわかります。これは、上記の正方形で囲まれた図と正確に一致します。
これらの計算の実例は素晴らしい絵です:
したがって、k = 2のオクタグラムは、8つの八角形を描画することで取得できます。隣接する辺には共通の側面があります。

オクタグラム

このオクタグラムの内側の角は
オクタグラムの角度
これらの計算の実例は素晴らしい絵です:

六角形の六角形のモザイク
再びk = 2 の場合を考えます。 オクタグラムの場合で上述したように、この場合、ポリグラムの頂点の数に等しい角度の数を持つ正多角形は、正多角形の光線間の角度に内接することができます。 この場合、2つのポリゴンの角度とそれらが隣接するポリグラムの光線の合計は、 n> 8の 場合は2πを超え、 n <8の 場合は2π未満になります。 最初のケースでは、現時点で興味深い何かを構築することは成功せず、2番目のケースでは、残りの場所に別の何かを入力できます。 これは、別のポリゴンまたはポリグラムのレイにすることができます。
これが3番目のポリゴンの場合、辺の数は次の方程式で計算できます。
π-4π/ n + 3(π-2π/ n)=2π
2π-10π/ n = 0
n = 5
したがって、五角形の星の光線の周りに、五角形の上部に共通の頂点を持つ3つの五角形を描くことができます。 残念ながら、この場合、モザイクは機能しません。ただし、上記と同様のパターンを除き、3つの五角形が各光線の上部にグループ化されます。

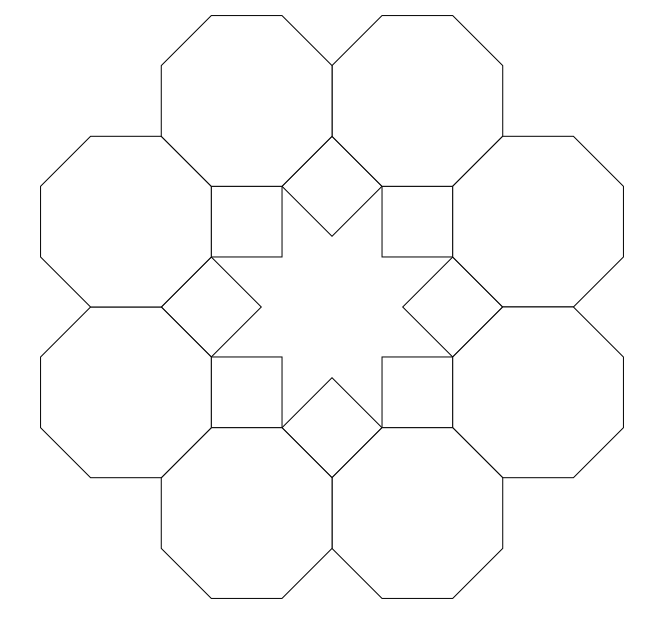
2つのポリゴンと2つの光線の場合を考えると、次の方程式に到達できます。
2(π-4π/ n)+ 2(π-2π/ n)=2π
2π-12π/ n = 0
n = 6
結果はこのモザイクです:

これが3番目のポリゴンの場合、辺の数は次の方程式で計算できます。
したがって、五角形の星の光線の周りに、五角形の上部に共通の頂点を持つ3つの五角形を描くことができます。 残念ながら、この場合、モザイクは機能しません。ただし、上記と同様のパターンを除き、3つの五角形が各光線の上部にグループ化されます。

2つのポリゴンと2つの光線の場合を考えると、次の方程式に到達できます。
結果はこのモザイクです:
