まえがき
すべての良い一日。 新しい、あまり知られていないヒューリスティックな最適化方法の一連の記事から、次の記事に注目してください。 本日の投稿は、Esmat Rashedi、Isaac Newton、および重力によるものです。
歴史的背景
重力検索（GS）は非常に新しいアルゴリズムです。 2009年に登場し、中心力法の論理的な発展でした。 GSは、重力と質量相互作用の法則に基づいています。 原則として、このアルゴリズムはマルチエージェントシステムの開発に基づいているため、Particle Swarm Optimization（PSO）に似ています。
戦略
GSは2つの法律で動作します。
- 重力：各粒子は他の粒子を引き付け、2つの粒子間の引力はそれらの質量の積に直接比例し、それらの間の距離に反比例します（重力の普遍的な法則とは異なり、距離の2乗は使用されないことに注意する必要があります。最良の結果が得られるかどうかをテストし、良心に任せてください）
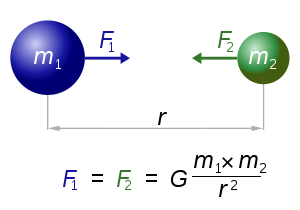
- 移動：粒子の現在の速度は、前の瞬間の速度の一部と速度の変化の合計に等しく、これはシステムが粒子に作用する力を粒子の慣性質量で除算した力に等しい。
武器庫にこれらの2つの法則があるため、この方法は次の計画に従って機能します。
- システムをランダムに生成する
- 各粒子の適合度の決定、
- 重力定数、最良および最悪の粒子、ならびに質量の値を更新し、
- さまざまな方向に生じる力の計算、
- 加速度と速度を数え、
- 粒子位置の更新、
- 完了基準が満たされるまでステップ2〜6を繰り返します（最大反復数を超えるか、位置の変更が少なすぎるか
、魂が他の意味のある基準を必要とする）。
アルゴリズムのより詳細な説明に興味がある人向け
したがって、最小化する必要がある関数がいくつかあります。 
。 また、エリアがあります 
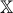粒子の初期位置が生成されます。 GSの作業計画によると、すべてはパーティクルシステムの生成から始まります 
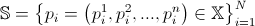どこで 
-システム内のパーティクルの最大数。
時間に作用する力
に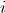 
横からの粒子 
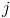th、式により計算 
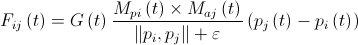どこで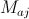 
-アクティブな重力質量 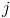番目の粒子 
-受動的な重力質量 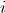番目の粒子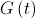 
-対応する瞬間の重力定数、 
小さな定数です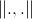 
-粒子間のユークリッド距離。
その結果、アルゴリズムは決定論的ではなく、結果の力を計算するための式で確率論的です
ランダムな値が追加されます 
（ゼロから1に均等に分散）。 そして、結果の力は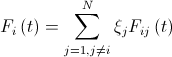 
。
加速度と速度を計算します。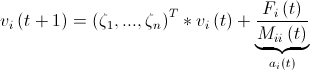
どこで 
-ベクトルの成分ごとの乗算の操作、 
-ゼロから1まで均一に分布するランダム変数、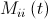 
-不活性質量 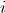番目の粒子。
粒子の位置を数えるために残っています。 とても簡単です：
。
現時点では、重力定数がどのように変化するのか、粒子の質量をどのように計算するのかという2つの疑問が残ります。 重力定数の値は、定数の初期値に応じて、単調に減少する関数によって決定される必要があります
そしてポイントインタイム 、つまり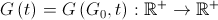 
。
たとえば、次の機能を使用できます。
これで、物語の最後の部分である、大衆を詳しく説明することができます。 最も単純なケースでは、3つの質量（受動、能動、慣性）がすべて同一視されます。
。 次に、式に従って質量値を計算できます。 
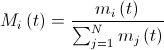どこで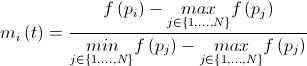 
。
もちろん、物理的な重要性に基づいて質量を計算することはできますが、それにもかかわらず、ラシェディはこれを言っていません（私が見つけることができる著者は誰もいません）。
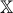。 また、エリアがあります 粒子の初期位置が生成されます。 GSの作業計画によると、すべてはパーティクルシステムの生成から始まります 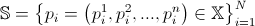どこで -システム内のパーティクルの最大数。
時間に作用する力
に 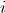横からの粒子 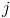th、式により計算 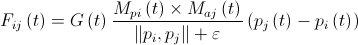どこで 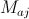-アクティブな重力質量 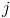番目の粒子 -受動的な重力質量 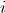番目の粒子 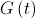-対応する瞬間の重力定数、 小さな定数です 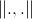-粒子間のユークリッド距離。
その結果、アルゴリズムは決定論的ではなく、結果の力を計算するための式で確率論的です
ランダムな値が追加されます （ゼロから1に均等に分散）。 そして、結果の力は 。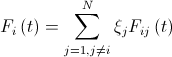
加速度と速度を計算します。
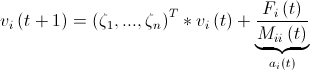どこで -ベクトルの成分ごとの乗算の操作、 -ゼロから1まで均一に分布するランダム変数、 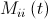-不活性質量 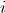番目の粒子。
粒子の位置を数えるために残っています。 とても簡単です：
。
現時点では、重力定数がどのように変化するのか、粒子の質量をどのように計算するのかという2つの疑問が残ります。 重力定数の値は、定数の初期値に応じて、単調に減少する関数によって決定される必要があります
そしてポイントインタイム 、つまり 。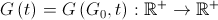
たとえば、次の機能を使用できます。
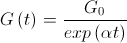どこで 
： 
、 
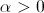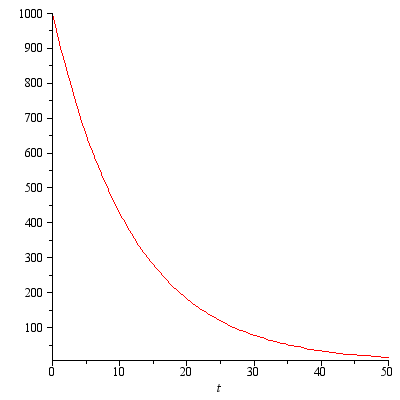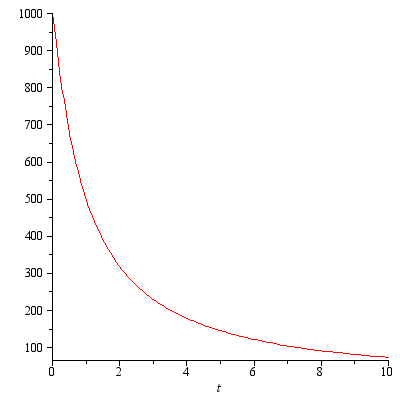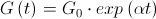どこで 
： 
、 
どこで 
： 
。
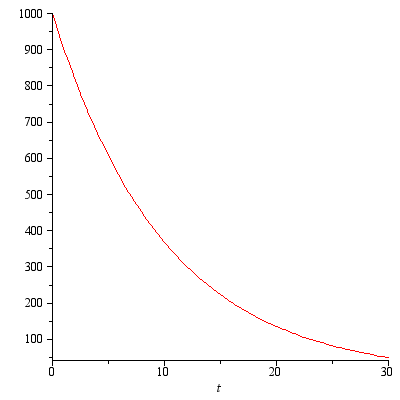これで、物語の最後の部分である、大衆を詳しく説明することができます。 最も単純なケースでは、3つの質量（受動、能動、慣性）がすべて同一視されます。
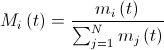。 次に、式に従って質量値を計算できます。 どこで 。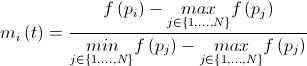
もちろん、物理的な重要性に基づいて質量を計算することはできますが、それにもかかわらず、ラシェディはこれを言っていません（私が見つけることができる著者は誰もいません）。
長所と短所
長所
- ハーモニック検索の場合と同様、実装の容易さ、
- 実際には、この方法は、実際のコーディングと従来のPSOを使用した遺伝的アルゴリズムよりも正確です。
- 実際のコーディングと従来のPSOを使用した遺伝的アルゴリズムよりも高い収束率。
短所
- 多くのパラメータを再計算する必要があるため、最高速度ではありません。
- 遺伝的アルゴリズムの突然変異と同様の手順が提供されていないため、メソッドはいくつかのローカル最適にすぐに収束し始めますので、マルチモーダル関数（特に大きな次元）の最適化中にほとんどの利点が失われます。
使用したソース
役に立つかもしれません
あとがき
これについて、おそらく、重力探索法に精通することは終了する価値があります。 この投稿が前の投稿よりも優れていることを本当に願っています。 次の投稿のトピックに投票するだけです。