通常の数字：教育プログラム

少し前に、 Piの間にデータを保存するファイルシステムについての素晴らしいユーモラスな記事に出会いました。 コメントで展開された白熱した議論（その参加者全員がジョークを理解しているわけではないようです）は、特にこのトピックが肥沃で、美しい結果、未解決の問題や他のコーシャーの事柄に満ちているので、普通の数のトピックをもっと真剣に議論するのが良いと思いました。 これらのことを知りたい場合は、猫の下に来てください。

バビロニア図書館

本の暗号に似た方法で、 児童ポルノや無許可のコンテンツを任意のデータに「格納」するのに適した番号は、 選言的と呼ばれます。 より厳密には、b-ary表記にb-ary数字の有限シーケンスが含まれている場合、その数は基本選言と呼ばれます。 このような数値は、人為的に簡単に作成できます。 たとえば、行のすべての自然数を10進数の選言数の小数部として書き出します。

0.12345678910111213 ...

わずかに少ない「人工」選言数は、シリーズの合計として取得できます。 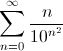次のようになります。

0,1002000030000004 ...

または、 ここで得た結果を使用して、余分なゼロの数を減らして、その量を「バビロニアライブラリ」として取得できます 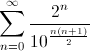次のようになります。

1.204008001600032 ...

同様の構成を使用して、任意の基準で選言数を構成できます。

レキシコン

レキシコン 、または絶対選言数は、何らかの理由で選言数です。 通常の選言番号がバビロニアのライブラリである場合、レキシコンは「バビロニアのウィキペディア」と呼ばれ、各言語セクションにバビロニアのライブラリが含まれます（番号体系）。



そのようなものを構築することはより困難です。 しかし、預言者オレグがかつて言ったように、「私の馬は危険な仕事を恐れていません」。 考え方は次のとおりです。各b桁の数字は、最初のk桁が変更されないように（bとkは任意）、特定のΔだけわずかに増やすことができます。 さらに、いくつかの数値システムでは、特定のΔminを選択して、増加してもこれらの数値システムの最初のk桁が影響を受けないようにすることができます。 したがって、レキシコンLを構築するには、次のアルゴリズムを使用できます。

1. まず、L = 0を取ります。
2. 2から∞までのnごとに、ステップ3を実行します。
3. 2からnまでの各bについて、ステップ4を実行します。
4. そのような最小Δだけ数Lを増やして、b-ary番号システムでそのレコードがb-ary番号レコード（n-b + 1）を含むようになりますが、同時にこのアイテムの以前の反復によって作成された単一のエントリは「消去」されません。
5. 限界移行をします
6. 利益！

このアルゴリズムの最初の数ステップをトレースしてみることができます。

正常性を振る

基数bの通常の数は（同じ基数の）選言数であり、kごとに、長さkのb進数字のすべてのシーケンスが、同じ漸近密度b ^-kのこの数のb進表記に含まれます。 シーケンスwの漸近密度とは 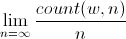ここで、 count（w、n）は、シーケンスwが最初のn桁の間で発生した回数です。



労働者と農民の用語では、同じ長さのすべてのサブシーケンスがその数字のシーケンスで等しく頻繁に見つかる場合、番号は正常です。 架空のファイルシステムのコンテキストでは、これは、同じ量のデータがほぼ同じ順序のオフセットを持つことを意味します。 冗談はさておき、オフセットレコードの長さは、このオフセットでエンコードされた情報とほぼ同じになります。 残念ながら、100％の圧縮はありません。



絶対選言数の概念と同様に、 絶対正規数の概念もあります。 ご想像のとおり、この数値は何らかの理由で正常です。

異常な正常性

驚くべきことに、私たちが日常生活で扱うすべての数値は正常ではありません。 整数の「異常性」は明らかです。整数の小数部はゼロで構成されています。 有理数も異常です。これは、ある時点で小数部分が周期的になり、この頻度と厳密に一致しない一連の数字を選択できるためです。



私たちの目に馴染みのある非合理性（pi、e、2の根など）については、それらもまたすべてがスムーズではありません。 英国の科学者は、これらの数値は正常であると考えています。 しかし、これまでのところ、私の知る限り、それらが選言的であるという証拠すらありません。



当然のことながら、通常得られる単一の「適切な」数がわからないことがわかります。 それでは、それらで何が正常ですか？ 答えは簡単です。 ほとんどの通常の数字です。 「異常な」数字のセットにはルベーグ測度0があることが証明されています。これは、単位セグメントで指を突くと、100％の確率で通常の数字に落ちることを意味します。

正規性と選言性

通常数と選言数には2つの大きな違いがあります。 1つ目は、通常の数値レコードの数字列の漸近密度に課せられる追加条件です。 第二-通常の数値の存在そのものは、それほど明白ではありません。



「バビロニア図書館」のセクションの選言数の例に戻りましょう。 2番目と3番目の例が異常であることを理解するのは簡単です。それらの例では、ゼロの漸近密度は他の数字よりも著しく高くなります。 秘密を教えましょう：



しかし、奇妙なことに、最初の例は通常の数値です。 ちなみに、この数値はChampernone定数と呼ばれます。 Copeland-Erdos定数も正常です。

0.235711131719 ...

-素数の10進エントリ​​で構成されます。 同様の定数は、他の数値システムでは正常であることが証明されています。 次のような数値の正常性：

0.1491625364964 ...

0.182764125216 ...

0.1361015212836 ...

-その他多数。 ただし、それらの正常性の証拠は簡単ではありません。 次の記事では、このトピックがhabrasocietyにとって興味深いものである場合、正常性が明らかな数値を作成する方法を示します。 これを構築する方法は非常に明白ではないので、これには別の記事が必要です（そして興味深い！）。 ハイゼンベルクの不確定性原理には、通常の数を構成することの難しさと、その正常性を証明することの難しさに関する類似点があるようです:)



絶対に通常の数については-レキシコンとは異なり、それらに対しては、構築アルゴリズムさえありません。 ただし、アルゴリズムが存在することが証明されています。 そのようなこと。

まとめ

番号Piがファイルの適切な安全性を保証しない可能性があります。 代わりに、たとえばチャンプロンの定数など、人工的に導出された通常の数値を使用することをお勧めします。 ところで、かなり興味深いアルゴリズムの問​​題は、この定数の10進表記での最初の出現のインデックスを、指定された一連の数値から決定することです。



それだけです さようなら、女の子と男の子、すぐにお会いしましょう。