正規分布（ガウス分布）は、多くの要因の影響の結果として非常に頻繁に発生するため、確率理論では常に中心的な役割を果たしてきました。 中央極限定理（CLT）は、事実上すべての応用科学に適用され、統計装置を汎用化します。 しかし、その適用が不可能な場合が非常に頻繁にあり、研究者は可能な限りあらゆる方法で結果の調整をガウス型に整理しようと試みています。 ここで、多くの要因の分布に影響を与える場合の代替アプローチを示します。
セントラルヒーティングシステムの簡単な歴史。 生きたニュートンでさえ、アブラハム・ド・モアレは、一連の独立したテストにおけるイベントの中心化され正規化された数の観測値の正規分布への収束に関する定理を証明しました。 19世紀から20世紀初頭にかけて、この定理は一般化の科学的モデルとして機能しました。 ラプラスは一様分布の場合を証明し、ポアソンは異なる確率の場合の局所定理を証明した。 ポアンカレ、ルジャンドル、ガウスは、誤差の正規分布への収束に基づいて、観測誤差と最小二乗法の豊富な理論を開発しました。 チェビシェフは、キャンペーンのモーメント法を開発することにより、ランダム変数の合計に対するさらに強力な定理を証明しました。 1900年、チェビシェフとマルコフに頼ったリアプノフは、現在の形でTSPを証明しましたが、それは3次モーメントの存在のみです。 そして、1934年になって初めて、フェラーは終止符を打ち、二次モーメントの存在が必要かつ十分な条件であることを示しました。
CLTは次のように定式化できます。ランダム変数が独立しており、均等に分布し、ゼロ以外の有限分散を持っている場合、これらの量の合計（中心化および正規化）は正規の法則に収束します。 この定理はこの形式で大学で教えられ、数学の専門家ではない観察者や研究者によって頻繁に使用されます。 彼女の何が問題なのですか？ 実際、定理は、ガウス、ポアンカレ、チェビシェフなどの19世紀の天才が取り組んだ分野、すなわち、観測誤差の理論、統計物理学、OLS、人口調査、その他の分野に完全に適用されます。 しかし、発見の独創性に欠ける科学者は一般化に従事しており、この定理をすべてに適用するか、単に存在することのできない正規分布を耳でドラッグするだけです。 あなたは例が欲しい、私はそれらを持っています。
IQ係数。 最初は、人々の知性が正常に配布されることを意味します。 彼らは、並外れた能力を考慮せず、論理的思考、精神的設計、計算能力、抽象的思考などの同じ共有要因を個別に考慮した方法で事前にコンパイルされたテストを実施します。 ほとんどの人がアクセスできない問題を解決したり、テストを超高速でパスしたりすることは考慮されておらず、テストを早くパスすると、結果が向上します（ただし、インテリジェンスはなくなります）。 そして、ペリシテ人は「誰も彼らより賢くはなれない」と信じ、「賢者から奪い去りましょう」と信じています。
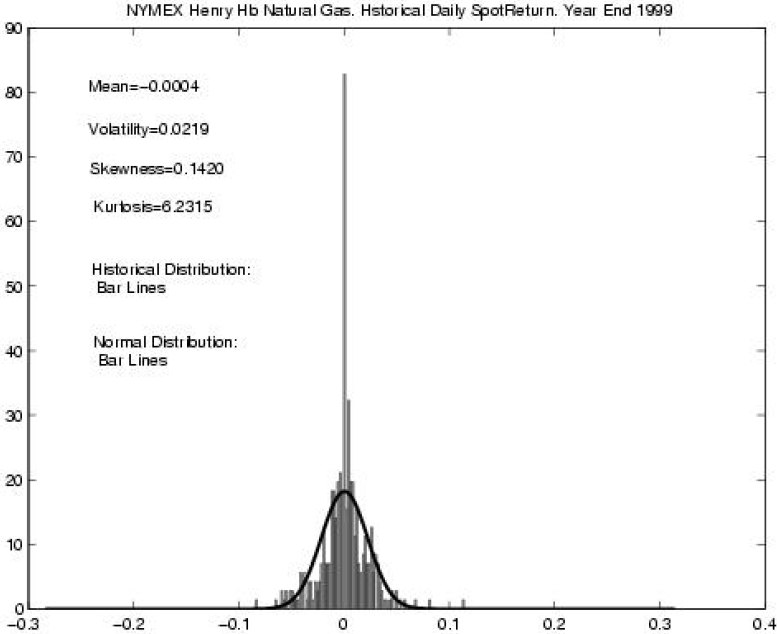
2番目の例：財務指標の変化。 株価、通貨相場、商品オプションの変化を研究するには、数学的統計を使用する必要があります。特に、分布のタイプと間違えないようにすることが重要です。 適切な事例：1997年、ストックインジケーターの成長の分布（いわゆるホワイトノイズ）が正常であるという仮定に基づいて、ノーベル経済学賞がブラックショールズモデルの提案に対して支払われました。 同時に、著者はこのモデルを明確にする必要があると明確に述べましたが、最も多くの研究者がやろうと決めたのは、ポアソン分布を正規分布に追加することだけでした。 ここで、明らかに、ポアソン分布はCLTを十分に満たしており、20項であっても正規分布と区別できないため、長い時系列の研究には不正確さがあります。 下の写真を見てください（そして、それは非常に深刻な経済雑誌からのものです）、かなり多数の観測と明らかな歪みにもかかわらず、分布が正規であると仮定されていることを示しています。
都市の人口、ディスク上のファイルサイズ、都市と国の人口の間での賃金の分布が正常ではないことは非常に明白です。
これらの例からの分布の共通の特徴は、いわゆる「重い尾」の存在、つまり、平均からかけ離れた値と、通常は正しい非対称性です。 通常の分布とは別に、このような分布が他にどのようなものになるかを考えてみましょう。 前述のポアソンから始めます：彼は尾を持っていますが、観察されるグループ（企業ごとにファイルのサイズを数え、複数の都市の給与をカウント）またはスケーリング（モデル間隔を任意に増減する）のグループに対して法則を繰り返すことを望みます黒-ショールズ）、観察が示すように、尾と非対称性は消えませんが、CLT上のポアソン分布は正常になるはずです。 同じ理由で、Erlangディストリビューション、ベータ、logonormal、およびその他のすべての分散は機能しません。 パレート分布をカットすることだけが残っていますが、サンプルデータの分析ではほとんど見られない最小値とモードの一致のために適切ではありません。
必要なプロパティを持つ分布が存在し、安定した分布と呼ばれます。 彼らの歴史も非常に興味深いものであり、主な定理は、1935年にフェラーの仕事の1年後に、フランスの数学者ポールレヴィとソビエトの数学者A.Yaの共同の努力によって証明されました。 チンチナ。 CLTは一般化され、分散の存在条件は削除されました。 通常とは異なり、安定したランダム変数の密度も分布関数も表されません（まれな例外を除き、以下で説明します）、それらについて知られているのは特性関数（分布密度の逆フーリエ変換ですが、本質を理解することはできません）知るために）。
したがって、定理：ランダム変数が独立しており、均等に分布している場合、これらの量の合計は安定した法則に収束します。
今定義。 ランダム変数Xは、その特性関数の対数が
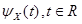フォームで想像してください：
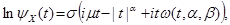
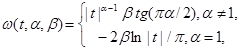
どこで
。
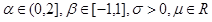実際、ここではそれほど複雑なことはなく、4つのパラメーターの意味を説明するだけです。 パラメーターsigmaとmuは通常のスケールとオフセットです。正規分布と同様に、muは数学的な期待値に等しくなります。そうであれば、アルファが複数の場合になります。 ベータパラメーターは非対称であり、ゼロに等しい場合、分布は対称です。 しかし、アルファは特性パラメーターであり、量のモーメントが存在する次数を示します.2に近づくほど、分布は通常のように見えます.2が等しい場合、分布は正規になり、この場合のみ、大きな次数のモーメントがあります正規分布、非対称性の縮退。 アルファが1でベータが0の場合、コーシー分布が得られます。アルファが半分でベータがレビー分布の場合、他の場合、そのような量の分布密度の求積法はありません。
20世紀には、安定した量とプロセス（レビープロセスと呼ばれる）の豊富な理論が開発され、それらの分数積分との関係が示され、パラメーター化とモデリングのさまざまな方法が導入され、パラメーターがいくつかの方法で評価され、推定の一貫性と安定性が示されました。 写真を見てください。その上に、フラグメントが15倍に拡大されたレヴィープロセスのシミュレートされた軌跡があります。
ブノワ・マンデルブロがフラクタルを発明したのは、こうしたプロセスと金融への応用を扱うことでした。 しかし、どこもそんなに良かったわけではありません。 20世紀の後半は、応用科学とサイバネティック科学の一般的な傾向の下を通過しました。これは純粋な数学の危機を意味し、誰もがジャーナリズムを備えた人文科学が数学の領域を占めていたが、考えたくはありませんでした。 例：American Mostellerの本「解決策を伴う50の面白い確率的確率的問題」、問題番号11：
この問題に対する著者の解決策は、単に常識の敗北です。
同じ状況は、3つの矛盾する答えが与えられる25番目の問題にも当てはまります。
しかし、持続可能な流通に戻りましょう。 この記事の残りの部分では、それらを操作する際に追加の問題がないことを示すようにします。 つまり、パラメータを推定し、分布関数を計算してモデル化する、つまり、他の分布と同じように機能することができる数値的および統計的方法があります。
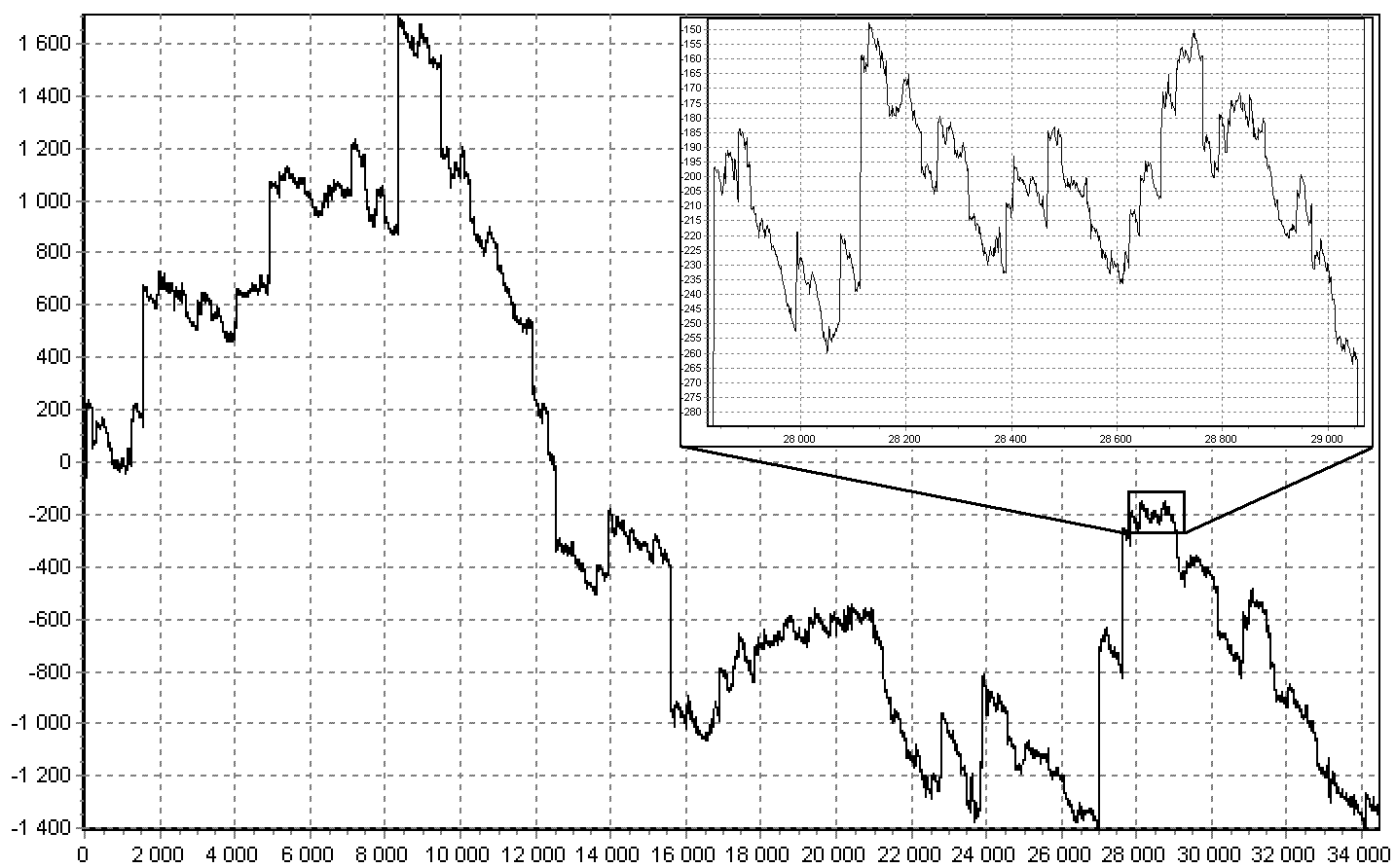
安定したランダム変数のモデリング。 すべてが比較で知られているので、計算の観点から、通常値を生成する方法（Box-Mullerメソッド）：if
基本的なランダム変数（[0、1に均一に分布し、独立している）、次に
標準の正常値が取得されます。
ここで、アルファとベータを事前定義し、 VとWを独立したランダム変数とします。Vは 、
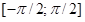、 Wはパラメーター1で指数関数的に分布し、定義します 
そして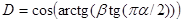 
、次に比率で：
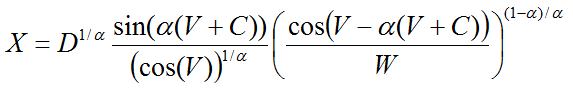
muがゼロでsigmaが1である安定したランダム変数を取得します。 これはいわゆる標準安定値であり、一般的な場合（アルファが1に等しくない場合）、スケールを乗算してオフセットを追加するだけで十分です。 はい、比率はより複雑ですが、スプレッドシート（ Link ）でも使用できるほど単純です。 以下の図は、Black-Scholesモデルのモデリング軌道を示しています。最初は正常なプロセス、次に安定したプロセスのモデルです。
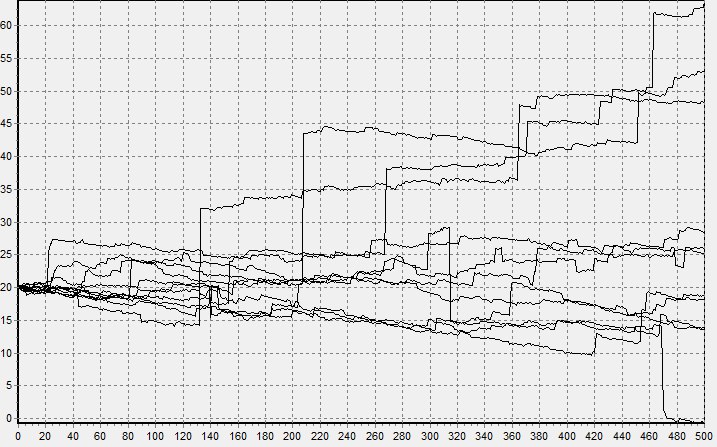
取引所の価格変更のスケジュールは、2番目のスケジュールに似ていると考えることができます。
持続可能な流通パラメーターの推定。 Habréに数式を挿入するのは非常に難しいので、パラメーターを評価するためのさまざまな方法の詳細について説明している記事 、または2つの方法しか示していないロシア語の記事へのリンクを残します。 また、安定したランダム変数とそのアプリケーションの理論全体をまとめた素晴らしい本（Zolotarev V.、Uchaikin V. Stable Distributions and their Applications。VSP。M。：1999.）、または純粋に科学的なロシア語版（Zolotarev V .M。安定した1次元分布-M .: Science、Main Edition of Physics and Mathematics、1983.-304 p。）。 密度と分布関数の計算方法もこれらの本に記載されています。
結論として、統計データを分析するとき、予想よりもはるかに高い非対称性または値がある場合にのみ、「分布法則は正しいですか？」および「すべてが正規分布で正常ですか？」