はじめに
この記事では、平面上のすべてのポイントを分析し、あらゆる種類の組み合わせを整理して、前述の形状上の制御ポイントの最適な重ね合わせを見つけることによる手書き認識の方法について説明します。 説明します。
手書きは、考えられる「ペン」で特定の図を描いています。 コンピュータシステムでの描画は、グラフィックコンテキストのすべてのピクセルに関する情報をグラフィックメモリに格納することです。 数学の「平面上の点」は抽象的な概念です。 コンピュータグラフィックスでは、この概念の背後に「ピクセル」が隠されています。 この認識アルゴリズムは、提供された一連のポイント(ピクセル)を分析し、その中で最も可能性のある類似した図を見つけようとします。 次に、図は、図を一意にするメイン(コントロール)ポイントのみを含むフレームです。
マテリエル
一般的に、アルゴリズムの中心は、一般化されたピタゴラスの定理である学校時代から知られているコサイン定理です。 平面の3つのポイントの座標とその「外観」の順序がわかれば、これらのポイントによって記述される角度を簡単に決定できます(角度の頂点は行の2番目のポイントです)。
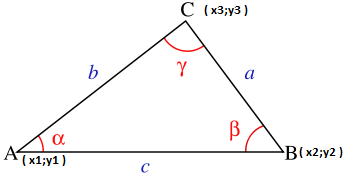
A(x1; y1)
B(x2; y2)
C(x3; y3)
点間の距離は、ピタゴラスの定理により求められます
a ^ 2 = b ^ 2 + c ^ 2-2 * b * c * cos(アルファ)
cos(アルファ)=(b ^ + c ^ -a ^)/ 2 * b * c
コサインがわかれば、角度を簡単に計算できます。
アルゴリズムの入力に供給されるポイントのセットの中で、あらゆる種類のスケルトン(上記について)のポイントを「置換」し、見つかったものの中から最適なソリューションを選択する必要があります。 これは次のように行われます。
- 図のワイヤフレームの最初と最後のポイントを取ります。 すでに2つありますが、3つ目を見つけるために残っています(角度の値を見つけるため)。
- 3番目の検索は、1番目以降のすべての後続のポイントを列挙することによって実行されます。 図の提案されたフレームにポイントを含めるという決定は、2つの分析に基づいて行われます。
- コーナーのポイント(3番目、最後のポイント)を置換し、実際の図形のフレーム内の同じ角度の値とのコンプライアンスをチェックする試み。
- 実際の図形のフレーム内の角度と同じアスペクト比で、結果の角度のアスペクト比を確認します。
これらの2つの条件が満たされている場合、アルゴリズムは、考えられるフレーム内のポイントのセットからポイントを含めることを決定します(この場合、現在の分析された数値との類似性を高めます)。
たとえば、「8」や「6」など、いくつかの分析されたフレームがある場合。 そして、認識アルゴリズムの結果:「8」-80%、「6」-90%、その後、フレーム内のコントロールポイントが多い図、つまり図8が優先されます。
ワイヤフレーム内のポイントとポイントセットの類似性の割合は単純に計算されます。ワイヤフレーム内の同じポイントと一致するすべてのポイントが合計され、関係が見つかります。 フレームにN個の制御点があり、M個の収束がある場合、類似性の割合はM / N * 100
言葉では、何かが理解できない場合があります。 したがって、ここではすべてが同じですが、明らかに(たとえば、「6」という数字):
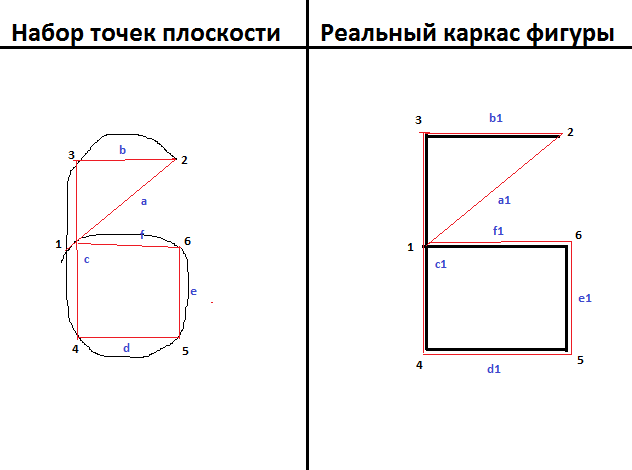
黒はポイントのセット、赤はワイヤフレームを示し、これに応じて分析が行われます。
数字は、角度のポイント(最後から開始)を示します。ポイント「2」から6を描き、ポイント「1」で終わると仮定すると、フレームの分析が始まる最初の2つのポイント-「1」と「2」、ポイント「3」を検索し、それによって形成される角度に関連するパラメータがフレーム内の同じパラメータを持つトピックと一致するようにします。 さらに、ポイント「3」を見つけたので、実際のフレームなどに従って、ポイント「4」を探します(すでにポイント「2」および「3」に依存しています)。
文字は角の側面を示します 。 つまり、アルゴリズムのルールに従って、セットのポイント(平面のポイント)を提案されたフレームに含めることができます(例)。
(角度2〜=フレーム内の角度2)そして(a / b〜= a1 / b1)そして、ポイント「3」が含まれます
(角度3〜=フレーム内の角度3)そして(b / c〜= b1 / c1)そして、ポイント「4」が含まれます
など
アルゴリズムの説明はここで終わります。
コード
言うのは簡単ですが、あなたが言う前に、言われたことをどうするかについて慎重に考える必要があります...
まあ、私はすでにC ++とOpenGLグラフィックライブラリ(+ GLUTアドイン)を使用して、発明されたアルゴリズムを考えて実装しました。 グラフィックライブラリを使用して、2次元空間に一連のポイントを描画します。 コードはそれほどではなく、それほどでもないことが判明しました。 ほとんどすべてのコードは、C ++ヘッダーファイルに広がっています。 このプロジェクトは、少なくとも少し興味がある人であれば誰でも利用できます。 ソースはBitbucketにあります。 このプロジェクトはGITバージョン管理システムを使用しているため、プロジェクトのソースコードを圧縮したい人はこれに問題はないはずです。
Figureプログラミングモードに入るには 、メインウィンドウを右クリックします。 次に、フレームを描画し(セグメントごとに順番に接続されたポイントを使用)、中央のマウスボタンをクリックします。 「完了!」が画面に表示されます。 その後、アプリケーションを再起動します。
落とし穴
ほとんどどこにいても...このアルゴリズムも例外ではありません。 率直に言って、このアルゴリズムは正しい認識での定期的な失火を許容します。
たとえば、文字「S」と「5」を考えてみましょう。失火はほとんど避けられません。 ただし、すべてのコントロールポイントが定性的に指定されていれば、ほとんどの場合、失火を回避できます。 複雑な真円度を持つ形状を分析するときにも失火が発生する可能性があります。 異なるキャラクターでミスファイアが発生した場合(たとえば、「6」と「8」でミスファイアした場合:6-100%、8-83%)、各図形のスケルトンを再度プログラムできます(繰り返し回数は制限されていません)。 これにより、認識エラーを回避できます。 そして最後に注意することは、最後、最初、2番目のポイントとアスペクト比によって形成される角度です。 これを行うには、以下のデモビデオに示すように、この角度を90度に「揃える」ことができます。
あなたが気づいたかもしれないように、記事で私は数字だけに言及しました。 しかし、実際には、認識は2次元空間のあらゆる図形に適用できます。 また、この記事の小さなアプリケーションを作成しました-アルゴリズムの動作を示すビデオです。
ご質問がありましたら、お尋ねください。喜んでお答えします。