セルゲイ・レシウク
例
そして、特定の例からすぐに始めましょう-式を数える必要があると仮定します
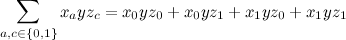
ここでは、正式に言えば、4つの項があり、それぞれ3つの要因、3つの加算と8つの乗算のみです。
素早い知恵の素晴らしさを見せて、二重和が2つの単一和の積に分解されることに注目してください。
ここでは、突然2つの加算と2つの乗算しかありません。その利点は明らかです。 おそらくご存知のように、もし私が多額を書くのが面倒なら、利益は指数関数的に増加したでしょう-項の指数数の和を小さな括弧の線形数の積に折り畳んでいます。
「ニュートンのバイノムを考えてください！」読者は私に言うでしょう。 そして彼らは正しいでしょう、それは本当にニュートンの箱に非常に似ています。 また、熱心な読者は、なぜゲームがここで必要なのか驚くことでしょう-実際、この例では明らかに余分です。
同じ例を一般化してみましょう-乗算の代わりに変数で未知の機能が発生するようにします：
同じトリックが上記に合格しますか？ いいえ、機能しません。関数の異なる値の間には関係がありません。ブラックボックスであり、括弧から外すものは何もありません。関数を4回正直に適用して結果を追加する必要があります。
トリックは中間の場合に行われます-かなり一般的な関数を考慮に入れたままにしますが、 xとyの関数とyとzの関数の積に分解すると仮定します（最終的に、 yは）：
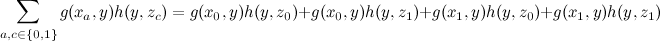
この質問の定式化により、同じように大きな合計を2つの小さな合計に分解できます。
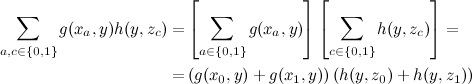
コンピューティングを大幅に節約できます。 3つの変数の関数の特定の追加構造を想定しましたが、変数xとzが完全に独立して満たされたということは真実ではないことに注意してください。それらはyを介して接続されていたため、幸いな偶然の一致により、合計する必要はありませんでした。 ところで、この合計の結果はyの関数であることに注意してください。
この例のモラルは何ですか？ 大きな関数を要約する必要があり、それがより小さな関数の積に分解される場合、括弧の積への展開が成功する可能性があります...
確率モデルへ
...しかし、これはグラフィカルな確率モデルの推論の状況です！ 最初のシリーズで説明した変数間の一貫した関係を思い出してください。
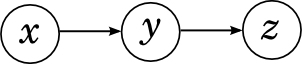
確率的な観点から、それは共同分布が次のように分解されることを意味します
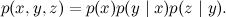
これは、3つの変数x 、 y 、およびzの関数が、単純な例とまったく同じように、 xとyの関数とyとzの関数の積に分解されることを意味します。 合計は周辺化問題に対応します。このモデルと、場合によってはいくつかの変数の値に従って、周辺確率分布を見つけます。
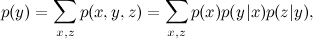
そして今、この式は
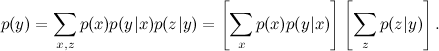
マージナル化タスクはグラフィックモデルの主なタスクであり、 前回お話ししたすべてが形式化されています：回帰重みをトレーニングする方法、既製のモデルを使用して音声を認識する方法、テストケースから認識モデルをトレーニングする方法、次のトーナメント後にプレーヤーの評価を見つける方法、軍団からの文書にトピックがどの程度含まれているかを見つける方法など。
ファクターグラフとチェーン形式のグラフ
このすべての美しさは、そのような議論が新たに毎回発明される必要はないが、一般化できることです。 最も直接的な一般化は、シリアル接続で接続されたいくつかのイベントのチェーンです。
この時点で、画像をわずかに変更すると便利です。 ここまでは変数のみを描画し、関数（確率分布）が暗示されています。 特に、大きな機能を因数分解することを意図していました。 たとえば、上の図は分解します
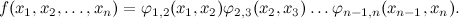
これを明示的に描画しましょう。
2種類の頂点が変数と関数に対応する2部グラフを取得しました。 各関数は依存する変数に関連付けられており、グラフ自体が大きな関数の小さな関数の積への分解を決定します。 この構造はファクターグラフと呼ばれます。これはベイズの信頼ネットワークよりも一般的な構造であり、確率的なコンテンツはなくなっていることに注意してください。分布）。
それでは、 x kに関する辺縁化問題にこのトリックを適用しましょう。 最初に、最初の量を取り込み、次に2番目、3 番目 、 …というようにk番目まで取り込みます。 結果は、合計の左側のよりコンパクトな表現であり、右側とも交差しません（長い式では申し訳ありませんが、単語よりもはるかに視覚的です）。
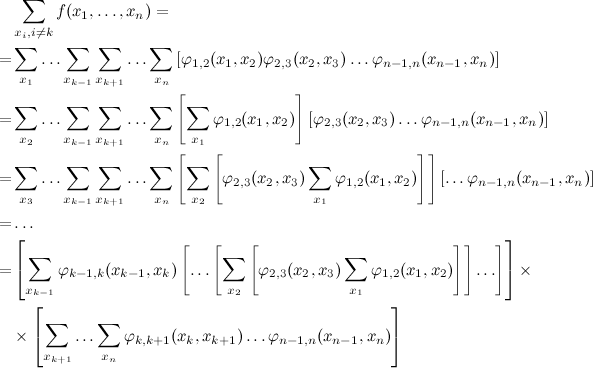
右側でも同じことができ、結果は
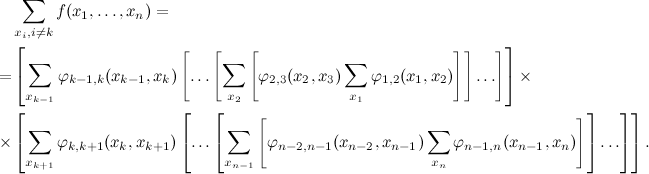
どの計算アルゴリズムが私たちのトリックに一致するかに注意してください：グラフの端から（最も内側の角かっこから）、徐々に中央（より正確にはk番目の変数）に移動し、途中で合計を折りたたみます。 これは、チェーンの両側から中央にメッセージを送信すると考えることができます。 各ステップで、基本的に同じことを行います。1つの変数h i （ x i ）の関数として以前の合計の結果を取得し、それを次のように折りたたみます。
一般的なケース
メッセージングアルゴリズムの一般的なケースは、因子グラフがツリーである （つまり、サイクルがない）場合です。 この場合、ある頂点に関する周辺化には十分であることを証明できます。
- このピークを一時的な木の根と考えてください。
- 葉からルートに向かってメッセージを送信します。 各メッセージは、正確に1つの変数の関数です。変数は、このメッセージが進むエッジに隣接しています。
- ルートに到達したすべてのメッセージを増やします。
そして、上記のメッセージを送信することがすでに可能であるときを決定するために、メッセージを送信するための非常にシンプルで包括的なルールが役立ちます：ファクターグラフの上部は、他のすべてのネイバーからメッセージをすでに受信している場合、そのネイバーにメッセージを送信できます 。 特に、リーフにはネイバーが1つしかないため、すぐにメッセージを送信し始めます。 これは、典型的なツリーでのメッセージの流れです（数字は、このメッセージが生成される「測定」を示します。現在、ボトムアップからのメッセージのみを考慮しています）。
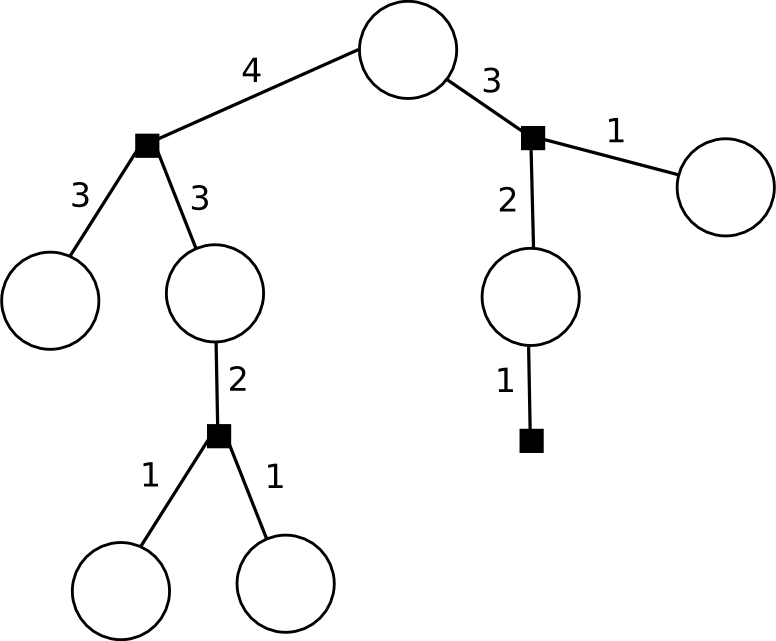
変数ノードが送信するメッセージは、受信したすべてのメッセージの単純な積です（シートの場合、同一のユニット）：
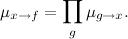
また、機能ノードのメッセージを再集計するには、部分的な周辺化を実行する必要があります。 if関数
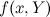すでにメッセージを受信しました 
すべての変数から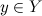 
、メッセージを変数xに渡すことができます
リスト関数はそれぞれ、自身をその唯一の隣人に転送します（製品は空です）。 ここでは、分解に関係する各関数が十分に少数の変数に依存しているため、これらの合計が「ブルートフォース」によって実行できると想定しています（突然、特に扱いにくいケースが発生した場合は、少なくとも何らかの方法で）。
次のシリーズの結論と発表
メッセージングアルゴリズムは、因子グラフがツリーの場合にのみ機能します。 因子グラフにサイクルがある場合、アルゴリズムは機能しません（サイクル以外には何もないと想像してください-どこから始めますか？）。 ただし、ファクターグラフにサイクルがまだ存在している場合、常に状況が発生します。 たとえば、最後のシリーズのテーマモデリングのLDAモデルは、通常、ほぼ完全な複数の2部グラフで構成され、各ドキュメントは各トピックに関連付けられ、因子グラフには連続したサイクルがあります。
次回は、グラフにループが存在する状況で何ができるかについて説明します。 私たちはすでに、心に留めながら、幅広い読者を対象とした人気のある記事で詳細に説明できるものの境界線に近づいていますが、次回はいくつかの直観を与えようとします。 次に、特定の例に移りましょう。