簡素化証明
そのため、前のパートでは、それらの上に新しいデータ型と関数を定義しました。 今度は、それらのプロパティと動作を定式化して証明する方法の問題に戻ります。 ある意味で、これをすでに始めています。最初の部分では、キーワード
Example
を使用して、特定の引数セットに適用される特定の関数の動作に関するステートメントを含む一種の単体テストを作成しました。 関数の定義を使用して、Coqは式を簡素化し、その左側と右側が等しいかどうかをチェックします。
この種の証拠は、かなり広範なタスクに使用できます。 0は、左側の加算演算の中立要素であることを示しています。
定理plus_O_n:forall n:nat、0 + n = n。 証明。 簡単 反射性。 Qed。
reflexivity
コマンドは、比較する前に式の両側を暗黙的に単純化します。
キーワード
simpl
および
reflexivity
は、戦術の例です。 戦術の主な目的は、必要なステートメントの正確さを検証する方法をCoqに伝えることです。 かなり狭い範囲のタスクがあり、その正確性は自動的に証明できます。 2 + 2 = 4であることを証明しましょう。
Coq <補題using_auto:2 + 2 = 4。
1つのサブゴール
==============================
2 + 2 = 4
using_auto <証明。 自動。 Qed。
証明が完了しました。
自動。
using_autoが定義されています
ほとんどの場合、戦術を使用する必要があります。
戦術intros
引数のセットに関数を適用する単体テストに加えて、定式化に数学的量指定子(「すべての自然数
n
」など)および仮説(「let
a = b
」など)が含まれるプログラムのプロパティを証明することに興味があります。 導入戦術では、量指定子と仮説をステートメントから現在の推論のコンテキストに転送でき
intros
。 ゼロによる自然数の左乗算の結果がゼロであることを証明しましょう。
定理mult_zero:forall n:nat、0 * n = 0 証明。 イントロn。 反射性。 Qed。
書き換え証明
より興味深い例を考えてみましょう:
定理plus_id_example:forall nm:nat、 n = m-> n + m = m + n。
この定理は、
n
と
m
に関して普遍的な記述を定式化して証明する代わりに、
n = m
当てはまるより狭い特性について述べています。
n
と
m
は任意の数値であるため、単純化を使用して証明することはできません。 代わりに、条件で
m
を
n
に置き換えて(
n = m
仮定)、正しいアイデンティティを取得することを証明します。 Coqにそのような変更を行うように指示する戦術は
rewrite
と呼ばれます:
証明。 イントロn m。 イントロH. 書き換え-> H. 反射性。 Qed。
ここで何が起こったかをよりよく理解するために、この例をCoqIDEで実行し、この証明を1つずつ確認することを強くお勧めします。
したがって、定理を述べて証明を開始します。

次のステップは、普遍的な量指定子と仮説の下から式を証明の現在のコンテキストに転送することです(CoqIDEの右上部分で、証明の現在のコンテキストがどのように変化するかを観察します)。
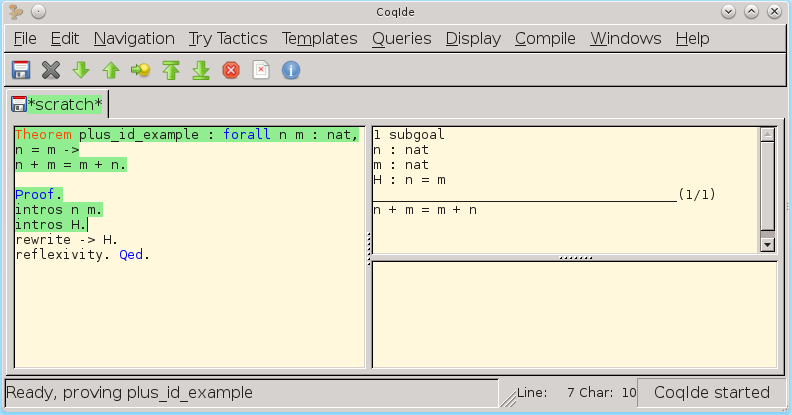
証明の現在の目的を書き換えます:
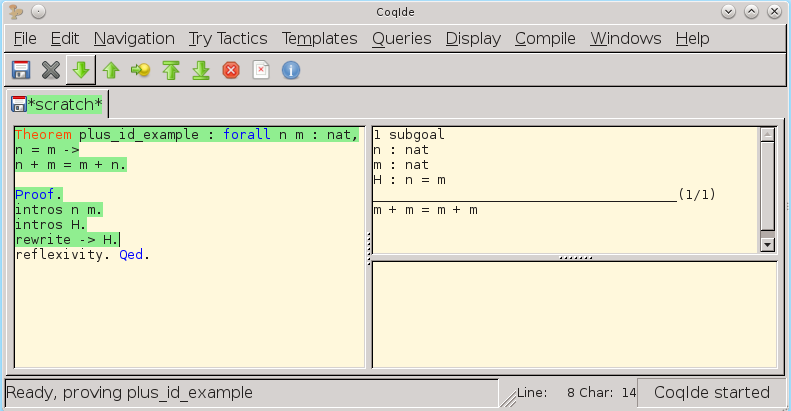
以下を単純化することにより、証明を終了します。

おわりに
次のパートでは、より高度な戦術を学び、Coqでデータ構造の操作を開始します。 繰り返しになりますが、CoqIDEでサンプルを個別に起動することの重要性に読者の注意を向けます。
前の部分へのリンク: