
先週の日曜日、ロシアコードカップの最終予選3回目が行われました。 参加したい人は誰でも来て、予選ラウンドの場所を競うことができました。
ロシアコードカップチャンピオンシップは、いくつかのオンラインツアーで構成されていることを思い出してください。その結果によると、ファイナリストは最終コンペティションにオフラインで選ばれます。
合計3回の予選ラウンドがあり、各ラウンドで200人の勝者が決定されます。 時には201人が予選の資格を得る。 これは、最後の場所が、同数のポイントを獲得した複数の参加者によって均等に分割されているためです。
予選ラウンドの勝者は予選ラウンドに参加します。 合計で600人(201人が予選ラウンドに参加した場合は603人)になります。 予選ラウンドの後、50人のファイナリストが決定されます。 この場合、最後の場所が2人の参加者によって共有される場合もあります。 この場合、51人が決勝に進みます。
予選ラウンドの約2週間が残ります。 次のラウンドを見越して、最後の予選ラウンドの結果を要約し、タスクを分析します。
タスクのテーマ:
- タスクA.試験。
- タスクB.通信。
- 問題C.世紀の試合。
- 問題D.アレイの分割。
- タスクE.森林現象。
ラウンド中、681人がログインしました。 これらのうち、少なくとも1つの決定が529人によって送信されました。
合計2660のソリューションが送信されました。
対応するタスクに最初にソリューションを送信した参加者、およびラウンド開始後の時間(分:秒):
- タスクA :イリンカ(3:59)
- 問題B :アーチ(5:18)
- タスクC :mr146(19:53)
- タスクD :megaterik(37:26)
- タスクE :peter50216(78:11)
ラウンド中に、2人のコピーリストが見られました。 彼らの結果はラウンドの終わりにすぐにキャンセルされました。 コピーリストは、ITMO専門家によって開発され、タスク検証システムに統合された特別なアルゴリズムによって識別されます。
このラウンドの参加者の領土分布は次のとおりでした。
ロシア=> 337
ウクライナ=> 81
ベラルーシ=> 42
カザフスタン=> 18
アルメニア=> 10
アメリカ=> 9
ウズベキスタン=> 4
スイス=> 4
ジョージア=> 3
ブルガリア=> 2
ラトビア=> 2
スウェーデン=> 2
ドイツ=> 2
アイスランド=> 1
トルクメニスタン=> 1
韓国=> 1
アイルランド=> 1
マケドニア=> 1
アゼルバイジャン=> 1
ルーマニア=> 1
スペイン=> 1
英国=> 1
フランス=> 1
モルドバ=> 1
キルギスタン=> 1
ポーランド=> 1
セルビア=> 1
予選ラウンドには200人が参加しました。 それらの最初の10:
- アンドレイ・マクサイ
- デニス・ムカメチャノフ
- ニックネームpeter50216を持つメンバー
- ビクター・バリノフ
- アレクサンダー・バリキン
- ミハイル・ロイズナー
- マキシム・カリニン
- エデンのローマ
- イゴール・キーロフ
- アンドレイ・ザヤキン
以下で提供するタスクの説明は、 ロシアコードカップの Webサイトでもご覧いただけます。
問題A.試験
アイデア:ニコライ・ヴェデルニコフ
実現:ニコライ・ヴェデルニコフ
分析:ニコライ・ヴェデルニコフ
タスク条件
制限時間:2秒
メモリ制限:256メガバイト
イゴールは優れたプログラマーですが、大きなずんぐりしています。 コンピュータゲームで学期全体をプレイし、多くのシリーズや映画を見た後、彼は突然、セッションの時間が来たことに気づきました。セッションは大学から飛び出さないように終了する必要があります。
イゴールは、最初の極端なプログラミング試験を受けます。 試験の本質は、ある時点Sでタスクの条件が存在するという事実にあり、それは時間Fまでイゴールが解決しなければなりません。試験は少なくとも1秒以上1日しか続きません。 割り当てられた時間内にタスクに合格した場合、イゴールは試験に合格します。 彼が試験終了後1時間以内にタスクに合格した場合、問題を解決することに加えて、テストを作成する必要があります。 そうでない場合、イゴールは試験に失敗します。
イゴールは、プログラムを何分書くかを知っており、試験に合格するか、試験にまったく合格しないか、試験に合格できるかどうかを知りたいと考えています。
入力形式
入力の最初の行には、単一の整数n(1≤n≤104)-テストの数が含まれます。 次のn行には、hh:mm:ssの形式のSとF、および整数k(1≤k≤2000)が含まれます。これは、試験の開始と終了の時刻、およびIgorがプログラムを作成する時間(分)です。
テストの時間が正しく設定されていることが保証されます。
出力形式
テストケースごとに別々の行に、問題の答えを印刷します。 イゴールが試験に合格した場合、パーフェクトを印刷します。 イゴールがテストを作成する必要がある場合は、テストを印刷します。 それ以外の場合、Failを印刷します。
例:
| 入力データ | インプリント |
| 4
01:02:03 01:05:03 3 23:12:14 00:14:59 91 00:00:00 00:00:00 1000 01:00:00 05:00:00 666 | パーフェクト
テスト パーフェクト 失敗する |
タスク解析
式60×60×hh + 60×mm + ssを使用して試験の開始時間と終了時間を秒単位で変換し、式60×kを使用してプログラムの作成に費やす時間を変換します。 次に、時間試験 =(時間終了 -時間開始 + 24×60×60)%(24×60×60)の式を使用して試験時間を計算します。時間試験 = 0の場合、実際には試験時間は24×60×60です。プログラムの執筆時間が試験の期間より短い場合、答えはパーフェクトです。 試験の作成時間が試験の期間よりも短く、1時間(60×60秒)増加した場合、答えは「試験」です。 それ以外の場合、答えは「失敗」です。
タスクB.通信
アイデア: Pavel Krotkov
実装:アンナマロバ
分析:アンナマロバ
タスク条件
制限時間:2秒
メモリ制限:256メガバイト
長年の試みの失敗の後、科学者はついに宇宙の合理的な文明との関係を確立し、エイリアンのアルファベットは2文字のみで構成されていることを発見しました:aとb。 メッセージを受信するために、送信された文字を解析できない場合は、文字a、b、および特殊文字を出力する特別な受信機が設計されました。
分析により、エイリアンはすべてのメッセージを2行の同じ行の形で送信することが示されました。 たとえば、行「abab」または「aaaaaa」はエイリアンですが、「abba」または「aaa」はエイリアンではありません。
エイリアンから潜在的なメッセージを受け取った科学者によって設計されたデバイスは、上記の特性を考慮せずに行を読み取るためのすべての可能な方法を提供します。 たとえば、文字列「ab ??」を受信すると、デバイスは「abaa」、「abab」、「abba」、および「abbb」という行を表示しますが、実際には文字列「abab」のみがエイリアンからのメッセージになり、他の3つはできません。
科学者は、デバイスの品質を改善するために、デバイスによって表示される行から何行がエイリアンからのメッセージにならないかを知りたいと考えています。 彼らがこれを行うのを助けてください。
入力形式
最初の行には、正の整数n-科学者が受け取ったメッセージ内の単語の数が含まれています。
次のn行のそれぞれには、文字a、b、および?..で構成されるメッセージの単語が含まれます。すべての単語の長さが偶数であることが保証され、各単語の長さは少なくとも1つですか?..すべての単語の合計長は200,000を超えません各単語をエイリアンからのメッセージとして解読する方法が少なくとも1つあるとは限りません。
出力形式
n行を印刷します。 i番目の行に、置換する方法の数を印刷しますか? 文字a、bで、i番目の単語がエイリアンからの正しいメッセージではないようにします。 メソッドの数は非常に多くなる可能性があるため、10 9 +7を法として出力する必要があります。
例:
| 入力データ | インプリント |
| 3
ab?b ばぁ? アッ? | 1
2 7 |
タスク解析
答えは、考えられるすべてのメッセージの数から、タンデムリピートの数を引いたものに等しいことに注意してください。 行ごとの質問数をmで、行の長さを2lで示します。 その場合、すべての可能なメッセージの数は2 mです。 タンデムリピートの数は、次の理由からわかります。 位置iに疑問符があり、位置i + l aまたはbにある場合、位置iでのタンデム反復では同じ文字である必要があります。 位置iとi + lの両方に疑問符がある場合、答えに2を掛ける必要があります。 同様に、疑問符がi + lの位置にある場合の状況を考慮します。 位置iとi + lに異なる文字がある場合、そのような行のタンデムリピートは存在しません。
ランタイムO(メッセージ長)。
問題C.世紀の試合
アイデア: Vitaly Aksenov
実現:パベル・クロトコフ
分析:パベル・クロトコフ
タスク条件
制限時間:2秒
メモリ制限:256メガバイト
毎年、銀河間物理文化と神学研究所の学生は、宇宙サッカーで「世紀の試合」を開催します。 この試合は1日中続き、研究所のすべての学部の代表チームの選手が参加します。
試合を開始する前に、審判はすべてのプレーヤーを2つのチームに分け、番号を割り当てる必要があります。 合計で2n人のプレイヤーが試合に参加し、そのうちのジャッジはランダムに選択されたn人のプレイヤーを最初のチームに、残りのn人のプレイヤーを2番目のチームに送ります。 その後、審判は両方のチームのすべてのプレーヤーに番号を割り当てます。
両方のチームのプレイヤーは数字を受け取ります。各数字は1からnまでの整数です。 同じチームのすべてのプレーヤーの数は、ペアごとに異なります。 伝統的に、最初のチームでは、プレーヤーは成長の降順で番号を受け取り、2番目では昇順で番号を受け取ります。
世紀の多くの試合を見た学生は、各試合の「娯楽」、つまり同じ数字の異なるチームの選手間のペアごとの成長の差の合計を計算するのが大好きです。 したがって、最初のチームが身長180センチと190センチのプレーヤーでプレイされ、2番目のチームが身長170センチと205センチのプレーヤーでプレイされる場合、この試合のエンターテイメントは| 180-205 | + | 190〜170 | = 45.今、彼らは「世紀の試合」の娯楽の数学的期待を計算することに興味があり、そのすべての参加者の成長を知っています。 それらを助けます。
入力形式入力の最初の行には、正の整数t-調べる必要がある世紀の一致数が含まれています。 以下は、マッチ自体の説明です。
各一致の説明は2行で構成されます。 最初の行には1つの偶数整数2n-次の「世紀の試合」の参加者の数が含まれています。 次の行には、106を超えない2nのペアごとに異なる自然数(すべての参加者の増加)が含まれています。
調査する必要があるすべての試合の参加者の総数は106人を超えません。
入力形式
入力の最初の行には、自然数t-調べる必要がある世紀の一致数が含まれています。 以下は、マッチ自体の説明です。
各一致の説明は2行で構成されます。 最初の行には1つの偶数整数2n-次の「世紀の試合」の参加者の数が含まれています。 次の行には、10 6を超えない2nのペアごとに異なる自然数-すべての参加者の増加が含まれています。
研究する必要があるすべての試合の参加者の総数は10 6を超えません
出力形式
個別の行の各一致に対して、1つの実数を印刷します-望ましい数学的期待値。 あなたの答えは正しいものと10 -6を超えて異なるべきではありません
例:
| 入力データ | インプリント |
| 1
4 20 30 10 40 | 40.0 |
タスク解析
2×n人のプレイヤーが試合に参加できるようにします。 成長の昇順に番号を付けます。 ここで、次のステートメントを証明します。必要な合計は、チームごとのパーティションで同じであり、a n + 1 + a n + 2 + ... + a 2×n -a 1 -a 2 -...-a nと等しい 再編成:数がnを超えないプレーヤーの成長は、マイナス記号で必要な量に常に含まれ、数がnより大きいプレーヤーの成長はプラスで所望の量に含まれます。
帰納法によって声明を証明します。 明らかに、n = 1の場合に当てはまります。n-1に対して有効であれば、任意のnのステートメントを証明します。成長が最小のプレイヤーがどのチームに属しているかを見てみましょう。 彼が最初のチームで終わった場合、彼はその番号nを取得します。 同じ番号を受け取った2番目のチームのプレーヤーは、試合中のすべてのプレーヤーの中で少なくとも(n + 1)番目に成長することに注意してください。 これらのプレーヤーを破棄し、その後、タスクをより小さなものに減らします。 成長が最小のプレイヤーが2番目のチームに落ちた場合も同様に考慮されます。
この声明を証明した後、問題の解決策が明らかになります。 たとえば、すべてのプレーヤーをO(n×log2n)で成長順にソートし、最初のnをマイナスで、残りをプラスで考慮することができます。
問題D.配列の分割
アイデア: Vitaly Aksenov
実装: Artem Vasiliev
分析:アルチョム・ヴァシリエフ
タスク条件
制限時間:2秒
メモリ制限:256メガバイト
1から3nまでの整数のセットを考えます。 これらの数を長さnの3つの配列a、b、cに分配して、1からnまでのiについて次のことが成り立つようにする必要があります。a i + b i = c i
入力形式
唯一の行には整数n(1≤n≤23)が含まれます。
出力形式
解が存在しない場合、最初の行に単一の数値-1を出力します。 それ以外の場合は、スペースで区切られたn個の整数をそれぞれ含む3行を印刷します。 最初の行には配列aの要素、2番目の行-配列bの要素、3番目の行-配列cを含める必要があります。 1から3nまでの各番号は1回だけ印刷する必要があります。
例:
| 入力データ | インプリント |
| 1
| 1
2 3 |
| 2
| -1
|
タスク解析
ソリューションの主なアイデアは、事前計算とカットオフ付きの列挙です。 まず、nのどの値に対して答えが存在しないかを調べます。 1から3nまでのすべての数値の合計は3n *(3n + 1)/ 2です。 一方、配列cの要素の合計をSで表します。配列aとbの要素の合計もSに等しくなります。2S= 3n *(3n + 1)/ 2、つまり3n *(3n + 1)/ 2 4で割り切れる必要があります。これは、nが4を法とする0または1に匹敵する場合にのみ当てはまります。nを4で除算した余りが2または3である場合、解は保証されません。 他のすべてのnの条件で指定された条件下で、解が存在します。
検索を高速化するには、ヒューリスティックとクリッピングを適用する必要があります。 著者の解決策は、与えられた制限の下で、解決策があれば、配列aが1からnまでの数字で満たされるという解決策があるという事実を使用しています。 このヒューリスティックにより、著者のソリューションは、1から36までのすべてのnに対して3秒で答えを見つけることができます。
問題E.森林現象
アイデア: Vitaliy Demyaniuk
実現: Vitaliy Demyanjuk
分析: Vitaliy Demyanjuk
タスク条件
制限時間:2秒
メモリ制限:256メガバイト
ベイトランドは非常に緑が多く環境に優しい国で、多くの森林、川、湖があります。 ベイトランドのすべての森林は、完全な長方形の形をしています。 i番目の森林の辺の長さはn iおよびm iキロメートルです。 各フォレストは、長方形の辺に平行な線で、辺の長さが1キロメートルに等しい正方形に分割されます。 各広場には独自のフォレスターがあります。
ご存知のように、秋には、すべてのフォレスターが冬のfireを収穫します。 しかし、この秋、想像を絶する何かが起こりました。 未知の理由で、伐採後、各フォレスターはすべての木材を無料で、同様に選択されたランダムな隣人に出荷しました。 すべてのフォレスターが同時にfireを出荷しました。 2人のフォレスターは、彼らが住んでいる森林の正方形に共通の側面がある場合、ネイバーと呼ばれます。
各森林の人間の行動のこの現象をより詳細に研究するには、この手順の後に冬のために少なくともいくらかのfireを持っているフォレスターの数の数学的な期待を計算する必要があります。
入力形式
最初の行には、正の整数t-ベイトランドの森林の数が含まれています。
次のt行のそれぞれには、2つの数値n iおよびm iが含まれます。これは、i番目のフォレストの辺の長さです。 (1≤n i≤10 7、1≤m i≤10 7 nm≥2)。
Baytlandの森林の数は10,000を超えません。
出力形式
各フォレストについて、別の行に、望ましい数学的期待値を既約分数の形式で出力します。 分子と分母は、追加のスペースなしで/で区切る必要があります。 分母が1に等しい場合、分子のみが表示されます。
例:
| 入力データ | インプリント |
| 2
13 45 | 2
2015/144 |
タスク解析
fireの分布の可能なシナリオの1つを指定しましょう。 l i、j (x)は、座標iとjの正方形に住んでいるフォレスターに冬用のhasがある場合は1、それ以外の場合はゼロである関数として定義します。 冬にfireを持っているフォレスターの数は、森林のすべての正方形の合計l i、j (x)に等しくなります。 次に、数学的期待値の線形性に従って、必要な期待値は、森林のすべての平方にわたる数学的期待値l i、jの合計に等しくなります。 数学的な期待値l i、jを見つける:E(l i、j )= 0×p i、j + 1×(1-p i、j )= 1-p i、j 、ここでp i、jは確率対応するフォレスターには冬用のfireがなかった。 フォレスターが対応する隣人からfireを受け取らなかったイベントの確率の積としてp i、jを計算することができます。
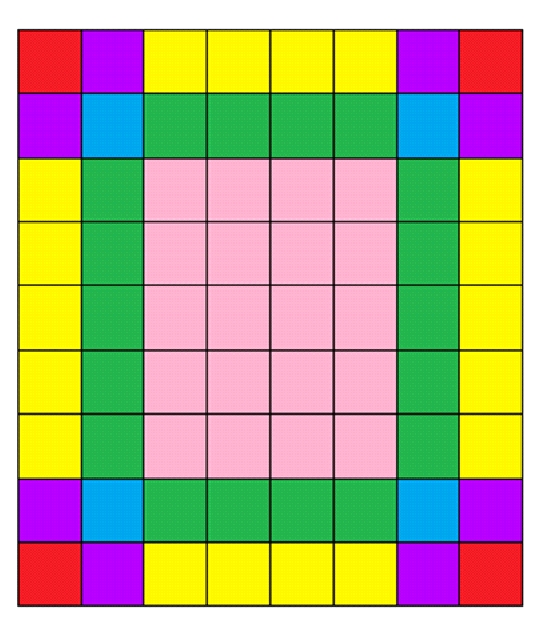
上の図では、同じ色の正方形の場合、p i、jは等しくなります。 したがって、タイプごとに、セルの数を計算し、それに対応するpi、jを掛けてから、すべてを追加する必要があります。 6つのタイプしかないため、プログラムの動作時間はO(1)です。 また、辺の小さい方が1、2、または3に等しい場合を個別に考慮する必要があります。
次のRCC予選ラウンドは6月16日に開催されます。 タスクの分析を公開します。 お楽しみに!