ほとんどの場合、潤滑経路は直線であると想定されており、そのパラメーターはユーザー自身が設定する必要があります-これにはコアの選択に非常に骨の折れる作業が必要です手で選ぶのは難しい。

過去数年間、画像復元の理論における新たな方向性が集中的に開発されています-ブラインドデコンボリューション。 このトピックには非常に多くの作業が含まれており、結果の積極的な商用利用が開始されています。
多くの人がAdobe MAX 2011カンファレンスを覚えています。そこではブラインドデコンボリューションアルゴリズムの1つの操作を示しました: Photoshopの新しいバージョンでぼやけた写真を修正してください
この記事では、この驚くべき技術がどのように機能するかをさらに詳しく説明し、SmartDeblurの実用的な実装も示します。SmartDeblurでは、このアルゴリズムも自由に使用できます。
注意、カットの下にたくさんの写真があります!
開始する
この投稿は、ぼけた画像とぼけた画像の復元に関する一連の私の投稿の続きです:パート1.理論-焦点がぼけた画像とぼけた画像の復元
パート2.練習-焦点がぼけてぼやけた画像の復元
パート3.品質の改善-ピンぼけおよびぼやけた画像の復元
畳み込み、逆畳み込み、フーリエ変換、およびその他の用語が何であるかをよりよく理解するために、少なくとも最初の理論部分を読むことをお勧めします。 3番目の部分が最後になると約束しましたが、抵抗することはできず、画像修復の分野の最新の傾向については伝えませんでした。
ブラインドデコボリューションは、アメリカの教授Rob Fergusの作品「一枚の写真からカメラシェークを取り除く」の例として考えます。 元の記事は彼のページにあります: http : //cs.nyu.edu/~fergus/pmwiki/pmwiki.php
これは最新の作品ではなく、最近では最良の結果を示す他の多くの出版物がありますが、多くの段階で非常に複雑な数学を使用し(準備ができていない読者向け)、基本的な原理は同じです。ある種の「クラシック」である彼は、非常に複雑なケースでも潤滑剤コアを自動的に検出できる、根本的に新しいアプローチを提案した最初の1人でした。
歪みモデル
それでは、始めましょう。カメラを取り、ぼやけたショットを撮ります-これに適していますが、それほど労力を必要としません:)

次の表記法を紹介します。
B-観察されたぼやけた画像
K-コアブラー(軌跡スミア)、カーネル
L-元のぼやけた画像(非表示)
N-加法性ノイズ
次に、スミア/歪みプロセスは、次の式として説明できます。
B = K * L + N
記号「*」は畳み込み演算であり、通常の乗算と混同しないでください!
畳み込みとは、 最初の部分で読むことができます
視覚的な形式では、これは次のように表すことができます(簡単にするためにノイズ成分を省略します)。

それで、最も難しいのは何ですか?
単純なアナロジーを想像してください-数字11は2つの要素で構成されています。 彼らは何ですか?
ソリューションは無限です。
11 = 1 x 11
11 = 2 x 5.5
11 = 3 x 3.667
など
または、視覚的な表現に移ります:

対象機能
特定のソリューションを得るには、制限を導入し、何とかして私たちが目指しているモデルを説明する必要があります。つまり より多くの情報が必要です。 このためのオプションの1つは目的関数を設定することです。これは、値が高い関数(単純な場合)であり、結果が目的の関数に近くなるほど関数になります。
研究により、実際の画像は個々のピクセルの値に大きな広がりがあるにもかかわらず、これらの値の勾配は境界が緩やかに減少する分布( ヘビーテール分布 )の形をとることが示されています。 このような分布はゼロ付近にピークを持ち、ガウス分布とは対照的に、大きな値(バターなど)の確率が大幅に高くなります。
これは、ほとんどの場合、実際の画像にはほぼ一定の明るさの大きな領域があり、最終的には明るさが中程度のシャープな差があるオブジェクトであるという直感的な考えと一致します。
これは、鮮明な画像の勾配ヒストグラムの例です。
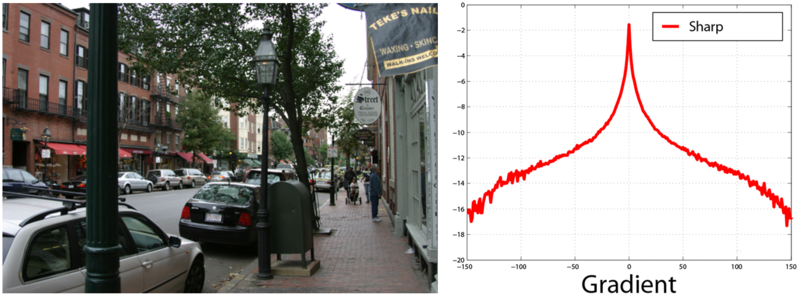
ぼやけた画像の場合:
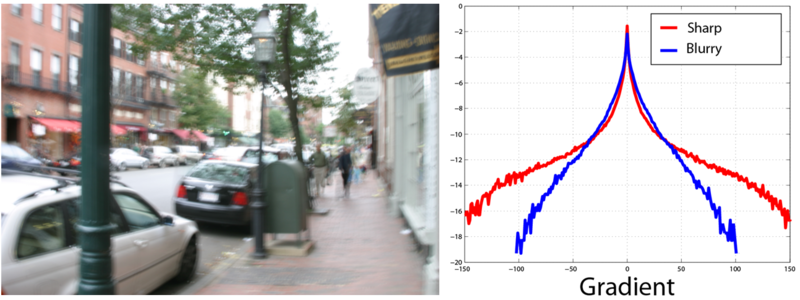
したがって、結果の「品質」を実際の画像との明瞭さと類似性の観点から測定できるツールを入手しました。
これで、完成したモデルを構築するための主要なポイントを定式化できます。
1.歪みモデルによって課せられる制限B = K * L + N
2.再構成結果の目的関数は、勾配のヒストグラムが境界がゆっくりと減少する理論分布にどれだけ似ているかです。 p(L P )で表す
3.歪みコアの目的関数は正の値であり、白いピクセルの割合が低い(スミアパスは通常細い線で表されるため)。 p(K)で表す
次のように、これらすべてを共通の目的関数に結合します。
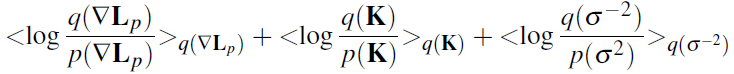
ここで、 q(L P ) 、 q(K)は 変分ベイズ法によって得られた分布です。
さらに、この目的関数は、いくつかの追加を伴う座標降下の方法によって最小化されますが、その複雑さと数式の豊富さのために説明しません-これはすべてFergusで読むことができます。
このアプローチにより、既存のコアの品質を改善できますが、このコアをゼロから構築することはできません。 最も可能性の高い解決策を見つけるプロセスでは、ローカルミニマムの1つに分類されます。
ピラミッド型アプローチ
この問題の解決策は、歪みコアを構築する反復アプローチです。最初に、入力のぼやけた画像とは異なる解像度の画像のピラミッドを構築します。 最小サイズから元のサイズまで。
次に、3×3カーネルを使用して、単純なパターンの1つである垂直線、水平線、またはガウススポットを使用してアルゴリズムを初期化します。 普遍的なオプションとして、後者-ガウススポットを選択できます。
上記の最適化アルゴリズムを使用して、構築されたピラミッドの最小画像サイズを使用してカーネル推定を改善します。
その後、結果の更新されたカーネルのサイズを、たとえば5 * 5ピクセルに変更し、次のサイズの画像で既にプロセスを繰り返します。
したがって、各ステップでコアをわずかに改善し、その結果、潤滑剤の非常に正確な軌道を取得します。
例を使用して、カーネルの反復構成を示しましょう。
元の画像:

カーネル改良プロセス:

1行目と3行目は、画像ピラミッドの各レベルでのカーネルスコアを示しています。
2行目と4行目は、歪みのない画像の推定値です。
結果:

フローチャート
すべてを一緒に収集し、アルゴリズム全体を記述することは残ります。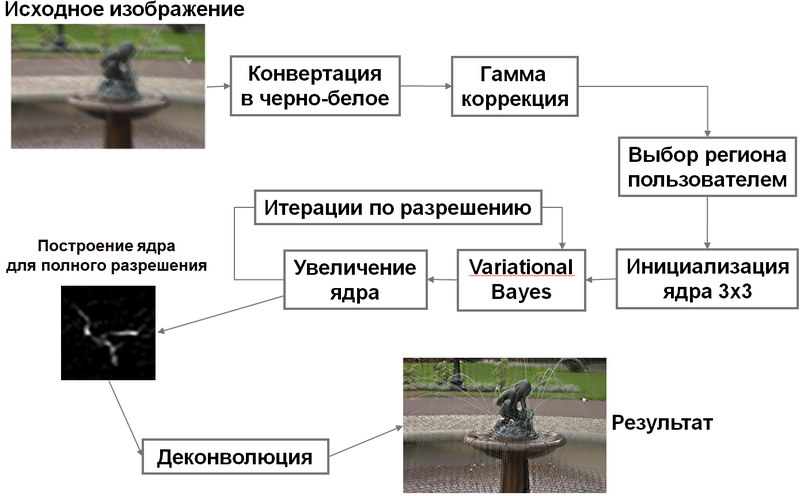
より現代的なアプローチは、カーネルの順次改良というほぼ同じ考えを持っていますが、再構成結果と歪みカーネルのために目的関数のより洗練されたバージョンを使用します。 さらに、結果のコアの中間および最終フィルタリングを実行して、過剰なノイズを除去し、洗練アルゴリズムのいくつかのエラーを修正します。
実用的な実装
おそらく最も興味深いのは、実画像上でライブのブラインドデコンボリューションアルゴリズムを試してみることです!同様のオプションを実装し、SmartDeblur 2.0の新機能として追加しました-すべて無料です:)
プロジェクトのアドレス: smartdeblur.net
( 以前のバージョンのソースとバイナリはGitHubで見つけることができます: github.com/Y-Vladimir/SmartDeblur )
作業例:

別の例:
 |  |
 |
最後に、Adobe MAX 2011カンファレンスの画像に関する作業の結果:
 |  |
 |
ご覧のとおり、結果はほぼ完璧です。Adobeのデモとほぼ同じです。
技術的な詳細
これまでのところ、処理された画像の最大サイズは1200 * 1200に設定されています。 これは、アルゴリズムが多くのメモリを消費するという事実によるものです。 1000ピクセルの画像でも1ギガバイト以上です。 そのため、サイズ制限が導入されました。デコンボリューションとピラミッド構造を最適化した後、後で増やします。
インターフェイスは次のとおりです。
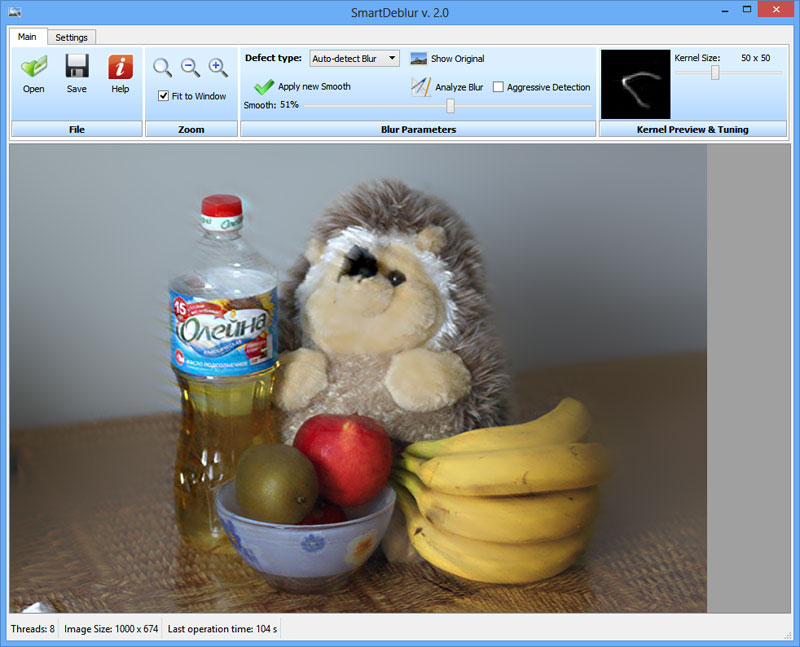
このプログラムを使用するには、画像をダウンロードして[ぼかしの分析]をクリックし、画像全体を選択するだけで済みます。分析には数分かかる場合があります。 結果が自分に合わない場合は、別の領域を選択できます(画像内でマウスを使用して上下に移動することは、少しわかりにくいですが、これまでのところ:))。 右ボタンで選択を選択します。
「積極的な検出」チェックボックスは、カーネルの最も重要な要素のみを選択するように設定を変更します。
これまでのところ、すべての画像で良い結果が得られるにはほど遠いです。したがって、フィードバックに非常に満足しています。これはアルゴリズムの改善に役立ちます。
--
ウラジミール・ユジコフ(ウラジミール・ユジコフ)