アカデミック大学の理論計算機科学

アカデミック大学のrog慢で自己陶酔的な学生の話を説明したいのですが、もちろんそうではありませんが、彼の考えや経験については良い考えがあります。 たとえば、この生徒をShurikと呼びます。 Shurikがアカデミック大学（AU）に入学したとき、彼のプログラミングの履歴書によれば、彼はすでにアルゴリズムの分野の専門家でした。 彼は、詳細な検索アルゴリズムを巧みにマスターし、配列をソートするためのいくつかの方法を知っていて、バイナリ検索についてのアイデアを持ちました。 当然のことながら、アルゴリズムのコースは彼にはまったく興味がなく、実際、5年の経験を持つプログラマーにはほとんど教えられません。 AUの理論情報学のプログラムは、彼が知っている主題のトピックに彼には未知の言葉が多すぎるという事実に興味を持っていました。 しかし、これはピーターであり、彼らはおそらく縁石を奇妙な言葉と呼び、美しい言葉の深さを探すためにそれを考えました。 彼はコースのスライドとビデオを注意深く研究しました。 そこにはある種のコンピューターサイエンスがあり、Shurikはそれを完全には所有していないことが判明しました。 シュリックは本、靴下、5年間の経験を収集し、ピーターにインタビューのために行きました。 そこで彼は、そのような経験を持つプログラマーにさえ何かを教えることができる人々に会いました。 これはすべて、シュリコフの世界像を破壊しました。この世界では、コンピューターサイエンスの知識はC＃で書かれたクラスの数で測定されていました。

大学院での研究中に、シュリックは回路の複雑さの分野と指数アルゴリズムの分野の研究に従事していました。 これは本当に興味深いものであり、大学院に入学する際にも重要です。

現時点では、シュリックはニューヨーク大学の幸せな大学院生であり、「縁石」という言葉を使用し、 アカデミック大学に深い感謝の念を抱いています。 そして、自治大学の数学および情報技術学科は、現在、特に「理論的情報学」の方向で、一連の新しい学部生を率いています。

今、私はシュリックにその言葉を伝えます。シュリックは彼の研究の1つについて話します。

NP困難問題のアルゴリズム

NP困難問題は、実際に頻繁に遭遇するタスクであり、効果的な解決アルゴリズムは不明です。 そのような問題の研究は非常に興味深いものです。 これらの問題のいずれかに対する有効なアルゴリズムの存在は、クラスNPのすべての問題に対する有効なアルゴリズムの存在を意味します。 逆に、これらの問題の少なくとも1つに効果的なアルゴリズムがないことを証明できれば、これはすべてのNPハード問題にそのようなアルゴリズムが存在しないことを意味します。 AUの行政では、NP困難な問題を解決するための正確かつ近似のアルゴリズムを調査しました。 たとえば、最大実現可能性の問題、巡回セールスマンの問題、最短の共通上部構造の問題を解決するための新しいアルゴリズムを取得することができました。 次に、これらのアルゴリズムの1つ、つまり巡回セールスマン問題の近似解法のアルゴリズムについて説明します。



NPハード最適化問題はNPハード問題であり、すべての可能な解決策の中から、何らかの意味で最適な解決策を選択する必要があります。 たとえば、特定の重み付きグラフの各頂点を1回だけ通過する最短サイクルを見つけます。 おそらく、各頂点を1回だけ通過してグラフを回避する方法は多数ありますが、重みが最小のラウンドにのみ関心があります。 このタスクは巡回セールスマン問題と呼ばれます。 このタスクの最悪の既知のアルゴリズムは、ほぼ同時に実行されます。 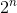。 この種のタスクのアルゴリズムの高速化に取り組みました。 たとえば、時間内に機能するアルゴリズム 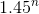、nの大きな値の問題を解決します。 1000倍高速で動作するコンピューターを購入しても、実行時の指数が小さい新しいアルゴリズムのような高速化は得られないことに注意してください。 この問題に対する多項式アルゴリズムの存在は、クラスPとNPの同等性を必要とし、そのようなアルゴリズムの欠如の証明は、これらのクラスが同等ではないことを意味します。

巡回セールスマン問題

グラフのハミルトニアンサイクルは、グラフの各頂点を1回だけ通過するサイクルです。 巡回セールスマン問題 （ TSP ）は、所定の重み付きグラフで最小重みのハミルトニアンサイクルを見つけることです。 元のグラフの頂点の数をnで、エッジの最大重みをMで表します。 巡回セールスマンの問題を実際に解決する方法は数多くありますが、この記事では、最悪の場合のランタイムの証明可能な推定値を持つ理論的アルゴリズムについてのみ説明します。

巡回セールスマン問題を解くための正確なアルゴリズム

1962年に、TSPを時間内に解決する動的プログラミングアルゴリズムが開発されました。 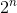しかし、指数関数を使用して 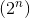メモリ。 多項式メモリのみを使用する最も有名なアルゴリズムにはランタイムがあります。 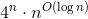。 中間結果も、たとえば、 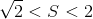、時間とともに問題を解決するためのアルゴリズムがあります 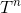メモリを使用し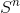て どこで 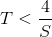。 問題を時間内に解決する包含例外式に基づく既知のアルゴリズム 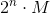メモリを使用して 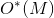。 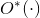入力長から多項式因子を隠します、すなわち 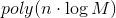。 TSPの非指向の場合には、動作時間のあるモンテカルロアルゴリズムがあります。 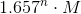そして、指数関数的に小さいエラーの確率。



50年以上にわたって、次の質問が開かれています。

1. ランタイムを備えたTSPのアルゴリズムの存在 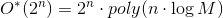および多項式メモリ。
2. ランタイムを備えたTSPのアルゴリズムの存在 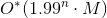巡回セールスマン問題の一般的な（指向の）ケースの場合。

巡回セールスマン問題を解決するための近似アルゴリズム

仮定の下で知られている 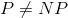、合計TSPを多項式で計算可能な因子で近似することはできません。 つまり、この仮定では、最適解の10近似だけでなく、n！近似を見つけることも不可能です。 グラフのエッジの重みが三角形の不等式を満たす特別なケースは、 メトリック巡回セールスマン問題と呼ばれます 。 無指向の計量問題については、1.5近似が知られています。 しかし、この特定のケースでは、仮定の下で 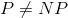、近似の良い多項式アルゴリズムを見つけることができません 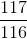（指向の場合- 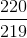） 問題の指向メトリックバージョンでは、近似係数が最近改善されました。 。

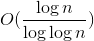指数時間アプローチ

固定のアルゴリズム 使用する 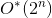計算のためのステップと多項式メモリ 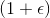指向のメトリック巡回セールスマン問題の概算。 上記のように、TSPの非指向メトリックバージョンでも、最もよく知られている多項式近似は1.5です（指向の場合 ）

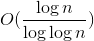もし 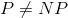、その後、多項式時間については見つけることができません 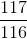-非指向のメトリックTSPの概算。

たとえば、必要な場合 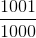-近似、その後、指数メモリまたは時間を必要とする正確なアルゴリズムを使用する必要があります 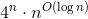。 指数アルゴリズムは実際にはめったに使用されませんが、いずれにしても、それらを実行して回答を待つことができます。 ただし、アルゴリズムが指数メモリを使用する場合、妥当なサイズの入力でアルゴリズムを実行することさえできません。

提案されたアルゴリズムは見つけることができます 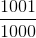-経時的な合計TSPの概算 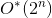多項式メモリのみを使用します。



開発されたアルゴリズムは、 Ibarra、Kimの研究でバックパック問題の完全多項式近似スキームを構築するために提案されたアイデアを使用しています。 作成者は、時間とともに機能するバックパック問題に擬似多項式アルゴリズムを使用します 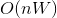ここで、nはアイテムの数、Wはバックパックの容量です。

バックパック問題の完全な多項式近似スキームは、最初にすべてのオブジェクトの重みを 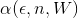、次に擬似多項式アルゴリズムを呼び出します。 受信した回答は最適ではない可能性があります、なぜなら いくつかの重みは単に分割されていません 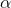また、丸められます。 ただし、単純な分析では、丸めが結果に大きな影響を与えないことが示されています。



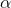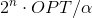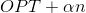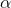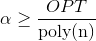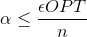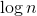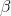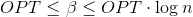同様のアイデアを使用します。 OPTにより、最適解TSPを示します。 メモリアルゴリズムから近似多項式を取得するには、まずすべてのエッジの重みを十分に大きい数に分割します 、包含包含式に基づいて正確なアルゴリズムを実行します。 結果のアルゴリズムの実行時間は次と等しくなります そして、結果のサイクルの長さはもうなくなります 。 今、私たちは選択したい そのように そして 。 TSPのメトリックバージョンは、たとえば次の係数を使用して、多項式時間で近似できます。 。 つまり、見つけることができます あれ そして取る 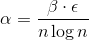。 次に、結果のアルゴリズムにはランタイムがあります 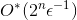そしてメモリを使用する 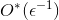。 また、この結果を一般的な（非メトリック指向の）巡回セールスマン問題のケースに一般化することもできました。