レッスンマキシマ
はじめに
Maximaは、Common Lispに基づいた無料のコンピューター代数システム(CAS)です。 機能的には、Mathcad、Mathematica、Mapleなどの他の最新の有料CASよりも劣っていません。 分析(記号)計算、数値計算、グラフ作成(gnuplotを使用)を実行できます。 スクリプトを記述し、それらをCommon Lispコードに変換してからコンパイルすることもできます。 言語はLispプログラマーによって開発されたものから作成されたという事実を考慮すると、その構文はやや紛らわしいように見えるかもしれません。 これらの点を正確に明確にし、アクセス可能な方法で機能的アプローチの本質を説明しようとします。特定の数学関数にはまったく焦点を当てません。それらは独立して習得するのは非常に簡単です。 この記事では、微積分の機能と構文構造の最大値を正確に説明します。
シェル
もちろん、コンソールからmaximaインタープリターを呼び出すことはあまり便利ではありません。 ラテックスでレンダリングされた美しいフォーミュラを見てみたいです。 したがって、初心者の場合、 wxMaximaシェルを配置することをお勧めします。 TeXmacsが好きなら-シェルとして設定できます(正直なところ、私は試していません)。 まあ、emacsの愛好家には、バッファーで動作するimaximaがあります。 文字通り箱から出しています。
知人
一見、すべてがシンプルです。セミコロンで終わる表現を導入し、答えを取得します。 電卓として最大値を試したり、2つの数値の合計を計算したり、角度のサインを計算したりできます。 私たちは何が起こっているかをより深く掘り下げます。
原子
シンボル、数値、および論理定数trueおよびfalseは、システム内で最も単純なオブジェクトです。 言語の他のすべての式と構造はそれらから構築されるため、それらはアトミック(不可分)または単にアトムと呼ばれます。
変数

システムは、自由変数とシグナル変数を区別します。 示されている変数は関連変数であり、値が割り当てられている変数です。 解釈するとき、変数の名前はその値に置き換えられます。 「:」記号を使用して変数を設定できます。 自由変数はどの値にも関連付けられておらず、抽象的に操作できます。たとえば、2つのシンボリック式を追加します。
計算コンテキスト
各コマンドを計算すると、その計算コンテキストが形成されます。 これは、変数名とその値、およびいくつかの解釈パラメーター間の関係のコレクションです。 ローカルとグローバルの2つの計算コンテキストがあります。 グローバルコンテキスト-すべての解釈されたコマンドに共通して、インタープリターの現在の状態を決定します。 ローカルコンテキストは、1つのコマンドの実行中に作成され、それに対してのみ有効です。 最も高い優先順位は、接続とローカルコンテキストのパラメーターです。

ここでは、変数aの値はグローバルコンテキストから取得され、ローカルコンテキストの場合、作品を展開するオプションが確立されます。 今後の作業は、それ自体では展開されません。
計算ロック

2つの変数を追加してみましょう。 そして、それらの前に一重引用符を置きます。 これはブロッキング演算子です。 変数名の前に配置した場合-結果として、関数呼び出しの前にこの変数の名前を取得します-関数呼び出しのシンボリック式。 なんで? たとえば、不定積分の計算など、ある関数を使用して別の関数の式を処理し、出力として関数または数値を取得する必要がある場合があります。 つまり、式をデータとして表現して操作することができます。 ただし、2つの数値の合計の計算を停止しようとしても、計算は停止しません。 これは、単一引用符演算子が式の最も単純な単純化(数値の単純な操作、分数の削減)を停止しないという事実によるものです。 また、有理(浮動)引数の関数の値を計算しようとしても、計算は停止しません。
そして、Maximaシステムはアルゴリズム関数と数学関数を区別しません。それらは1つの言語要素です。 インタプリタ自体の用語では、計算可能な演算子は動詞と呼ばれ、計算されていない形式のままである演算子は名詞と呼ばれます。 すべての名詞の計算を開始するには、計算のコンテキストで名詞オプションを設定する必要があります。

計算
インタプリタがシンボリック式の概念とその計算を区別することを学びました。 どのような場合に計算が行われますか? 最も明白なケースは、ある種の式(たとえば、2 + 3)を計算しようとした場合です。 彼らは表現に入りました-その意味を得ました。 彼らは引数の関数を計算しました-値を得ました。 変数名を入力し、その値を取得します。 変数の値は、アトムまたはシンボリック式のいずれかであることがわかった。 計算はいつですか? 変数に値が割り当てられると、計算が行われます。 コロンの右側の値は割り当ての前に計算されるため、変数をシンボリック式に割り当てる場合、引用符を付けてこの計算を停止します。 右側の式と左側の式の両方が評価される場合、特別な種類の割り当て(2コロン演算子)があります。 また、関数を評価する前に、すべての引数が計算されます。

左側の変数aの計算結果は変数bです。
例
簡単な例を考えてみましょう-すべてのサブセットのセットを構築します。 判明したように、Maximaにはセットを操作するための組み込み型がありますが、残念ながら、そのような機能はありません。 書いて
まず、セットが何であるかを見てみましょう。 Maximaのセットは、異なるデータ構造(単一リンクリスト)に基づいているようです。 誰もが理解できるリストとは何ですか。 それらには、3つの主な機能があります:リストの先頭の要素を受け取る(最初)、最初の要素を含まない元のリストを受け取る(rest)、新しい要素を先頭に追加する(cons)、2つのリストを組み合わせる(append) 同様の関数はどのLisp実装にも存在しますが、ほとんどの場合、それぞれ異なる呼び出しが行われます:それぞれcar、cdr、cons、append。
このような問題を解決するためのアルゴリズムを通常どのように想像しますか? サブセットを特性ベクトルの形式で表現し、それらすべてを反復処理できます。 ただし、機能的なアプローチを正確に示します。 各要素がサブセットのちょうど半分に含まれていることは簡単にわかります。 この単純な事実は、再帰アルゴリズムを構築するのにすでに十分です。 集合Aから1つの要素aを削除します。Aのすべてのサブセットの集合は、すべてのサブセットA \ aの集合とすべてのサブセットA \ aの集合で構成され、aが各要素に追加されます。 最後のステートメントを使用すると、問題の次元を再帰的に任意に下げて、些細なケースに減らすことができます。 実装には、指定された要素を各セットに追加する2つのパラメーター(要素とセットのセット)の追加機能が必要です。

関数の宣言は数学のように発生することに注意してください。 符号が計算されなかった後に正しい部分を決定する際に注意する必要があります。 (関数の定義が計算されるように関数を定義するには、定義フォームを使用します)。 ここに新しい計算形式があります。 命令型言語と同じように機能します。 条件が満たされると、式はthenの後に評価され、そうでない場合はelseの後に評価されます。 次に、目的の関数を作成します。
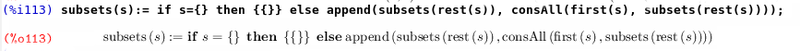
数えるために何かを試してみましょう。

終わり
まあ、それだけです。 次の記事では、最急勾配降下法の実装について説明するとよいでしょう。