Haskellの日本語クロスワードソリューション

日本のクロスワードパズル-数字のセットを使用して、元の白黒画像を再現する必要があるパズル。 ピクセルの各行と各列には独自のセットがあり、各番号は連続する黒ピクセルのブロックの長さに対応しています。 このようなブロック間には少なくとも1つの白いピクセルが必要ですが、正確な数は不明です。 これらのパズルに完全に捧げられた雑誌はほとんどのニューススタンドで見られるので、ほとんどすべての雑誌は少なくとも一度は会ったことがあるので、ここでは詳細な説明を省略することができます。



ある時点で、日本のクロスワードを自分で解決する方法を「コンピューターに教える」ことを望んでいました。 高尚な目標はない、ただの楽しみのために。 その後、人間の脳の能力が限られているために私自身は適用できない方法が追加されましたが、公平に言えば、プログラムはそれらのない雑誌のすべてのクロスワードに対応しています。



そのため、タスクは簡単です。クロスワードパズルを解き、多くの解決策があれば、それらをすべて見つけてください。 ソリューションはHaskellで書かれており、言語の知識がなくてもコードは言葉による説明を実質的に補完しますが、一般的な本質は理解できます。 結果をライブで確認したい場合は、プロジェクトページでソースをダウンロードできます（バイナリアセンブリはアップロードしませんでした）。 ソリューションはバイナリPBMにエクスポートされ、そこから条件を抽出できます。







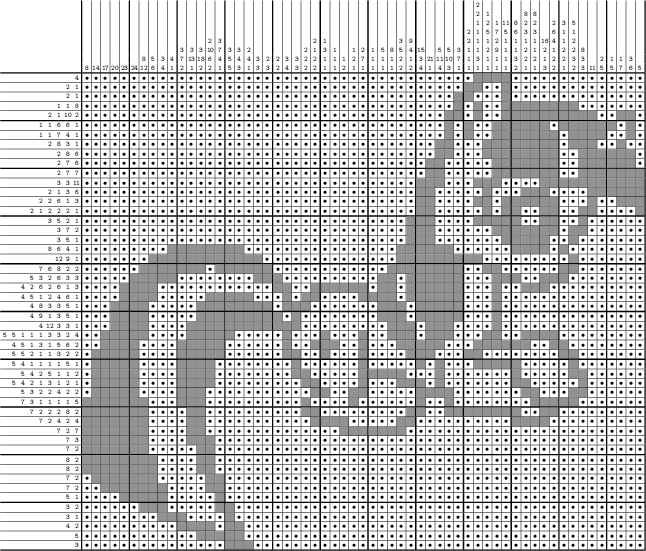
できるだけ明確に書き込もうとしたにもかかわらず、完全には成功しませんでした。 カットの下に多くの文字とコードがあり、写真はほとんどありません。

ビットマスク

プログラム全体は、ビットマスクの自転車に基づいています。 速すぎませんが、デバッグプロセスで重要なプロパティがあります。意味のない操作、つまり異なる長さのマスクの操作中にクラッシュします。 ここでは、関数の署名とその機能の原理を説明する写真のみを提供します。 実装は非常に原始的であり、ソリューションと直接的な関係はありません。

bmCreate :: Int -> BitMask bmLength :: BitMask -> Int bmSize :: BitMask -> Int bmIsEmpty :: BitMask -> Bool bmNot :: BitMask -> BitMask bmAnd :: BitMask -> BitMask -> BitMask bmOr :: BitMask -> BitMask -> BitMask bmIntersection :: [BitMask] -> BitMask bmUnion :: [BitMask] -> BitMask bmSplit :: BitMask -> [BitMask] bmByOne :: BitMask -> [BitMask] bmExpand :: BitMask -> BitMask bmFillGaps :: BitMask -> BitMask bmLeftIncursion :: Int -> BitMask -> BitMask bmRightIncursion :: Int -> BitMask -> BitMask bmTranspose :: [BitMask] -> [BitMask]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

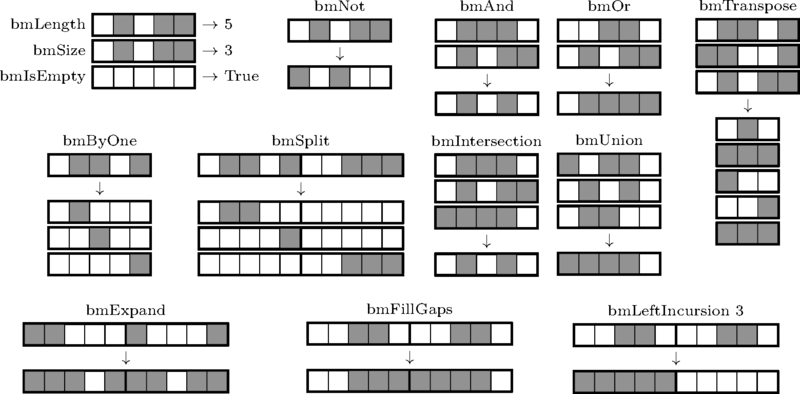
このようなグラフィカルな記述は、おそらくbmLeftIncursion



とbmRightIncursion



を除くすべての機能を網羅しているとbmRightIncursion



ます。 それらが必要な理由は後で明らかになりますが、その動作の原理は次のとおりです： bmLeftIncursion



は左端のビットを検出し、すべてのビットがその前に埋められるマスクと、関数が呼び出されたときに指定されたビットで始まるビットを作成します; 2番目の関数も同様に機能します。

構造

クロスワードの解は線に沿って発生するため、フィールド全体に対応するタイプはすべての水平線と垂直線のセットですが、これはクロスワードのすべてのセルの複製につながります。

 data Field = Field { flHorLines :: [Line], flVerLines :: [Line] } deriving Eq
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

各行には、セルとブロックに関する情報が保存されます（ブロックは条件の番号に対応します）。

 data Line = Line { lnMask :: LineMask, lnBlocks :: [Block] } deriving Eq
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

セルに関する情報は、同じ長さの2つのビットマスクの形式で保存され、塗りつぶされたセルとブロックされたセルを表します。

 data LineMask = LineMask { lmFilledMask :: BitMask, lmBlockedMask :: BitMask } deriving Eq
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ブロックには、番号自体に加えて、このブロックが存在できる行の領域に対応するマスクが含まれています。

 data Block = Block { blScopeMask :: BitMask, blNumber :: Int } deriving Eq
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ソリューションの開始時には、塗りつぶされたセルとブロックされたセルのマスクは空になり、ブロックのマスクは逆に完全に塗りつぶされます。 これは、すべてのセルが空であり、各ブロックが行のどの部分にあってもよいことを意味します。 解決プロセスは、各ブロックの面積をその数に等しいサイズに狭め、それに応じてマスクを埋めることになります。

完了と同期

上記のすべてのタイプ（ BitMask



を除く）は、 Completable



とSyncable



2つのクラスのインスタンスです。



Completable



クラスの唯一の機能は、オブジェクトの「完全性」を示します。 すべての行が完了している場合、フィールドは完了したと見なされます。 すべてのブロックが完了すると、ラインが完成します。 同時に、不必要にマスクを完成する必要があります（ブロックの完全性に起因します。なぜか、もう少し後で明らかになります）。 前述のように、ブロックを完了するには、その領域のサイズがその番号と一致する必要があります。

 class Completable a where clIsCompleted :: a -> Bool instance Completable Field where clIsCompleted fl = all clIsCompleted (flHorLines fl) && all clIsCompleted (flVerLines fl) instance Completable Line where clIsCompleted ln = all clIsCompleted (lnBlocks ln) instance Completable Block where clIsCompleted bl = bmSize (blScopeMask bl) == blNumber bl
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Syncable



クラスは、さまざまな決定ブランチをまとめることができる関数を提供します。 snAverage



は、2つのブランチから一般のみを抽出し、 snSync



少なくとも1つのブランチに出現したものをbmOr



bmAnd



およびbmOr



一般化をそれぞれ考慮することができます）。 snAverageAll



とsnSyncAll



はまったく同じことを行いますが、2つのオブジェクトではなく、オブジェクトのリストで機能します。

 class Syncable a where snSync :: a -> a -> Maybe a sn1 `snSync` sn2 = snSyncAll [sn1, sn2] snAverage :: a -> a -> Maybe a sn1 `snAverage` sn2 = snAverageAll [sn1, sn2] snSyncAll :: [a] -> Maybe a snSyncAll [] = Nothing snSyncAll sns = foldr1 (wrap snSync) (map return sns) snAverageAll :: [a] -> Maybe a snAverageAll [] = Nothing snAverageAll sns = foldr1 (wrap snAverage) (map return sns) wrap :: Monad m => (a -> b -> mc) -> ma -> mb -> mc wrap f mx my = do x <- mx y <- my fxy
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

コヒーレンス

Syncable



クラスの関数の説明から、それらの結果はMaybe



モナドにラップされたオブジェクトSyncable



ことがSyncable



ます。 実際、これは一貫性の重要な概念がどのように現れるかであり、上記のすべてのタイプにも定義されていますが、カプセル化の理由で別のクラスに移動されていません。 例として、同じセルを同時にシェーディングしてロックすることはできません。 操作がそのような状況につながる可能性がある場合は、 Maybe



モナド（通常はtype TransformFunction a = a -> Maybe a



）でマークされ、この状況につながる場合、結果はNothing



になります。プログラム内のオブジェクトが矛盾した状態で存在することはできません。 また、 Nothing



は他のオブジェクトの不可欠な部分にはなれないため、フィールド全体が調整されなくなり、ソリューションが存在しなくなります。



水平線と垂直線の同期により、フィールドの一貫性が確保されます。 したがって、セルが水平線のある状態（塗りつぶし、ブロック、または空）にある場合、対応する垂直線のセルはまったく同じ状態になり、その逆も同様です。

 flEnsureConsistency :: TransformFunction Field flEnsureConsistency fl = do let lnsHor = flHorLines fl let lnsVer = flVerLines fl lnsHor' <- zipWithM lnSyncWithLineMask (lmTranspose $ map lnMask lnsVer) lnsHor lnsVer' <- zipWithM lnSyncWithLineMask (lmTranspose $ map lnMask lnsHor) lnsVer return $ Field lnsHor' lnsVer' lnSyncWithLineMask :: LineMask -> TransformFunction Line lnSyncWithLineMask lm ln = do lm' <- lm `snSync` lnMask ln return ln { lnMask = lm' }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ラインの一貫性については、決定プロセスに直接関係するため、後で説明します。



ブロックの一貫性は非自明に提供されます。そのため、ブロック領域から、それを収容できない連続部分を除外する必要があります。 したがって、番号3のブロック領域と元の領域から マスクを除外 （たとえば、このセルがブロックされたという事実のため）、この操作の最終結果はエリアのあるブロックになります でも全然 。

 blEnsureConsistency :: TransformFunction Block blEnsureConsistency bl = do let bms = filter ((blNumber bl <=) . bmSize) $ bmSplit $ blScopeMask bl guard $ not $ null bms return bl { blScopeMask = bmUnion bms }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

マスクの場合、一貫性は明らかであり、すでに上で説明されています。同じセルを同時にペイントしてブロックすることはできません。

 lmEnsureConsistency :: TransformFunction LineMask lmEnsureConsistency lm = do guard $ bmIsEmpty $ lmFilledMask lm `bmAnd` lmBlockedMask lm return lm
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

コンバージョン数

マスクとブロックを変換する操作は非常に限られています。セルを解決するプロセスでは、塗りつぶしてブロックすることしかできず（心を変えて消しゴムを消して消すことはできません）、ブロック領域は狭めることができるだけです。

 lmFill :: BitMask -> TransformFunction LineMask lmFill bm lm = lmEnsureConsistency lm { lmFilledMask = lmFilledMask lm `bmOr` bm } lmBlock :: BitMask -> TransformFunction LineMask lmBlock bm lm = lmEnsureConsistency lm { lmBlockedMask = lmBlockedMask lm `bmOr` bm } blExclude :: BitMask -> TransformFunction Block blExclude bm bl = blEnsureConsistency $ bl { blScopeMask = blScopeMask bl `bmAnd` bmNot bm } blKeep :: BitMask -> TransformFunction Block blKeep bm bl = blEnsureConsistency $ bl { blScopeMask = blScopeMask bl `bmAnd` bm }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

解決策

最終的に全体像を形成するまで、決定プロセスは別々の部分で検討されます。

行の一貫性

最初に、一貫性に関するセクションに残ったギャップを復元し、ブロックに従ってマスクが塗りつぶされた場合に行が一貫していると見なされることを宣言します。 このフレーズの背後には2つのポイントが隠れています。 まず、どのブロックの領域にも該当しないセルをブロックする必要があります（行にブロックが含まれていない場合、それに応じてすべてのセルがブロックされます）。

 lnUpdateBlocked :: [Block] -> TransformFunction LineMask lnUpdateBlocked [] lm = lmBlock (bmNot $ lmBlockedMask lm) lm lnUpdateBlocked bls lm = lmBlock (bmNot $ bmUnion $ map blScopeMask bls) lm
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、各ブロックに対して、 blToFillMask



関数を使用して、ペイントする必要があるマスクを取得できます。 ブロックをエリアの左右に「ドライブ」すると、2つのマスクが交差します。

 blMinimumLeftMask :: Block -> BitMask blMinimumLeftMask bl = bmLeftIncursion (blNumber bl) (blScopeMask bl) blMinimumRightMask :: Block -> BitMask blMinimumRightMask bl = bmRightIncursion (blNumber bl) (blScopeMask bl) blToFillMask :: Block -> BitMask blToFillMask bl = blMinimumLeftMask bl `bmAnd` blMinimumRightMask bl lnUpdateFilled :: [Block] -> TransformFunction LineMask lnUpdateFilled [] = return lnUpdateFilled bls = lmFill (bmUnion $ map blToFillMask bls)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

（注：ここで、最終的にbmLeftIncursion



およびbmRightIncursion



使用しbmLeftIncursion



。厳密に言えば、 bmRightIncursion



がこの目的にのみ使用された場合、おそらく少し異なるように見えます。つまり、最初のビットが満たされるまでビットマスクを埋めませんソースマスク。）



したがって、前述のように、ラインの一貫性条件により、すべてのブロックが完了した場合にマスクが常に完了することが保証されます。

 lnEnsureConsistency :: TransformFunction Line lnEnsureConsistency ln = do let bls = lnBlocks ln lm <- lnUpdateBlocked bls >=> lnUpdateFilled bls $ lnMask ln return $ ln { lnMask = lm }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

シンプルなライン変換

ライン内の決定は、本質的に2つの変換に要約されます。



実際、最初の変換は一貫性条件の逆です。つまり、マスクが完了すると、ブロックが完了します。 これには3つのアクションが使用されます。

1. すべてのブロックされたセルは、すべてのブロックの領域から除外する必要があります。
   
   
   
   

    lnRemoveBlocked :: LineMask -> TransformFunction [Block] lnRemoveBlocked = mapM . blExclude . lmBlockedMask
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
2. ブロックがマスクの連続した影の部分に対応できない場合（つまり、ブロック領域からはみ出ているか、サイズよりもサイズが大きい場合）、ブロック領域から除外する必要があります。
   
   
   
   

    lnRemoveFilled :: LineMask -> TransformFunction [Block] lnRemoveFilled lm = mapM (\ bl -> foldM f bl $ bmSplit $ lmFilledMask lm) where f bl bm = if blCanContainMask bm bl then return bl else blExclude (bmExpand bm) bl blCanContainMask :: BitMask -> Block -> Bool blCanContainMask bm bl = let bm' = bmFillGaps bm in bmSize bm' <= blNumber bl && bmIsEmpty (bm' `bmAnd` bmNot (blScopeMask bl))
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
3. blMinimumLeftMask
   
   
   
   右隣のblMinimumRightMask
   
   
   
   各ブロックの領域から除外する必要があります（ここでは、上記の形式で正確に必要です）。 正確には、ブロック間に少なくとも1つの空のセルが存在する必要があるため、1つのセルで展開されたこれらのマスクは除外されます。
   
   
   
   

    lnExcludeNeighbours :: TransformFunction [Block] lnExcludeNeighbours bls = sequence $ scanr1 (flip $ wrap $ blExclude . bmExpand . blMinimumRightMask) $ scanl1 (wrap $ blExclude . bmExpand . blMinimumLeftMask) $ map return bls
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   

これらのアクションが一緒になって、次の関数を形成します（ slLoop



関数については後述します）。

 lnSimpleTransform :: TransformFunction Line lnSimpleTransform ln = do let lm = lnMask ln bls <- lnRemoveBlocked lm >=> slLoop (lnRemoveFilled lm >=> lnExcludeNeighbours) $ lnBlocks ln lnEnsureConsistency ln { lnBlocks = bls }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2行目の変換

原則としてマスクの影付き部分を含むことができるすべてのブロックの左端を取得すると、その右端の位置はこのマスク自体に制限されます。これがさらに右に移動すると、この影付きの領域は誰にも「与えられない」からです。 これらのブロックの右端にも同じ考慮事項が当てはまります。

 lnExtremeOwners :: BitMask -> TransformFunction [Block] lnExtremeOwners bm bls = do bls' <- fmap reverse $ maybe (return bls) (f bmLeftIncursion bls) (h bls) fmap reverse $ maybe (return bls') (f bmRightIncursion bls') (h bls') where fg = varyNth (\ bl -> blKeep (g (blNumber bl) bm) bl) h = findIndex (blCanContainMask bm) varyNth :: Monad m => (a -> ma) -> [a] -> Int -> m [a] varyNth f xs idx = do let (xs1, x : xs2) = splitAt idx xs x' <- fx return $ xs1 ++ x' : xs2
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この推論をマスクの各連続部分に適用すると、2行目の変換が得られます。

 lnTransformByExtremeOwners :: TransformFunction Line lnTransformByExtremeOwners ln = do bls <- foldM (flip lnExtremeOwners) (lnBlocks ln) $ bmSplit $ lmFilledMask $ lnMask ln lnEnsureConsistency ln { lnBlocks = bls }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

フィールド変換

フィールドにはそれ自体の特別な変換はありません;唯一のオプションは、既製の変換を行い、それをすべての行に適用することです。

 flTransformByLines :: TransformFunction Line -> TransformFunction Field flTransformByLines f fl = do lnsHor <- mapM f (flHorLines fl) fl' <- flEnsureConsistency fl { flHorLines = lnsHor } lnsVer <- mapM f (flVerLines fl') flEnsureConsistency fl' { flVerLines = lnsVer }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

枝

日本語のクロスワードを解くのはNP完全なタスクであるため、分岐せずに行うことはできません。 type ForkFunction a = a -> [[a]]



型の関数として分岐を定義します。内部リストには相互に排他的なオプションが含まれ、外部リストにはこれらのオプションを生成するさまざまな方法が含まれます。



最も単純な方法は、セルに分岐することです。各空のセルは、外部リストの1つの要素を生成します。これは、2つの要素のリストであり、一方のセルはもう一方のセルで埋められます。

 lnForkByCells :: ForkFunction Line lnForkByCells ln = do let lm = lnMask ln bm <- bmByOne $ lmEmptyMask lm return $ do lm' <- [fromJust $ lmBlock bm lm, fromJust $ lmFill bm lm] maybeToList $ lnEnsureConsistency ln { lnMask = lm' } flForkByCells :: ForkFunction Field flForkByCells fl = do let lnsHor = flHorLines fl let lnsVer = flVerLines fl idx <- findIndices (not . clIsCompleted) lnsHor let (lns1, ln : lns2) = splitAt idx lnsHor lns <- lnForkByCells ln return $ do ln' <- lns maybeToList $ flEnsureConsistency $ Field (lns1 ++ ln' : lns2) lnsVer
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

別の分岐方法もラインで使用できます。マスクの連続した影付きの部分（外部リスト）ごとに、ブランチを定義するオプションとして、それを含むことができるブロックのセット（内部リスト）を検討できます。

 lnForkByOwners :: ForkFunction Line lnForkByOwners ln = do let bls = lnBlocks ln bm <- bmSplit $ lmFilledMask $ lnMask ln case findIndices (blCanContainMask bm) bls of [_] -> [] idxs -> return $ do idx <- idxs maybeToList $ do bls' <- varyNth (g bm) bls idx lnEnsureConsistency ln { lnBlocks = bls' } where g bm bl = blKeep ((bmAnd `on` ($ bm) . ($ blNumber bl)) bmLeftIncursion bmRightIncursion) bl
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

一般化された関数

ほとんどの変換を繰り返し適用することは理にかなっています。 この場合、少なくとも何かが変更されるまで変換を単純に適用するか、不必要な適用にかなりの時間がかかる場合は、オブジェクトの完全性を事前にチェックすることができます。

 slLoop :: Eq a => TransformFunction a -> TransformFunction a slLoop fx = do x' <- fx if x == x' then return x else slLoop fx' slSmartLoop :: (Completable a, Eq a) => TransformFunction a -> TransformFunction a slSmartLoop fx | clIsCompleted x = return x | otherwise = do x' <- fx if x == x' then return x else slLoop fx'
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

分岐結果は、特定のデータ型と分岐方法に関係なく処理できます。 これを行うには、特定の分岐方法を適用し、結果の各オブジェクトに何らかの変換を適用するには、相互に排他的な分岐の各セットの平均値を取得し、異なる分岐点で取得したこれらの平均オブジェクトを同期する必要があります。 詳細については説明しませんが、この操作では、完全性のチェックに関連する最適化バージョンも利用できます。

 slForkAndSyncAll :: (Syncable a) => ForkFunction a -> TransformFunction a -> TransformFunction a slForkAndSyncAll fgx = do xs <- mapM (snAverageAll . mapMaybe g) $ fx snSyncAll (x : xs) slForkAndSmartSync :: (Syncable a, Completable a, Eq a) => ForkFunction a -> TransformFunction a -> TransformFunction a slForkAndSmartSync fgx = foldr h (return x) (fx) where h xs mx = do x' <- mx if clIsCompleted x' then mx else case mapMaybe (snSync x') xs of [] -> Nothing xs' -> case filter (/= x') xs' of [] -> return x' xs'' -> snAverageAll . mapMaybe g $ xs''
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最後に、他のすべてが失敗した場合、再帰に進むことができます。 複数のソリューションがある場合、この方法でのみすべてのソリューションを取得できます。

 slAllSolutions :: (Completable a) => ForkFunction a -> TransformFunction a -> a -> [a] slAllSolutions fgx = do x' <- maybeToList $ gx if clIsCompleted x' then return x' else case fx' of (xs : _) -> do x'' <- xs slAllSolutions fg x'' [] -> []
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

フィン・ベンコ

それだけです 使用可能なツールは、いくつかの簡単な手順でソルバーを取得するのに十分です。

1. 2つのライン変換を組み合わせます。
   
   
   
   

    lineTransform = slSmartLoop $ lnSimpleTransform >=> lnTransformByExtremeOwners
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
2. 行固有の分岐を処理します。
   
   
   
   

    lineTransform' = slForkAndSyncAll lnForkByOwners lineTransform
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
3. これら2つの変換からフィールド変換を作成します。
   
   
   
   

    fieldTransform = slSmartLoop $ slSmartLoop (flTransformByLines lineTransform) >=> flTransformByLines lineTransform'
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
4. フィールドをセルに分岐した結果を処理します。
   
   
   
   

    fieldTransform' = slForkAndSmartSync flForkByCells fieldTransform
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
5. 前の2つの変換を組み合わせます。
   
   
   
   

    fieldTransform'' = slSmartLoop $ fieldTransform >=> fieldTransform'
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   
6. そして最後に、再帰を追加します。
   
   
   
   

    solve = slAllSolutions flForkByCells fieldTransform''
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   

あとがき

このプログラムは、単一のソリューションを備えたクロスワードで非常に高速に実行されます。ラップトップにある数千のクロスワードのうち、2つ（序文で作成されたものを含む）だけが1分以上解決され、ほとんどすべてが10秒で収まり、それらのいずれも再帰を必要としませんでした。



理論的には、いくつかの改良を加えて、プログラムを使用してクロスワードの複雑さを自動的に評価し（ソリューションの方法は一般に人が使用する方法と似ているため）、ソリューションの一意性を証明できます。 LaTeXへのエクスポートが利用可能であり、SVNにもすぐに登場するかもしれません。 だから、あなたが望むなら、あなたは雑誌の家の問題を整理することができます:)