実際の最適化自体については以下で説明します(「外接円の方程式によるドローネ条件のチェックのアルゴリズムの最適化」を参照)が、すべてについて順番に説明します。
私の場合、イメージトレーシングでは、平面をプリミティブセクター(三角形)に分割するために三角形分割が使用されます。 ご存知のように、調整、境界の識別、境界のバイパス、輪郭のスイープなど、いくつかの段階に分けられます。 これは最も一般的な形式です。 私は、最も困難な段階、つまり飛行機を掃除する段階で停止したいと思います。
入り口で
出力で境界線を検出してトラバースした後、多くの外部輪郭が得られました。 各輪郭の輪郭には異なる色が付いています。 既知の各回路には、既知の数の内部回路も含まれています。
したがって、「平面を掃除する」という観点から、外部の輪郭を個別に考慮すると、多くのポイントがあり、各ポイントには左右に1つの隣接点があります。 つまり すべてのポイントはチェーンで閉じられ、単一の「ぶら下がり」ポイントはなく、各チェーンには少なくとも3つのポイントが含まれます(図1)。
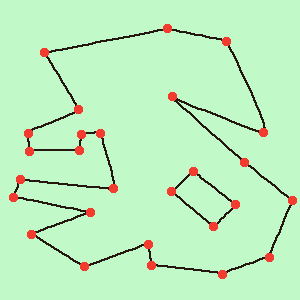
図1
どうする
図を三角形でスイープする必要があります。
検索
本[1]を読んだ後、少なくとも何らかの形で私のケースに適したDelaunay三角形分割を構築する単一の(少なくとも1つの)方法が見つかりませんでした。 他の本を検索しませんでした。 はい、これで十分でした。彼女は私の頭の考えを整理してくれました。 その結果、彼は「自転車」を発明しました。
アルゴリズム
1)まず最初に、検討中の図にはシーケンスが1つしかないと仮定します。 それからすべては、三角形の連続的な撤回に帰着します。 任意の点を取り、隣接する点で三角形を構築しようとします。 三角形を構築できなかった場合(これら2つの点を結ぶ線が既に構築されたものと交差するか、線が除外ゾーンを通過する場合(図2))、次の点に移動します。作成元のポイントを削除します(図4)。

図2
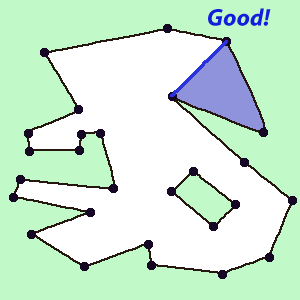
図3

図4
もう1つ:次の三角形を保存するときは、頂点を時計回りに(正しい座標系で)記録する必要があります。 これは将来、コンピューティングリソースを削減するのに役立ちます。
2)平面全体をスイープするまで手順1を繰り返します。
3)複数のシーケンスがある場合、つまり 1つ、およびその内部に1つ以上の内部輪郭(図1)。 ここでは、各シーケンスを個別に考慮する必要があります。 次の内側の輪郭を取ります。 1つの外部と1つの内部から、2つの単一回路を作成します。 これを行うには、1つの回路から別の回路への2つの「ポート」を見つけます。 「ポート」の条件:それらは互いに交差してはならず(端に触れないこと)、等高線と交差してはなりません(図5)。

図5
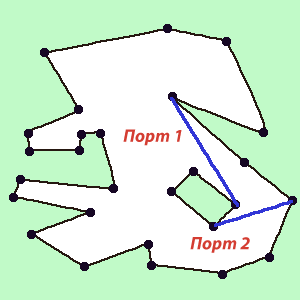
図6
4)次に、すべての内部シーケンスを、互いに分離された、すでに形成された(パラグラフ3)シーケンスに順番に導入する必要があります。 新しいものを含むものとマージする必要があります。 定義上、内部シーケンスは他のものと接触したり交差したりすることはなく(1つの外部とすべての可能な内部の両方)、すべてがスムーズに進みます。
ポートを見つけたら(図6)、新しいシーケンスを構築し、現在のアルゴリズムのポイント1と2でそれらをバイパスするのは簡単です(図7)。
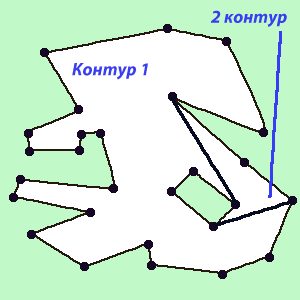
図7
5)第4段階の後、三角形のリストが表示されます(図8)。 彼らはすでにタスクを完了したかのように見えますが、写真を美しくするために残っています。ドローネ条件が満たされていることを確認してください(図9)。
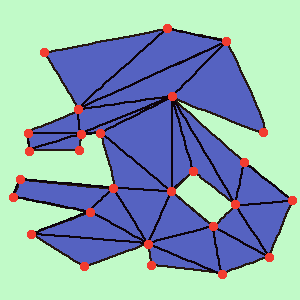
図8
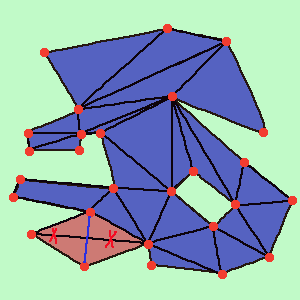
図9
6)6つ目のポイントについてお話しします。 これは、アイテム番号5で受け取った三角形のリストを順番に実行します。 まず、すべての三角形に「ダーティ」というラベルを付けます。 各サイクルで、各三角形のドロネー条件をチェックします。 条件が満たされない場合は、再構築を行い、隣人と現在の三角形を「ダーティ」としてマークします。 条件が満たされている場合は、クリーンとしてマークします。 アルゴリズムの私の実装では、各三角形はその隣接への参照を持っています。 この場合、6番目のアイテムが最速です。
5番目のステージの詳細をご覧ください。
さて、私の知る限り、三角形がドロネー条件を満たしているかどうかを判断する方法は2つあります。1)反対の角度の合計を確認します。 180未満でなければなりません。2)外接円の中心を計算し、4番目の点までの距離を計算します。 ポイントが外接円の外側にある場合、ドロネー条件が満たされていることを誰もが知っています。
計算の力No. 1:乗算/除算の10の演算と加算/減算の13の演算。
計算の力No. 2:乗算/除算の29演算と加算/減算の24演算。
例えば本[1]で計算されている計算能力の観点から、オプションNo. 1はより収益性が高い。 そうでない場合は、彼はそれを実現しました(図10)。 この方法を「コンベヤ」に設定した後に判明したように、結果として生じる不確実性。 これは、角度A自体が180度を超える場合のオプションです。 本[1]では、個別のプライベートメソッドの1つとして考えられています。 そして、そのすべての優雅さ、透明性、パフォーマンスは消えます。 また、後に、方法2を非常に大幅に最適化できることが判明しました。
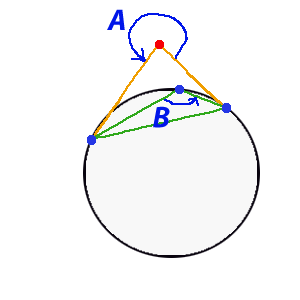
図10
外接円の方程式を通してドローネ条件をチェックするためのアルゴリズムの最適化
次は純粋な数学です。
だから私たちは持っています:
点M(X、Y)の条件を、点A(x1、y1)、B(x2、y2)、C(x3、y3)を通る円の方程式で確認するには、次の形式で記述できます。
(a⋅(X ^ 2 + Y ^ 2)-b⋅X + c⋅Y-d)⋅sign a≥0
詳細は壮大な本[1]に記載されています。 (いいえ、私は彼女の著者ではありません)
したがって、符号aはバイパス方向の符号であり、最初から時計回りに三角形を作成したため、省略できます(1に等しい)。
次に、座標の中心をポイントMに移動すると、次の結果が得られます(図11)。
A(x1-X、y1-Y)、B(x2-X、y2-Y)、B(x3-X、y3-Y);
-d> = 0
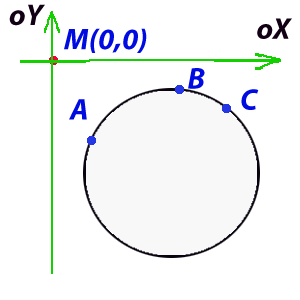
図11
それだけじゃない?
d <= 0
本によると、再び、[1]
(x1^2 + y1^2)*(y2*x3 - x2*y3) + (x2^2 + y2^2)*(x1*y3 - y1*x3) + (x3^2 + y3^2)*(y1*x2 - x1*y2) <= 0
乗算/除算の15演算と加算/減算の14演算があります。
ご清聴ありがとうございました。 批判を待っています。
使用された文献のリスト
1. Skvortsov A.V. ドローネの三角形分割とその応用。 -トムスク:出版社トム。 大学、2002年-128秒 ISBN 5-7511-1501-5