生データ処理
したがって、12次元データの配列がいくつかあり、13番目のバイナリフィールドを予測するためのモデルを作成する必要がありました。 これは分類タスクです。 通常の分析は、分類器への前処理を行わずにアレイ全体を駆動し(ニューラルネットワークを使用)、災害の規模を評価するために結果を確認することから始まります。 これによりめったに良い結果が得られることはめったにありませんが、すべてがどれほど悪いかを一般的に理解することができます。 結果が最良ではなかったことに驚かなかったので、分析の次のステップに進みます。
可視化
視覚化により、データを視覚的に評価できます。たとえば、データが複数のグループを形成していることを確認でき、その後、クラスターごとに分類器をトレーニングできます。 クラスタリングの結果によれば、最初の分類器はいくつかのクラス(クラスタリングアルゴリズムによって検出されるクラスター)に組み込まれ、その後、各クラス/クラスターはターゲットフィールドに独自の分類器を使用します。 知っているように、k-meansアルゴリズムは入力としてクラスターの数を受け入れ、データを指定された数のグループに分割します。 クラスターの数を並べ替えて最小コストのパーティションを探す代わりに、データを視覚化してこれらのグループを表示できます。 しかし、別の問題もあります。たとえば、データをユークリッド距離で除算すると、非常に暗黙的なクラスター境界が得られ、それらは互いに非常に近くなり、システム全体の精度が低下します。
ですから、私はレンダリングを始めていますが、12次元のスペースをレンダリングするのはそれほど簡単ではないので、ディメンションを3または2に減らす必要があります。 簡単です。 次元を縮小するために、私はlastの前の記事で説明されたまさにその実装方法によって、 主成分のメソッドを使用します。
その結果、私はこの写真を得ました:
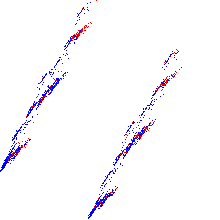
青と赤のドットは、ターゲットフィールドによって形成される2つのクラスです。
クラスタリング
上の図は、データ投影が明確な境界を持つ明確な2つのグループを形成することを示しています。 ここで、パラメーター2を使用してk-meansクラスタリングを行う必要があります。しかし、ここで問題となります。これに使用するメトリック。 ユークリッドメトリックはラウンドガウス分布を作成します(正確にはガウス分布であるため、前の記事に関する私のコメントを読むことができます)が、肉眼で見ても、クラスターの周りの円を記述すると交差します。
ユークリッドメトリックによるクラスタリングは次のようになります。

境界は非常にぼやけており、実際、クラスターは私たちが望んでいたものとは完全に異なっていることが判明しました。
マハラノビス距離を使用したクラスタリングは楕円ガウス分布を構築します。最初の図では、クラスターの周りに記述された2つの互いに素な楕円を精神的に描くのは非常に簡単です。
このようなクラスタリングの結果は次のとおりです。

利益
利益があるかどうかはまだ明確ではありませんが、クラスタリングによって2つの異なるデータグループが得られ、モデルの最初の段階を構築できるようになりました。 または、各クラスターを個別のタスクとして使用します。 さらに、各グループに対して、ターゲットフィールドによる分類子がトレーニングされます。ただし、これはこの記事のフレームワーク内ではなくなります-)