少し科学的な調査を行った後(つまり、サイトで検索したところ)、ハブにはタグ計算ジオメトリを備えた記事が2つしかなく、そのうちの1つが私のものであることがわかりました。 なぜなら 最近、私はこのトピックにいくらか興味を持ち、いわゆる最小凸包の構築の問題を考慮することにより、アルゴリズム幾何学のトピックを続けることにしました。 右の図は、鋭い鷹の読者にそれが何であるかを徹底的に説明していますが、それにもかかわらず、カットの下でもう少し正式な定義が与えられ、最小凸包を構築するための2つの古典的なアルゴリズムが説明されます。
最小凸包の概念
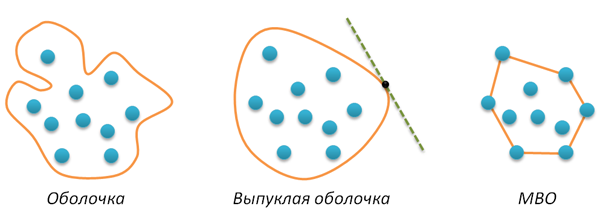
平面上の点Aの有限集合を与えてみましょう。この集合のシェルは 、Aからのすべての点がこの曲線の内側にあるような自己交差のない閉じた線Hです。 曲線Hが凸である場合(たとえば、この曲線の接線が他の点で交差しない場合)、対応するハルは凸と呼ばれます。 最後に、 最小凸包 (以下、MBOと略します)は、最小長(最小周囲長)の凸包です。 私はチェックしませんでした(これは矛盾によって証明できるようです)が、最小シェルが単純に凸でなければならないことは明らかです。 導入されたすべての概念を次の図に示します。
ポイントセットAのMBOの主な特徴は、このシェルが頂点がAのいくつかのポイントである凸多角形であるということです。したがって、MBOを見つける問題は最終的にAから必要なポイントを選択および順序付けすることになります。アルゴリズムの出力は多角形、つまり 頂点のシーケンス。 さらに、頂点の順序に条件を課します—ポリゴントラバースの方向は正でなければなりません(図は反時計回りに正としてトラバースされることを思い出します)。
MBOを構築するタスクは、計算幾何学の最も単純な問題の1つと考えられています;それには多くの異なるアルゴリズムがあります。 以下では、グラハムスキャンとジャービスマーチの2つのアルゴリズムを検討します。 それらの説明はPythonコードで示されています。 両方のアルゴリズムには、前の投稿で詳しく説明した回転機能が必要です。 この関数は、ポイントABがベクトルABのどちら側に位置するかを決定します(正の戻り値は左側に対応し、負の値は右側に対応します)。
def rotate(A,B,C): return (B[0]-A[0])*(C[1]-B[1])-(B[1]-A[1])*(C[0]-B[0])
グラハムのアルゴリズム(グラハムスキャン)
このアルゴリズムは3ステップです。 最初のステップで、MBOに含まれることが保証されているAの任意のポイントが検索されます。 このようなポイントは、たとえば、x座標が最小のポイント(Aの左端のポイント)であることが簡単にわかります。 このポイント(開始ポイントと呼びます)をリストの一番上に移動し、残りのポイントですべての作業を行います。 何らかの理由で、ポイントAの初期配列は変更されません。ポイントを使用するすべての操作に間接アドレス指定を使用します。ポイントの数が格納されるリストPを作成します(配列Aの位置)。 したがって、アルゴリズムの最初のステップは、Pの最初のポイントを最小のx座標を持つポイントにすることです。 コード:
def grahamscan(A): n = len(A) # P = range(n) # for i in range(1,n): if A[P[i]][0]<A[P[0]][0]: # P[i]- P[0]- P[i], P[0] = P[0], P[i] #
グラハムアルゴリズムの2番目のステップは、すべてのポイント(P [0]番目を除く)を、開始ポイントR = A P [0]を基準にしたレフトリズムの度合いでソートすることです。 点CがベクトルRBの左側にある場合、B <Cと言います。

このような順序付けを実行するには、要素のペアごとの比較に基づく並べ替えアルゴリズム(クイック並べ替えなど)を使用できます。 何らかの理由で(主なものは不器用*手です)、挿入ソートを使用します。
* この場合に組み込みのPythonソートを適用する方法を説明できる人には非常に感謝します...
したがって、挿入によるソート(間接アドレス指定とゼロ点がソートされないことを忘れないでください):
for i in range(2,n): j = i while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0): P[j], P[j-1] = P[j-1], P[j] j -= 1
ソートの結果は、次の図で説明できます。
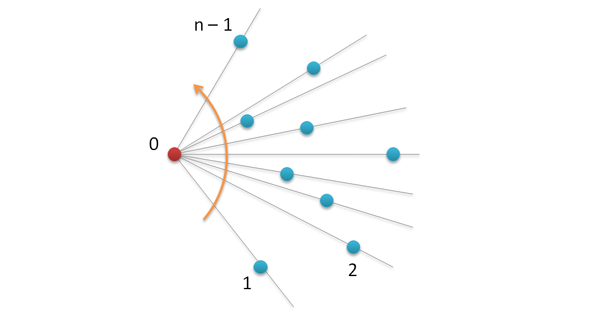
この順序でポイントを接続すると、多角形が得られますが、これは凸ではありません。
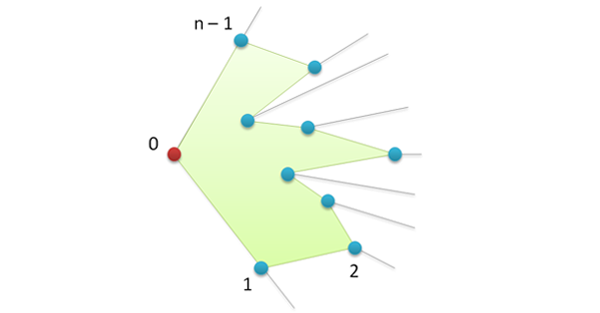
3番目のアクションに進みます。 私たちがしなければならないのは、角を切ることです。 これを行うには、すべての頂点を調べて、右旋回が実行される頂点を削除します(そのような頂点の角度は、展開された頂点よりも大きくなります)。 スタックS(実際にはリスト)を作成し、その上に最初の2つの頂点を配置します(これらは再び、MBOに含まれることが保証されます)。
S = [P[0],P[1]]
次に、他のすべての頂点に目を通し、Sスタックの最後の2つの頂点の視点からそれらの回転方向を追跡します。この方向が負の場合、スタックから最後の頂点を削除することで角度をカットできます。 ターンが正になるとすぐに、コーナーのカットが完了し、現在の頂点がスタックにプッシュされます。
for i in range(2,n): while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0: del S[-1] # pop(S) S.append(P[i]) # push(S,P[i])
その結果、スタックS(リストとして表示できるようになった)には、必要な方向の頂点のシーケンスが含まれ、さらに、指定されたポイントAのセットのMBOが決定されます。
return S
アルゴリズムの最初と最後のステップの複雑さはnで線形です(ただし、後者の場合、ネストされたループがありますが、このサイクル内の各頂点はスタックに1回だけプッシュされ、そこから1回だけ削除されます)。したがって、アルゴリズム全体の複雑さは2番目のステップで決定されます-ソート。これは、nが大きい場合に挿入ソートが最適なオプションではない理由です。 これをクイックソートに置き換えると、O(nlogn)アルゴリズムの全体的な複雑さが得られます。 この時間は改善できますか? アルゴリズムが(私たちのように)点のペアワイズ比較に基づいている場合、この推定は一般に改善されないことが証明されます。 この観点から、グラハムアルゴリズムが最適です。 それにもかかわらず、非常に優れた機能はありません-最終的にMBOに入る頂点の数(3、5、10、またはn)が問題にならないという意味で適応性がなく、常に線形対数になります。 Jarvisアルゴリズムはこのような適応性を備えており、順調に進めています。
完全なGrahamアルゴリズムコード
def grahamscan(A): n = len(A) # P = range(n) # for i in range(1,n): if A[P[i]][0]<A[P[0]][0]: # P[i]- P[0]- P[i], P[0] = P[0], P[i] # for i in range(2,n): # j = i while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0): P[j], P[j-1] = P[j-1], P[j] j -= 1 S = [P[0],P[1]] # for i in range(2,n): while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0: del S[-1] # pop(S) S.append(P[i]) # push(S,P[i]) return S
ジャービスアルゴリズム
ジャービスアルゴリズム(別名ラッピングアルゴリズム)は、グラハムアルゴリズムよりも概念的に単純です。 これは2ステップであり、ソートは必要ありません。 最初のステップはまったく同じです-MBOに含まれることが保証されている開始点が必要です。Aから左端の点を取得します。
def jarvismarch(A): n = len(A) P = range(n) for i in range(1,n): if A[P[i]][0]<A[P[0]][0]: P[i], P[0] = P[0], P[i]
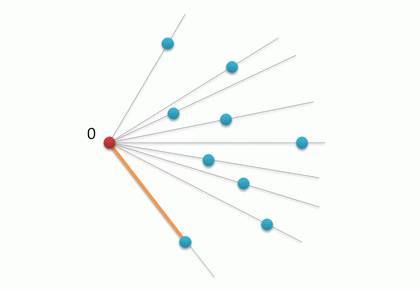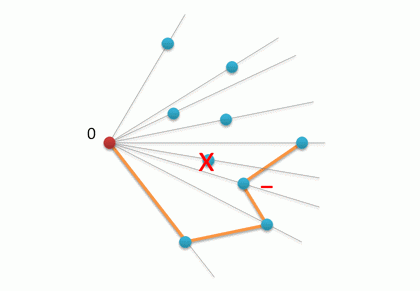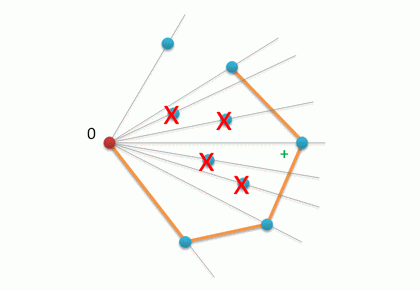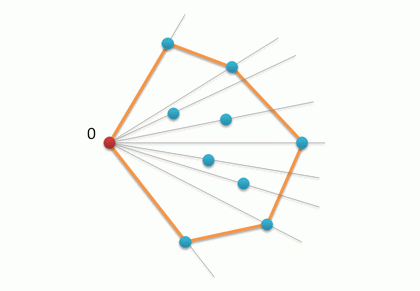
アルゴリズムの2番目のステップで、MBOが構築されます。 アイデア:開始頂点を現在にする、現在の頂点に対してAの右端の点を探す、現在の頂点にするなど。 プロセスは、開始頂点が再び現在の頂点になったときに終了します。 ポイントがMBOに達するとすぐに、それを考慮できなくなります。 したがって、MBOの頂点が正しい順序で格納される別のリストHがあります。 すぐにこのリストの開始頂点を入力し、リストPでこの頂点を最後に転送します(最終的にそこを見つけてアルゴリズムを完了します)。
H = [P[0]] del P[0] P.append(H[0])
ここで、無限ループを編成し、各反復で、Hの最後の頂点に対してPから左端の点を探します。この頂点が開始している場合は、サイクルを中断します。そうでない場合は、見つかった頂点をPからHに転送します。結果として返します。
while True: right = 0 for i in range(1,len(P)): if rotate(A[H[-1]],A[P[right]],A[P[i]])<0: right = i if P[right]==H[0]: break else: H.append(P[right]) del P[right] return H
うーん、私は写真を使わずにジャービスのアルゴリズムについて話すことができました。 次の図はすべてを示しています!

Jarvisアルゴリズムの複雑さを推定します。 最初のステップはnで線形です。 二番目はもっと面白いです。 ネストされたループがあり、外部反復の数はMBOの頂点の数hと等しく、内部反復の数はnを超えません。 したがって、アルゴリズム全体の複雑さはO(hn)です。 この式で珍しいのは、複雑さが入力データの長さだけでなく、出力の長さによっても決まることです(出力依存アルゴリズム)。 そして、
** タイムマシンは、一般的にアルゴリズムの観点から有用なものです。数兆年の計算を必要とするタスクは、ほぼ瞬時にその助けを借りて解決できます。プログラムを起動し、タイムマシンに入り、未来に「飛び」、結果を読んで、戻ってください。 数兆年の間、コンピューターの円滑な動作を確保する方法を理解することは残っています...
フルジャービスアルゴリズムコード
def jarvismarch(A): n = len(A) P = range(n) # start point for i in range(1,n): if A[P[i]][0]<A[P[0]][0]: P[i], P[0] = P[0], P[i] H = [P[0]] del P[0] P.append(H[0]) while True: right = 0 for i in range(1,len(P)): if rotate(A[H[-1]],A[P[right]],A[P[i]])<0: right = i if P[right]==H[0]: break else: H.append(P[right]) del P[right] return H
結論の代わりに
私の意見では、最小の凸包を構築するタスクは、計算幾何学のトピックに入るための良い方法であり、独自のアルゴリズムを考え出すのは非常に簡単です(ただし、Jarvisアルゴリズムのバリエーションになることは確かです)。 このタスクには多くのアプリケーションがあり、それらのほとんどはパターン認識、クラスタリングなどに関連していると主張されています。 さらに、MBOを構築するタスクは、計算ジオメトリのより複雑な問題を解決するための補助ツールとして使用されます。 はい、このタスクには非常に興味深い3次元の一般化があることに注意してください。
ご清聴ありがとうございました!