畳み込み行列
畳み込み行列を使用する多くのフィルターがあります;主なものは以下で説明されます。
畳み込み行列は、所望の結果を得るために画像ピクセルの値で「乗算」される係数の行列です。
以下は、畳み込み行列アプリケーションです。
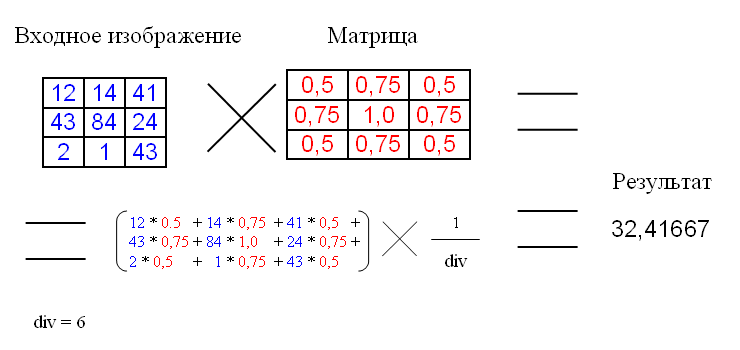
divは正規化係数であるため、平均強度は変化しません。
この例では、マトリックスのサイズは3x3ですが、サイズは大きくなる場合があります。
ぼかしフィルター
最も一般的に使用される畳み込み行列フィルターは、ぼかしフィルターです。
通常、行列は通常(ガウスの法則)に従って埋められます。 以下は、ガウス分布の法則に従って埋められた5x5のぼかし行列です。
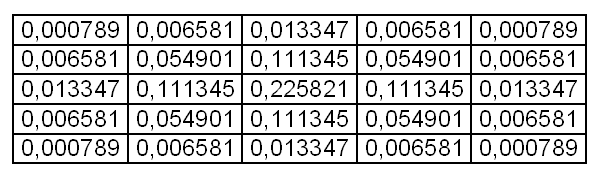
係数はすでに正規化されているため、この行列のdivは1です。
ぼかしの強さは、マトリックスのサイズに依存します。

境界条件に言及する価値があります(この問題はすべてのマトリックスフィルターに関連します)。 左上のピクセルの右側には「隣接」がないため、マトリックス係数を乗算するものは何もありません。
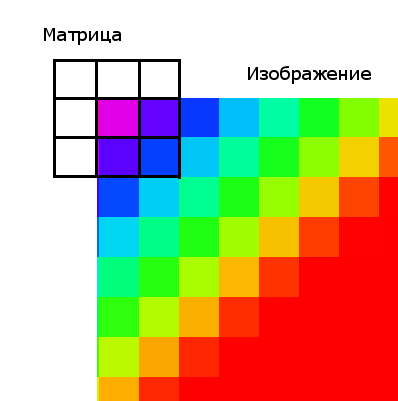
この問題には2つの解決策があります。
1.画像の「ウィンドウ」にのみフィルターを適用します。これは、左上隅の座標が[kernelSize / 2、kernelSize / 2]で、右下が[width-kernelSize / 2、height-kernelSize / 2]です。 kernelSize-行列サイズ。 幅、高さ-画像サイズ。
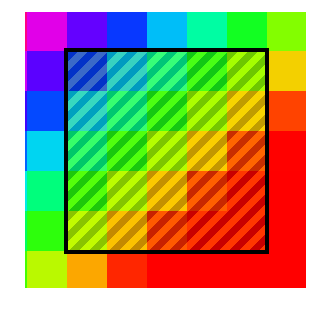
フィルタは画像全体に適用されないため、これは最良の方法ではありません。 同時に、フィルターサイズが大きい場合、品質はかなり低下します。
2. 2番目の方法(追加)では、中間イメージを作成する必要があります。 アイデアは、寸法(幅+ 2 * kernelSize / 2、高さ+ 2 * kernelSize / 2)で一時的なイメージを作成することです。 入力画像は画像の中央にコピーされ、エッジは画像の極端なピクセルで塗りつぶされます。 中間バッファにぼかしが適用され、結果がそこから抽出されます。

この方法には品質上の欠点はありませんが、不必要な計算を行う必要があります。
ガウスぼかしフィルターの複雑さはO(hi * wi * n * n)です。ここで、hi、wiは画像サイズ、nはマトリックス(フィルターコア)のサイズです。 このアルゴリズムは、許容可能な品質で最適化できます。
正方形のコア(マトリックス)は、水平と垂直の2つの1次元で置き換えることができます。 カーネルサイズ5の場合、次のようになります。

フィルターは2回のパスで適用されます。最初は水平方向、次に垂直方向(または回転ごと)の結果です。
このアルゴリズムの複雑さは、O(hi * wi * n)+ O(hi * wi * n)= 2 * O(hi * wi * n)になります。これは、カーネルサイズが2を超える場合、正方行列を使用した従来の方法よりも高速です。
明瞭フィルター
わかりやすくするために、次のマトリックスを使用する必要があります。
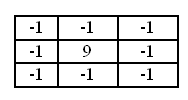
このマトリックスは、境界の値の差を大きくします。 この行列のDivは1です。

GIMPには「畳み込みマトリックス」フィルターがあり、必要なマトリックス変換の検索を簡素化します。
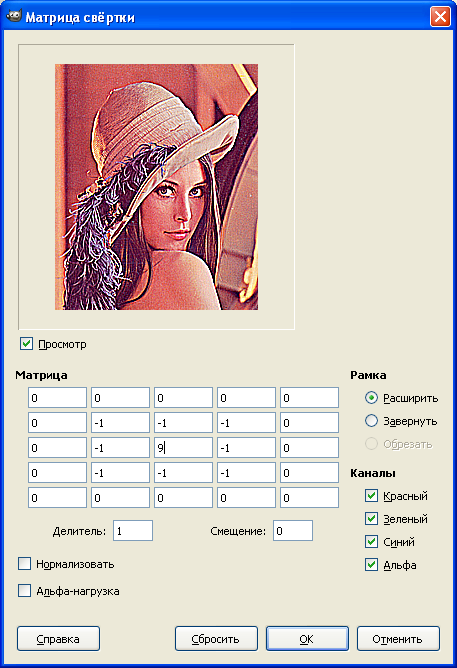
コンボリューションマトリックスに基づくフィルターの詳細については、記事「ねじれマトリックスに基づくグラフィックフィルター」を参照してください。
メディアンフィルター
メディアンフィルターは、一般的に、ノイズを減らす、または画像を「滑らかにする」ために使用されます。

フィルターはさまざまなサイズのマトリックスで機能しますが、畳み込みマトリックスとは異なり、マトリックスサイズは問題のピクセル数にのみ影響します。
メディアンフィルターアルゴリズムは次のとおりです。
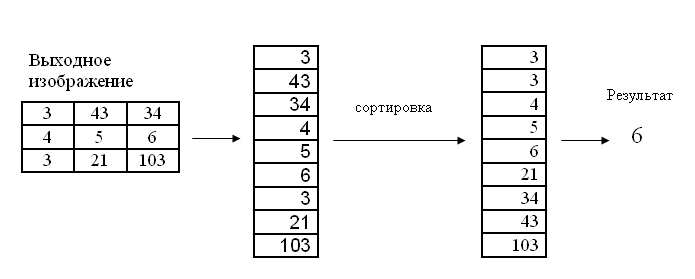
現在のピクセルでは、マトリックスに「落ちる」ピクセルがソートされ、ソートされた配列から平均値が選択されます。 この値は、現在のピクセルの出力です。
以下は、コアサイズが3のメディアンフィルターです。
浸食と建物のフィルター
フィルターのビルドアップとエロージョンは、それぞれ形態学的な拡大または縮小を行うために使用されます。 簡単に言えば、画像の場合、これは近傍から最大または最小強度のピクセルを選択することを意味します。

蓄積の結果として、明るいオブジェクトが増加し、侵食-暗いオブジェクトが増加します。
このフィルターは、入力画像とバイナリマトリックスを使用します。 バイナリマトリックスは、近傍の形状を決定します。 通常、近隣は円形です。
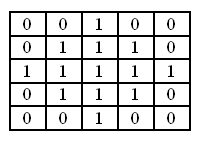
ビルドアップフィルターを使用して、グレア、明るい反射を増やすことができます。
おわりに
この記事では、画像処理フィルターのいくつかを説明し、アルゴリズムとアプリケーション機能について説明しました。
en.wikipedia.org/wiki/Median_filter
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
en.wikipedia.org/wiki/Math_Morphology
habrahabr.ru/post/43895