さらに、結果のシーケンスの品質は、擬似乱数ジェネレータ自体の実装の品質に依存します。 sayingにもあるように、「乱数生成は重要であり、偶然に任せることはできません」

擬似乱数ジェネレータを実装するための多くのオプションがあります。Yarrow、AES-256、SHA-1、MD5などの従来の暗号プリミティブを使用します。 Microsoft CryptoAPI エキゾチックなカオスとPRANDなど。
ただし、このメモの目的は異なります。 ここで、非常に人気のある1つの擬似乱数ジェネレーターの実用的な実装の機能を検討します。これは、たとえば/ dev /ランダム擬似デバイスのUnix環境や、電子機器やストリーム暗号を作成するときに広く使用されています。 LFSR(Linear Feedback Shift Register)についてです。
事実、密な多項式を使用する場合、LFSRレジスタの状態は非常にゆっくりと計算されると考えられています。 しかし、私が見るように、多くの場合、問題はアルゴリズム自体にあるのではなく(確かに理想的ではありませんが)、その実装にあります。
LFSRについて少し
文字通り、LFSRは線形フィードバックシフトレジスタであり、シフトレジスタとフィードバック関数という2つの部分で構成されています。 レジスタはビットで構成され、その長さはこれらのビットの数です。
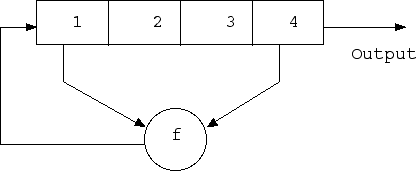
ビットが取得されると、レジスタのすべてのビットが1ポジションだけ右にシフトされます。 この場合、新しい左端のビットは、抽出前の残りのビットの機能によって決定されます。 最下位ビットは、レジスタの出力に表示されます。
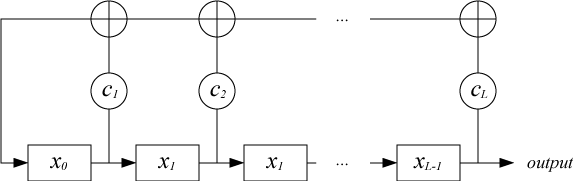
決定することは難しくないため、生成されたシーケンスのプロパティは、関連する多項式のプロパティと密接に関連しています。
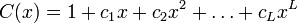
さらに、その非ゼロ係数はタップと呼ばれ、それに基づいてフィードバック関数の入力値が決定されます。
LFSRレジスタのビットフィールド長に応じた推奨タップインデックスは、ドキュメント「 Effective Shift Registers、LFSR Counters、およびLong PseudoRandom Sequence Generators 」に詳しく記載されています。
実用的な実装
そのため、LFSRの実装は非常に単純ですが、XORなどの密な多項式を計算するために多くのビット演算を使用するため、多くの場合、速度には多くのことが望まれます。 彼は「ウォームアップ」するのに時間が必要です。 代替案として、ガロアスキームを使用したLFSRの修正も提案されました。これは、約2倍の速度で実行されるLFSR関数の一定回数の呼び出しのサイクルです。
正直なところ、私はそれに同意できません。 私が見るように、多くの場合、問題はアルゴリズム自体ではなく、その実装にあります。 通常、次のタイプの構造が表示されます。
int LFSR (void) { static unsigned long S = 0xFFFFFFFF; /* taps: 32 31 30 28 26 1; charact. polynomial: x^32 + x^31 + x^30 + x^28 + x^26 + x^1 + 1 */ S = ((( (S>>0)^(S>>1)^(S>>2)^(S>>4)^(S>>6)^(S>>31) ) & 1 ) << 31 ) | (S>>1); return S & 1; }
残酷 ここでは、少なくとも、フラグレジスタのパリティフラグPF(パリティフラグ)の値を使用して、いくつかのXORとシフトを取り除くことができます。 実際、モジュロ2(XOR)の加算により、設定されたビット数のパリティが決まります。 結果の最下位バイトに偶数(0以外)のビットが含まれている場合、パリティフラグPFのみが設定されます。 少なくとも1つの算術シフトを行う必要があります。
xor ecx,ecx mov ebx,0FFFFFFFFh ; S mov eax,080000057h ; taps (32,31,30,28,26,1) and ebx,eax mov cl,ah sar ebx,018h lahf xor cl,ah sar cl,02h and cl,01h
密な多項式を使用する場合、タップが32ビットレジスタのビットフィールド全体に分散されると、4つのシフト演算と3つのXOR演算を既に受け取ります。
xor ecx,ecx mov ebx,0FFFFFFFFh ; S mov eax,095324C57h ; taps (32,31,30,28,26,22,21,18,15,12,11,8,6,4,1) and ebx,eax lahf mov cl,ah ; [0-7] bits sar ebx,08h lahf xor cl,ah ; [8-15] bits sar ebx,08h lahf xor cl,ah ; [16-23] bits sar ebx,08h lahf xor cl,ah ; [24-31] bits sar cl,02h and cl,01h
偏差:sar ebx、08hシフトの数が偶数またはゼロの場合、XORを実行する前にレジスタAHの値を反転する必要があります。これは、非ゼロビットの数が偶数のときにPFが設定されるためです。 そして、我々は反対が必要です。
どちらかといえばまだまだコーシャです:
int LFSR (void) { static unsigned long S = 0xFFFFFFFF; S = ((( (S>>0)^(S>>1)^(S>>2)^(S>>4)^(S>>6)^(S>>10)^(S>>11)^ (S>>14)^(S>>17)^(S>>20)^(S>>21)^(S>>24)^(S>>26)^ (S>>28)^(S>>31) ) & 1 ) << 31 ) | (S>>1); return S & 1; }
次の手順は、各LFSR状態でメモリに直接フラッシュする代わりに、レジスタを使用して結果を蓄積することです。
sal edx,01h or dl,cl
など、最大32の状態(edx DWORD)、その後のみメモリに書き込みます。
最後に、本当に高速な128ビットLFSRを(突然)実装する必要がある場合、MMXレジスタを使用できます。これにより、メモリアクセスを必要とせずに、レジスタのみでPentiumファミリの32ビットプロセッサにシフトを実装できます。
ソースコード
アセンブリ言語(x86)のソースコード: pastebin.com/rwKfsYsN
コンパイルされた実行可能コード: www.sendspace.com/file/atg0cf
更新:
最適化されたコードバージョン: pastebin.com/B3kPEaew
コンパイルされた実行可能コード: www.sendspace.com/file/9bl5di
- 128ビットLFSR
- 使用されたMMXレジスタ
- x86アーキテクチャ
- 変更2097120(0FFFFh x 32)LFSRレジスタのステータス
最後に
最後に、作業速度について-MMXとコーヒーレジスタフラグ(コーヒーディスプレイ)を使用して2 097 120(0FFFFh x 32)の状態を変更して128ビットLFSRを「ウォームアップ」すると、PCで約5秒かかりました。 同時に、上記と同様に書かれたC ++プログラムの実行は、128ビットバージョンと画面への出力に対して約2〜3分かかりました。
同時に、主な要点は、パリティフラグのユースケースでは、多項式密度はLFSRレジスタの新しい状態の逆関数の計算速度に大きな影響を与えないことです。 そして、それに応じて、次のスタイルのステートメント: 「RSLOSの主な問題の1つは、ソフトウェアの実装が非常に非効率的であるということです。 スパースフィードバック多項式は、相関の破れによって簡単にクラッキングされるため、避ける必要があります。 そして、密な多項式は非常にゆっくりと計算されます'' (ここから: ru.wikipedia.org/wiki/LFSR )はいくぶん...容認できず説明が必要です:)
psそして興味深いのは、アセンブラーを挿入せずに、128ビットLFSRの2 097 120(0FFFFh x 32)の状態を列挙するときの実行時間は、たとえば0.5秒未満で、高レベル言語でプログラムを実装できることです。