...またはコンソールアプリケーション用にAlenkaを取得した方法
さまざまなテストタスクを実装することで、プロのレベルを迅速に高めることができるという意見がかなり広まっています。 私自身は、時々トリッキーなテストスレッドを掘り下げて、常に良い状態になるように解決するのが好きです。 どういうわけか、ある会社でインターンシップの競争的な課題を完了していましたが、タスクは面白くて面白かったようです。その短いテキストを次に示します。
あなたの同僚の初心者が彼の困難な仕事について話しに来たと想像してください-彼は整数のセットを昇順に並べるだけでなく、LthからRthまでの順序セットのすべての要素を与える必要があります!
これは基本的なタスクであり、C#でソリューションを作成するのに10分かかると述べました。 まあ、または1時間。 または2。 またはチョコレート「Alyonka」
セットでは重複が許可され、要素の数は10 ^ 6以下であると想定されます。
ソリューションの評価にはいくつかのコメントがあります。
3人のプログラマーがコードを評価およびテストします。解決策は非常に興味深い可能性があるため、説明する必要があると考えました。
- Billは、10 KB以下のテストでソリューションを実行します。
- Stephenのテストでは、リクエストの数は10 ^ 5以下であり、追加のリクエストの数は100以下です。
- マークのテストでは、クエリの数は10 ^ 5以下です。
解決策
抽象リポジトリを用意しましょう。
追加(e)-アイテムをストアに追加し、範囲(l、r)-lからr要素へのスライスを示します。
簡単なストレージオプションは次のとおりです。
- ストレージは、昇順の動的配列に基づきます。
- バイナリ検索を挿入するたびに、要素を挿入する位置があります。
- Range(l、r)を照会するとき、単純に配列のスライスをlからrに取ります。
C範囲(l、r)-スライスを取ることはO(r-l)と推定できます。
C追加(e)-最悪の場合の挿入はO(n)に対して機能します。ここで、nは要素の数です。 n〜10 ^ 6の場合、挿入がボトルネックになります。 改善されたストレージオプションは、この記事の後半で提案されます。
ソースコードの例はここにあります 。
より適切なオプションは、たとえば次のとおりです。
- リポジトリの基礎は、挿入、検索、削除操作(AVLツリー、RBツリーなど)にO(ln n)の複雑さを持つ自己バランス検索ツリーです。
- サブツリー内のノードの数に関する情報をノードに追加することにより、データ構造が拡張されます。 これは、O(ln n)のツリーのi番目の要素を取得するために必要です。
- サブツリー内のノードの数を再カウントするために、アイテムがツリーに追加されます。 これは、追加操作のコストがO(ln n)のままになるようにすることができます。
スキップリスト
Skiplistは、複数のリンクリストに基づいて、検索ツリーのランダムな代替手段です。 1989年にWilliam Pughによって発明されました。 検索、挿入、および削除の操作は、対数的にランダムな時間で実行されます。
このデータ構造は広く知られていません(ちなみに、 Habréには非常に豊富に記述されています )が、漸近的な推定値は良好です。 好奇心のために、私はそれを実現したかった、さらに適切なタスクがあった。
さらに、私が解決に使用したすべてのソースからの簡単な絞り込みを行います。
ソートされた、単純に接続されたリストがあるとします:

最悪の場合、検索はO(n)で実行されます。 どのように加速できますか?
私が仕事をしているときにレビューしたビデオ講義の1つで、ニューヨークの急行列車について素晴らしい例を挙げました。

- スピードラインはいくつかのステーションを接続します
- 通常の線がすべてのステーションを接続します
- 一般的なスピードラインステーションの間に定期的なラインがあります
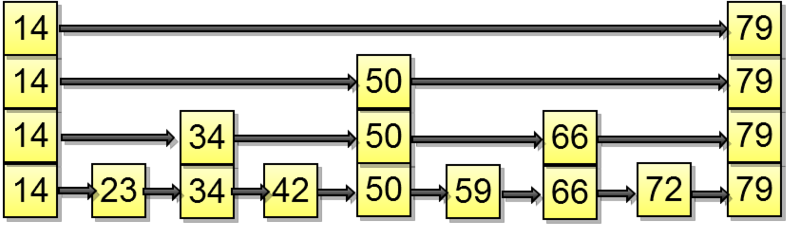
完全なSkipListが例に示されており、実際にはすべてが似ていますが、少し間違っています:)
検索する
これが検索方法です。 72番目の要素を探しているとします。
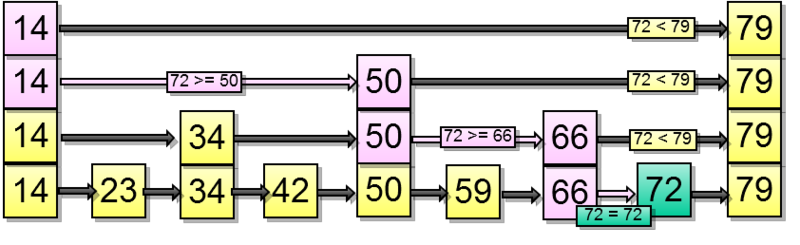
挿入
挿入では、物事はもう少し複雑です。 要素を挿入するには、一番下のリストのどこに挿入するかを理解し、同時に特定の数の上位レベルにそれをプッシュする必要があります。 しかし、それぞれの特定の要素をプッシュするためにいくつのレベルが必要ですか?
この方法で解決することが提案されています。挿入するとき、新しい要素を最低レベルに追加し、ドロップするまでコインを投げ始め、その要素を次の上位レベルにプッシュします。
要素を挿入してみましょう-67。まず、以下のリストのどこに要素を挿入するかを見つけます。
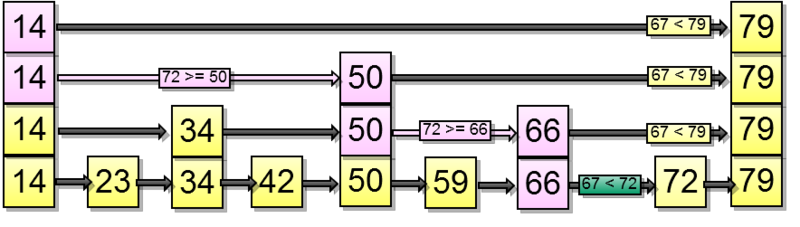
彼はコインが連続して2回落ちることを提案した。 したがって、要素を2レベル上にプッシュする必要があります。
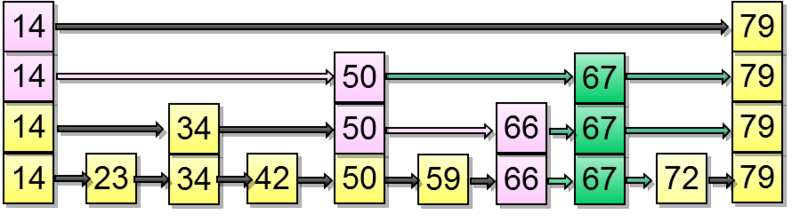
インデックスアクセス
インデックスでアクセスするには、次の操作を行うことをお勧めします。各遷移をその下にあるノードの数でマークします。
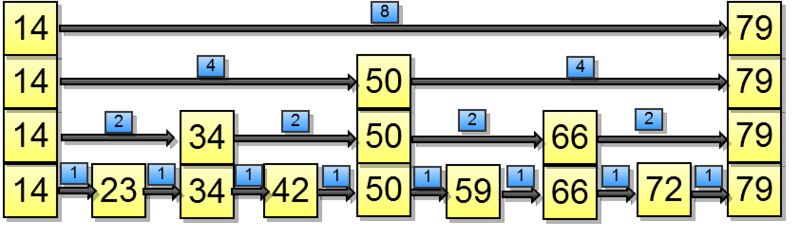
i番目の要素にアクセスした後(ところで、O(ln n)で取得します)、カットするのは難しくないようです。
Range(5、7)を見つける必要があるとします。 まず、インデックス5の要素を取得します。
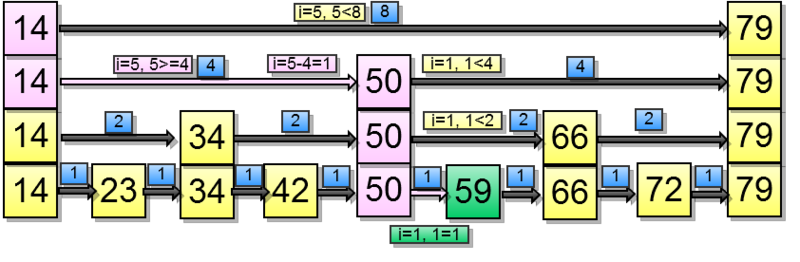
そして今、範囲(5、7):
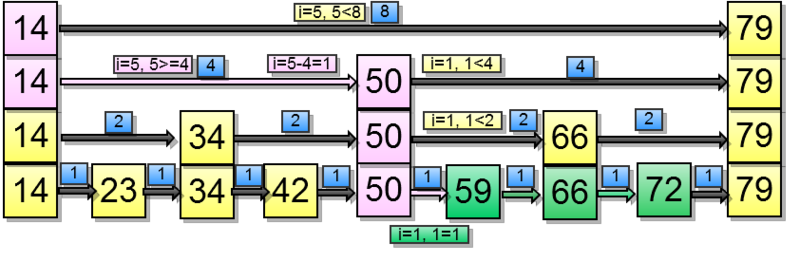
実装について
SkipListノードが次のような場合、実装は自然なようです。
実際、これはWilliam PugによるCの実装で行われました 。SkipListNode {
int Element;
SkipListNode[] Next;
int [] Width;
}
しかし、C#では、その長さも配列に格納されますが、可能な限り最小のメモリ量で実行したかった(判明したように、タスクの条件では、すべてが厳密に評価されていませんでした)。 同時に、SkipListの実装と拡張RBツリーがほぼ同じ量のメモリを使用するようにしました。
メモリ消費量を削減するための答えは、java.util.concurrentパッケージのConcurrentSkipListMapを詳しく調べると、予想外に見つかりました。
二次元スキップリスト
1つのディメンション内のすべての要素の単純に接続されたリストがあるとします。 2番目の方法では、下位レベルへのリンクを持つ遷移の「エクスプレスライン」があります。
ListNode {
int Element;
ListNode Next;
}
Lane {
Lane Right;
Lane Down;
ListNode Node;
}
不誠実なコイン
メモリ消費を削減するには、「不正な」コインを使用します。要素を次のレベルにプッシュする可能性を減らします。 William Pughは、いくつかのプッシュ確率値のスライスをレビューしました。 ½との値を検討する場合、実際には、メモリ消費量を削減してほぼ同じ検索時間が得られました。
乱数生成について少し
ConcurrentSkipListMapの基本を詳しく調べると、次のように乱数が生成されていることに気付きました。
この記事では、 XOR を使用して擬似乱数を生成する方法について詳しく読んでください 。 速度の特定の向上に気付かなかったため、使用しませんでした。int randomLevel() {
int x = randomSeed;
x ^= x << 13;
x ^= x >>> 17;
randomSeed = x ^= x << 5;
if ((x & 0x80000001) != 0)
return 0;
int level = 1;
while (((x >>>= 1) & 1) != 0) ++level;
return level;
}
結果のストレージのソースコードは、 ここで表示できます 。
一緒にgooglecode.com (プロジェクトページネーション )からピックアップできます。
テスト
3種類のストレージが使用されました。
- ArrayBased(動的配列)
- SkipListBased(パラメーター¼のスキップリスト)
- RBTreeBased(赤黒木:同様のタスクを実行した友人の実装)。
- 昇順アイテム
- 降順アイテム
- ランダムアイテム
結果:
| 配列 | RBTree | スキップリスト | |
|---|---|---|---|
| ランダム | 127033ミリ秒 | 1020ミリ秒 | 1737ミリ秒 |
| 注文済み | 108ミリ秒 | 457ミリ秒 | 536ミリ秒 |
| 降順 | 256337ミリ秒 | 358ミリ秒 | 407ミリ秒 |
測定も行われました:各ストレージに10 ^ 6個の要素が挿入された状態でメモリにどれくらいかかるか。 スタジオプロファイラーが使用されました。簡単にするために、次のコードが起動されました。
結果:var storage = ...
for ( var i = 0; i < 1000000; ++i)
storage.Add(i);
| 配列 | RBTree | スキップリスト | |
|---|---|---|---|
| 割り当てられた合計バイト | 8,389,066バイト | 24,000,060バイト | 23,985,598バイト |
アリヨンカとのハッピーエンド
問題の状況に応じて、同僚、泣き言を言う人が、私のためにバーを開いた。 私の決定は最高得点とされました。 誰かがこの記事が役立つことを願っています。 ご質問があれば、喜んでお答えします。
PS:SKB Konturでインターンシップに参加しました。 これは同じ質問に答えることではありません=)