ゲーム開発者向けの線形代数

この記事は、ゲーム開発者向けの4つの記事シリーズ、線形代数の翻訳であり、David Rosenによって線形代数とゲーム開発におけるその応用について書かれています。 元の記事は、 パート 1 、 パート2 、 パート3 、およびパート4にあります。 翻訳を別のトピックで公開するのではなく、すべての記事を1つにまとめました。 素材を知覚し、それを使って作業する方が便利だと思います。 それでは始めましょう。

なぜ線形代数が必要なのですか？

線形代数の方向の1つは、ベクトルの研究です。 ゲームで画面上のボタンの配置を使用し、カメラとその方向、オブジェクトの速度を操作する場合、ベクトルを処理する必要があります。 線形代数をよく理解すればするほど、ベクトルの振る舞い、ひいてはゲームをより細かく制御できます。

ベクターとは何ですか？

ゲームでは、ベクトルは位置、方向、速度を保存するために使用されます。 以下は、2次元ベクトルの例です。



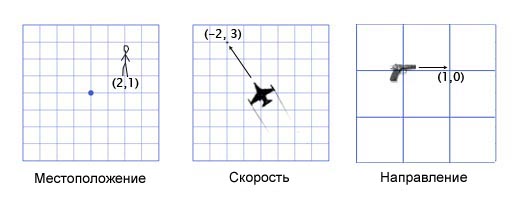
ロケーションベクトル（ "半径ベクトル"とも呼ばれます）は、人が出発点から東2メートル、北1メートルにあることを示します。 速度ベクトルは、時間単位で平面が3キロメートル上、左に2キロメートル移動することを示しています。 方向ベクトルは、銃が右を向いていることを示しています。



ご覧のとおり、ベクトル自体は、コンテキストに応じて何らかの意味を持つ数字のセットにすぎません。 たとえば、ベクトル（1、0）は、図に示すように武器の方向と、現在の位置から1マイル東にある構造体の座標の両方になります。 または、1時間あたり1マイルの速度で右に移動するカタツムリの速度（ 翻訳者のメモ：カタツムリの場合はかなり速い、1秒あたり44センチメートル ）。



ユニットを追跡することが重要です。 ベクトルV（3,5,2）があるとします。 これはほとんどわかりません。 3つの理由、5つの理由は？ オーバーグロースゲームでは、距離はメートルで、速度はメートル/秒で示されます。 このベクトルの最初の数値は東方向、2番目は上方向、3番目は北方向です。 負の数値は、西、下、南の反対方向を示します。 次の図に示すように、ベクトルV（3,5,2）で定義された位置は、東3メートル、上5メートル、北2メートルにあります。







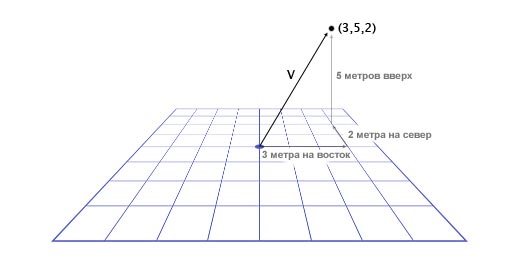
それで、ベクトルを扱う基本を学びました。 次に、ベクターの使用方法を学びます。

ベクトル加算

ベクトルを追加するには、それぞれのコンポーネントを互いに追加するだけです。 例：



（0、1、4）+（3、-2、5）=（0 + 3、1-2、4 + 5）=（3、-1、9）



なぜベクターを追加する必要があるのですか？ ほとんどの場合、ゲームでのベクトルの追加は物理的な統合に使用されます。 物理オブジェクトには、位置、速度、加速度のベクトルが含まれます。 各フレーム（通常は60分の1秒）で、2つのベクトルを統合する必要があります。位置に速度を追加し、速度に加速度を追加します。



マリオジャンプの例を見てみましょう。 位置（0、0）から始まります。 ジャンプが開始された瞬間、その速度（1、3）で、すぐに右上に移動します。 重力によって引き下げられるため、加速度は（0、-1）です。 写真は、彼のジャンプがどのように見えるかを7つのフレームに分けて示しています。 黒いテキストは、各フレームの速度を示しています。







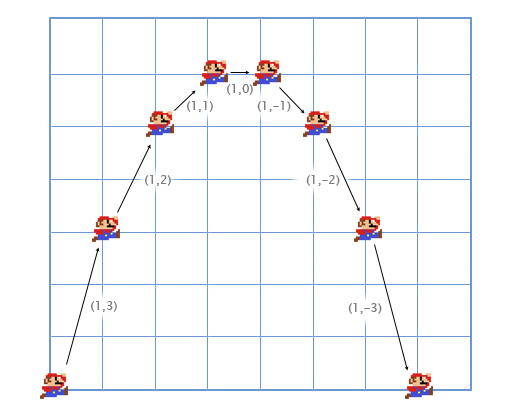
最初のフレームを詳細に見て、すべてがどのように起こるかを理解しましょう。



最初のフレームでは、マリオの速度（1、3）をその位置（0、0）に追加し、新しい座標（1、3）を取得します。 次に、加速度（0、-1）に速度（1、3）を追加し、マリオの速度（1、2）の新しい値を取得します。



2番目のフレームにも同じことを行います。 位置（1、3）に速度（1、2）を追加し、座標（2、5）を取得します。 次に、速度（1、2）に加速度（0、-1）を追加し、新しい速度（1、1）を取得します。



通常、プレーヤーはキーボードまたはゲームパッドを使用してゲームキャラクターの加速を制御し、ゲームは物理的な追加（ベクトルの追加による）を使用して速度と位置の新しい値を計算します。 これは積分計算で解決されるのと同じ問題であり、ゲームのために単純化するだけです。 先ほど説明した実際の応用について考えて、積分計算に関する講義を注意深く聞く方がはるかに簡単であることに気付きました。

ベクトルの減算

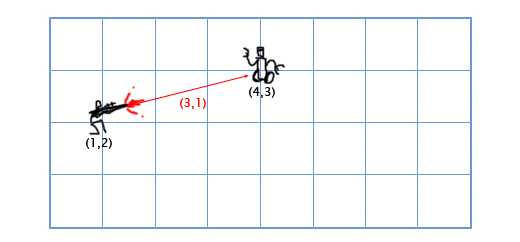
減算は加算と同じ原理に従って計算されます-ベクトルの対応する成分を減算します。 ベクトルの減算は、ある場所から別の場所までを示すベクトルを取得するのに便利です。 たとえば、プレーヤーがレーザー銃の座標（1、2）にあり、敵ロボットが座標（4、3）にあるとします。 ロボットに当たるレーザービームの動きベクトルを決定するには、ロボットの位置からプレイヤーの位置を減算する必要があります。 取得するもの：



（4、3）-（1、2）=（4-1、3-2）=（3、1）。

ベクトルにスカラーを掛ける

ベクトルについて話すとき、個々の数値をスカラーと呼びます。 たとえば、（3、4）はベクトルで、5はスカラーです。 ゲームでは、多くの場合、ベクトルに数値（スカラー）を掛ける必要があります。 たとえば、各フレームでプレーヤーの速度に0.9を掛けて、単純な空気抵抗をシミュレートします。 これを行うには、ベクトルの各コンポーネントをスカラーで乗算する必要があります。 プレーヤーの速度が（10、20）の場合、新しい速度は次のようになります。



0.9 *（10、20）=（0.9 * 10、0.9 * 20）=（9、18）。

ベクトルの長さ

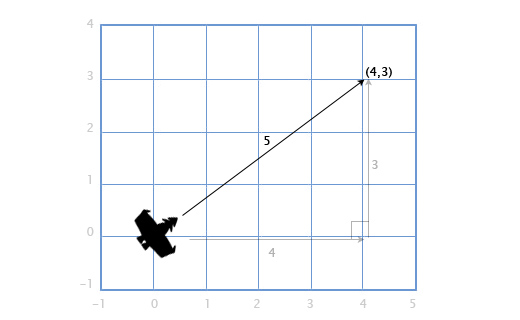
速度ベクトルV（4、3）の船がある場合、スクリーンスペースの必要性または必要な燃料量を計算するためにどれだけ速く動くかを調べる必要もあります。 これを行うには、ベクトルVの長さ（モジュール）を見つける必要があります。ベクトルの長さは垂直線で示されます。この場合、ベクトルVの長さは| V |と示されます。



Vを辺4と3の直角三角形として表すことができ、ピタゴラスの定理を使用して、式から斜辺を取得します。x ² + y ² = h ²



この場合、平方根から成分（x、y）を持つベクトルHの長さを取得します：sqrt（x ² + y ² ）。



したがって、私たちの船の速度は次のとおりです。



| V | = sqrt（4 ² + 3 ² ）= sqrt（25）= 5







このアプローチは、3次元ベクトルにも使用されます。 成分（x、y、z）を含むベクトルの長さは、sqrt（x ² + y ² + z ² ）として計算されます。

距離

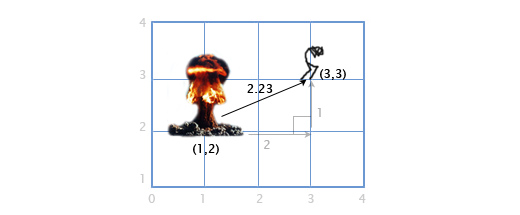
プレイヤーPがポイント（3、3）にあり、爆発がポイントEで座標（1、2）によって発生した場合、プレイヤーに与えられたダメージの程度を計算するために、プレイヤーと爆発の間の距離を決定する必要があります。 これは、上記の2つの操作（ベクトルとその長さの減算）を組み合わせることで簡単に実行できます。

P-Eを減算して、それらの間のベクトルを取得します。 次に、このベクトルの長さを決定します。これにより、望ましい距離が得られます。 オペランドの順序はここでは関係ありません| E-P | 同じ結果が得られます。



距離= | P-E | = |（3、3）-（1、2）| = |（2、1）| = sqrt（2 ² +1 ² ）= sqrt（5）= 2.23

正規化

（位置や速度ではなく）方向を扱う場合、方向ベクトルの長さが1に等しいことが重要です。 これは私たちの生活を大幅に簡素化します。 たとえば、銃が（1、0）方向に展開され、毎秒20メートルの速度で発射体を発射するとします。 この場合、発射された発射体の速度ベクトルは何ですか？



方向ベクトルの長さは1に等しいので、方向に発射体の速度を掛けて、速度ベクトル（20、0）を取得します。 ただし、方向ベクトルの長さが1以外の場合、これを行うことはできません。 発射物は速すぎるか遅すぎるかのいずれかです。



長さが1に等しいベクトルは、「正規化」と呼ばれます。 ベクトルを正規化する方法は？ とても簡単です。 ベクトルの各コンポーネントをその長さで除算します。 たとえば、ベクトルVをコンポーネント（3、4）で正規化する場合、各コンポーネントをその長さで、つまり5で除算し、（3/5、4/5）を取得します。 次に、ピタゴラスの定理を使用して、その長さが1に等しいことを確認します。



（3/5） ² +（4/5） ² = 9/25 + 16/25 = 25/25 = 1

ベクトルのスカラー積

スカラー積（•と表記）とは何ですか？ 2つのベクトルのスカラー積を計算するには、それらの成分を乗算し、結果を加算する必要があります



（a1、a2）•（b1、b2）= a1b1 + a2b2



例：（3、2）•（1、4）= 3 * 1 + 2 * 4 =11。これは一見無駄に思えますが、詳しく見てみましょう。







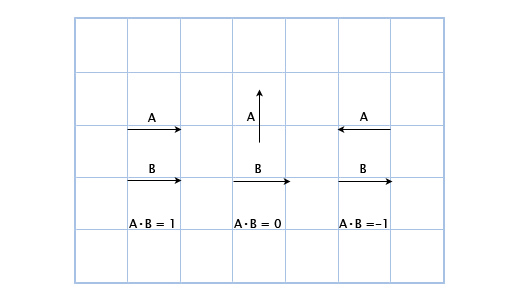
ここで、ベクトルが一方向を指している場合、それらのスカラー積はゼロより大きいことがわかります。 それらが互いに垂直である場合、スカラー積はゼロです。 そして、それらが反対方向を指すとき、それらのスカラー積はゼロ未満です。

基本的に、ベクトルのスカラー積を使用して、一方向にどれだけのベクトルがあるかを計算できます。 そして、これはスカラー積の可能性のほんの一部にすぎませんが、すでに非常に便利です。



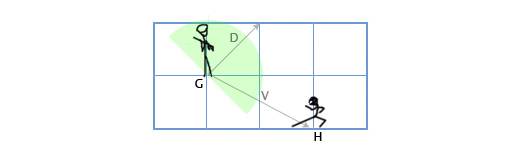
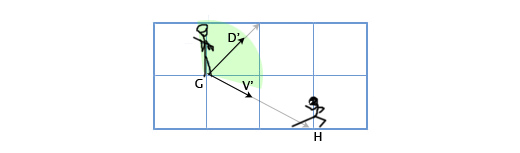
G（1、3）に位置し、180度の視角で方向D（1,1）を見ているガードがあるとします。 ゲームの主人公はH（3、2）の位置から彼をスパイします。 主人公が警備員の視界にいるかどうかを判断する方法は？ これは、ベクトルDとV（ガードからメインキャラクターに向けられたベクトル）のスカラー積によって行います。 次のものが得られます。



V = H-G =（3、2）-（1、3）=（3-1、2-3）=（2、-1）

D•V =（1、1）•（2、-1）= 1 * 2 + 1 * -1 = 2-1 = 1



単位はゼロより大きいため、主人公は警備員の視界にいます。







スカラー積がベクトルの方向の決定に関連していることはすでにわかっています。 そして、より正確な定義は何ですか？ ベクトルのスカラー積の数学表現は次のようになります。



A•B = | A || B |cosΘ



ここで、Θ（「シータ」と発音）は、ベクトルAとBの間の角度です。



これにより、次の式を使用してΘ（角度）を見つけることができます。



Θ= acos（[AB] / [| A || B |]）



前述したように、ベクトルの正規化は私たちの生活を簡素化します。 AとBが正規化されている場合、式は次のように簡略化されます。



Θ= acos（AB）



ガードシナリオをもう一度見てみましょう。 ガードの角度が120度に等しくなるようにします。 ガードの保護（D '）およびガードからメインキャラクターへの誘導（V'）の正規化されたベクトルを取得します。 次に、それらの間の角度を決定します。 角度が60度（視野角の半分）を超える場合、主人公はガードから見えなくなります。



D '= D / | D | =（1、1）/ sqrt（1 ² + 1 ² ）=（1、1）/ sqrt（2）=（0.71、0.71）

V '= V / | V | =（2、-1）/ sqrt（2 ² +（-1） ² ）=（2、-1）/ sqrt（5）=（0.89、-0.45）



Θ= acos（D'V '）= acos（0.71 * 0.89 + 0.71 *（-0.45））= acos（0.31）= 72



警備員の視界の中心と主人公の位置との間の角度は72度であるため、警備員は彼を見ません。







これはかなり複雑に見えますが、これはすべてを手動で行うためです。 プログラムでは、すべて非常に簡単です。 以下は、私が書いたC ++ベクトルライブラリを使用して、 Overgrowthゲームでこれをどのように行ったかを示しています。

//  vec2 guard_pos = vec2(1,3); vec2 guard_facing = vec2(1,1); vec2 hero_pos = vec2(3,2); //   vec2 guard_facing_n = normalize(guard_facing); vec2 guard_to_hero = normalize(hero_pos - guard_pos); //  float angle = acos(dot(guard_facing_n, guard_to_hero));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ベクターアートワーク

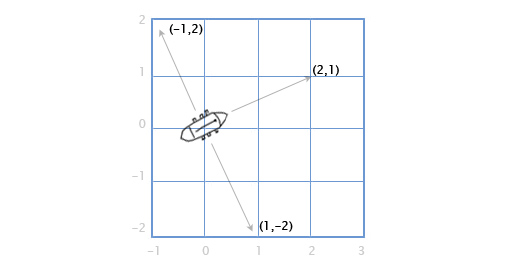
コースの右側と左側を撃つ大砲を備えた船があるとします。 ボートが方向ベクトル（2、1）に沿って配置されていると仮定します。 銃はどの方向に射撃しますか？



2次元グラフィックスでは非常に簡単です。 方向を時計回りに90度回転するには、ベクトルのコンポーネントを交換し、2番目のコンポーネントの符号を変更します。

（a、b）は（b、-a）になります。 したがって、ベクトル（2、1）に沿って位置する船では、右board側の銃は方向（1、-2）で発砲し、左port側の銃は反対方向に発砲します。 ベクトルの成分の符号を変更し、（-1、2）を取得します。







しかし、3次元グラフィックスのすべてを計算したい場合はどうでしょうか？ 船の例を考えてみましょう。

マストベクトルMは真上（0、1、0）に向けられ、風向は北北東E W（1、0、2）です。 そして、最良の方法で「風をキャッチ」するために、帆Sの方向ベクトルを計算します。



この問題を解決するには、ベクトル積S = M x Wを使用します。







A（a ₁ 、a ₂ 、a ₃ ）とB（b ₁ 、b ₂ 、b ₃ ）のベクトル積は次のようになります。



（a ₂ b ₃ -a ₃ b ₂ 、a ₃ b ₁ -a ₁ b ₃ 、a ₁ b ₂ -a ₂ b ₁ ）



次に、必要な値を置き換えます。



S = MxW =（0、1、0）x（1、0、2）=（[1 * 2-0 * 0]、[0 * 1-0 * 2]、[0 * 0-1 * 1] ）=（2、0、-1）



手動計算では非常に困難ですが、グラフィカルアプリケーションやゲームアプリケーションでは、以下に示すような関数を記述し、そのような計算の詳細には触れないことをお勧めします。

 vec3 cross(vec3 a, vec3 b) { vec3 result; result[0] = a[1] * b[2] - a[2] * b[1]; result[1] = a[2] * b[0] - a[0] * b[2]; result[2] = a[0] * b[1] - a[1] * b[0]; return result; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

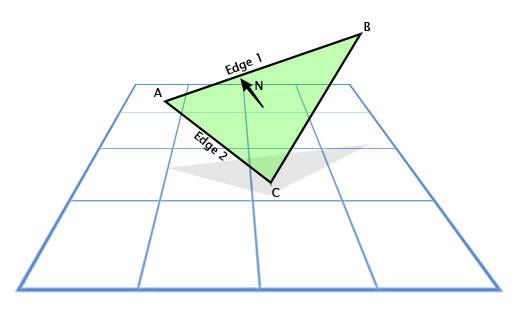
ベクトル積は、ゲームで表面法線を計算するためによく使用されます。 これまたはその表面が「見える」方向。 たとえば、頂点A、B、Cのベクトルを持つ三角形を考えてみましょう。三角形が「見える」方向、つまりその平面に垂直な方向をどのようにして見つけるのでしょうか。 複雑に思えますが、この問題を解決するツールがあります。



減算を使用して、AからCへの方向（C-A）を決定し、「face 1」（エッジ1）、AからBへの方向（B-A）、「face 2」（エッジ2）にします。 。 そして、ベクトル積を適用して、両方に垂直な、つまり「平面の法線」とも呼ばれる三角形の平面に垂直なベクトルを見つけます。







これはコードでどのように見えるかです：

 vec3 GetTriangleNormal(vec3 a, vec3 b, vec3 c) { vec3 edge1 = ba; vec3 edge2 = ca; vec3 normal = cross(edge1,edge2); return normal; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ゲームでは、照明の主な表現はN•Lとして記述されます。ここで、Nは照明された表面の法線、Lは光の正規化された方向ベクトルです。 その結果、光が直接当たると表面は明るく見え、光が当たらないと表面が暗くなります。



ここで、ゲーム開発者にとって「変換マトリックス」（変換マトリックス）のような重要な概念を検討します。



まず、変換マトリックスの「ビルディングブロック」を調べます。

基本ベクトル

非常に古いハードウェアで小惑星ゲームを書いており、その平面内で自由に回転できる単純な2次元の宇宙船が必要だとします。 船のモデルは次のようになります。







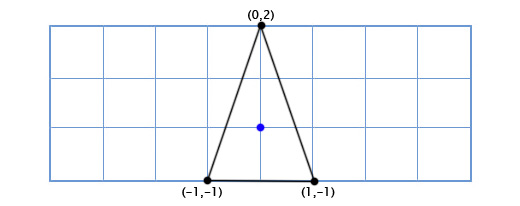
プレイヤーが任意の角度、たとえば反時計回りに49度回転したときに、どのように船を描画しますか。 三角法を使用して、ポイントの座標と回転角度を取得し、オフセットポイントの座標を返す2次元回転関数を作成できます。

 vec2 rotate(vec2 point, float angle){ vec2 rotated_point; rotated_point.x = point.x * cos(angle) - point.y * sin(angle); rotated_point.y = point.x * sin(angle) + point.y * cos(angle); return rotated_point; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この関数を3つのポイントすべてに適用すると、次の図が得られます。







サインとコサインの操作はかなり遅くなりますが、3ポイントのみの計算を行うため、これは古いハードウェアでも正常に機能します（ 翻訳者の注意：メモリテーブルは関数ごとに整理され、アプリケーションの起動時に計算されます。その後、三角関数を計算するときにテーブルにアクセスするだけです ）。



次に、船を次のようにします。







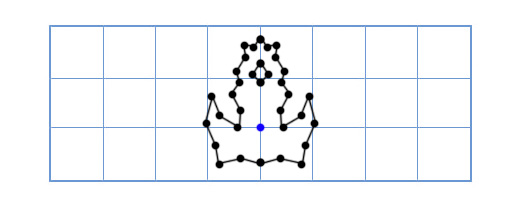
かなり多数のポイントを回転させる必要があるため、古いアプローチは非常に遅くなります。 この問題に対するエレガントな解決策の1つは、次のように聞こえます。「船のモデルの各ポイントを回転させる代わりに、モデルの座標グリッドを回転させるとどうなるでしょうか？」







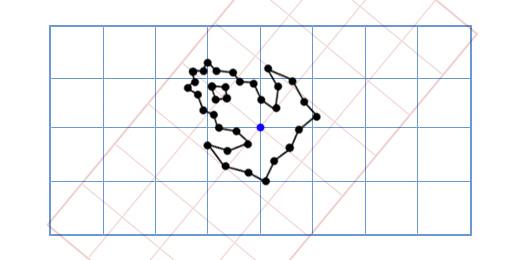
どのように機能しますか？ 座標が何であるかを詳しく見てみましょう。

座標（3、2）を持つポイントについて話すとき、その位置は、X座標軸に沿った基準点から3ステップ、Y座標軸に沿った基準点から2ステップであると言います。



デフォルトでは、座標軸は次のように配置されます：座標軸Xのベクトル（1、0）、座標軸Yのベクトル（0、1）。 そして、位置を取得します：3（1、0）+ 2（0、1）。 ただし、座標軸はその位置にある必要はありません。 座標軸を回転させると、同時に座標グリッド内のすべてのポイントが回転します。



回転軸XおよびYを取得するには、上記の三角関数を使用します。 49度回転する場合、新しい座標軸Xはベクトル（0、1）を49度回転することにより取得され、新しい座標軸Yはベクトル（0、1）を49度回転することにより取得されます。 したがって、新しい軸Xのベクトルは（0.66、0.75）に等しくなり、新しい軸Yのベクトルは（-0.75、0.66）になります。 単純な3点モデルを手動で実行して、正常に機能することを確認します。



上の点の座標は（0、2）です。つまり、新しい位置は新しい（回転した）X軸では0、新しいY軸では2になります。



0 *（0.66.0.75）+ 2 *（-0.75、0.66）=（-1.5、1.3）



左下のポイントは（-1、-1）です。つまり、その新しい位置は、回転したX軸で-1、回転したY軸で-1です。



-1 *（0.66.0.75）+ -1 *（-0.75、0.66）=（0.1、-1.4）



右下のポイントは（1、-1）です。これは、新しい位置が回転したX軸で1、回転したY軸で-1であることを意味します。



1 *（0.66.0.75）+ -1 *（-0.75、0.66）=（1.4、0.1）







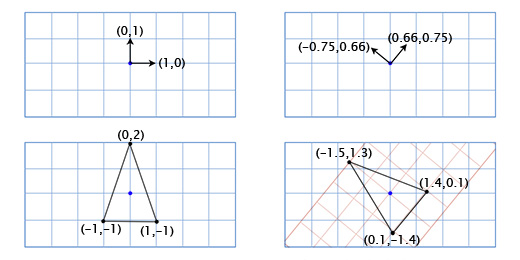
回転軸（または「ベースベクトル」）を持つ別の座標グリッドに船の座標がどのように表示されるかを示しました。 これは、船舶モデルの各ポイントに三角変換を適用する必要がないため、この場合に便利です。



基底ベクトル（1、0）と（0、1）を（a、b）と（c、d）に変更するたびに、次の式を使用して点（x、y）の新しい座標を見つけることができます。



x（a、b）+ y（c、d）



通常、基底ベクトルは（1、0）と（0、1）であり、x（1、0）+ y（0、1）=（x、y）が得られるだけなので、これをさらに処理する必要はありません。 ただし、必要なときに他の基底ベクトルを使用できることを覚えておくことが重要です。

行列

行列は2次元ベクトルに似ています。 たとえば、典型的な2x2マトリックスは次のようになります。

    [acbd]

行列にベクトルを掛ける場合、各行のスカラー積と乗算が発生するベクトルを合計します。 たとえば、上記の行列にベクトル（x、y）を掛けると、次のようになります。



（a、c）•（x、y）+（b、d）•（x、y）



書き方が異なると、この式は次のようになります。



x（a、b）+ y（c、d）



おなじみですね。 これは、基底ベクトルを変更するために使用した式とまったく同じです。 これは、2x2行列に2次元ベクトルを掛けることにより、基底ベクトルを変更することを意味します。 たとえば、マトリックスの列の（1、0）および（0、1）に標準基底ベクトルを挿入すると、次のようになります。

 [1 0 
  0 1]

これは、指定したニュートラル基底ベクトルから期待できる効果を生成しない単位行列です。 ただし、基底ベクトルを49度回転すると、次のようになります。

 [0.66 -0.75 
  0.75 0.66]

この行列は、2次元ベクトルを反時計回りに49度回転します。 このような行列を使用して、Asteriodsゲームのコードをよりエレガントにすることができます。 たとえば、船の回転関数は次のようになります。

 void RotateShip(float degrees){ Matrix2x2 R = GetRotationMatrix(degrees); for(int i=0; i<num_points; ++i){ rotated_point[i] = R * point[i]; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ただし、このマトリックスに宇宙船の動きも含めることができれば、コードはさらにエレガントになります。 次に、オブジェクトの方向と空間内の位置に関する情報を格納および適用する単一のデータ構造を作成します。



幸いなことに、これを実現する方法がありますが、非常にエレガントに見えません。 ベクトル（e、f）を使用して移動する場合は、変換行列にのみ含めます。

 [acebdf 0 0 1]

そして、次のように、オブジェクトの位置を決定する各ベクトルの最後に追加のユニットを追加します。



[xy 1]



今、それらを掛けると、次のようになります：



（a、c、e）•（x、y、1）+（b、d、f）•（x、y、1）+（0、0、1）•（x、y、1）



これは、次のように記述できます。



x（a、b）+ y（c、d）+（e、f）



これで、1つのマトリックスに囲まれた完全な変換メカニズムができました。 これは、コードの優雅さを考慮しない場合に重要です。コードを使用すると、標準のマトリックス操作をすべて使用できるようになるためです。 たとえば、マトリックスを乗算して目的の効果を追加したり、マトリックスを反転してオブジェクトの正確な反対の位置を取得したりできます。

3Dマトリックス

3次元空間の行列は、2次元の行列と同じように機能します。 2次元の画像を表示するディスプレイを使用すると簡単に表示できるため、2次元のベクトルと行列を使用した例を示しました。 基本ベクトルには、2つではなく3つの列を定義する必要があります。 基底ベクトルが（a、b、c）、（d、e、f）および（g、h、i）の場合、マトリックスは次のようになります。

 [adgbehcfi]

（j、k、l）を移動する必要がある場合、前に述べたように、追加の列と行を追加します。

 [adgjbehkcfil 0 0 0 1]
 

そして、次のように、ユニット[1]をベクトルに追加します。



[xyz 1]

二次元回転

私たちの場合、（ディスプレイ上にある）回転軸が1つしかないため、知る必要があるのは角度だけです。 これについては、三角関数を使用して、次のような2次元回転関数を実装できることを説明しました。

 vec2 rotate(vec2 point, float angle){ vec2 rotated_point; rotated_point.x = point.x * cos(angle) - point.y * sin(angle); rotated_point.y = point.x * sin(angle) + point.y * cos(angle); return rotated_point; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは、マトリックス形式でよりエレガントに表現できます。 マトリックスを決定するために、角度Θの軸（1、0）と（0、1）にこの関数を適用し、マトリックスの列に結果の軸を含めることができます。 それでは、座標軸X（1、0）から始めましょう。 関数を適用すると、次の結果が得られます。



（1 * cos（Θ）-0 * sin（Θ）、1 * sin（Θ）+ 0 * cos（Θ））=（cos（Θ）、sin（Θ））



次に、座標軸Y（0、1）を含めます。 取得するもの：



（0 * cos（Θ）-1 * sin（Θ）、0 * sin（Θ）+ 1 * cos（Θ））=（-sin（Θ）、cos（Θ））



取得した座標軸をマトリックスに含め、2次元の回転マトリックスを取得します。

 [cos（Θ）-sin（Θ） 
  sin（Θ）cos（Θ）]

このマトリックスを、Blenderグラフィックパッケージの猿であるSusannahに適用します。 回転角Θは時計回りに45度です。







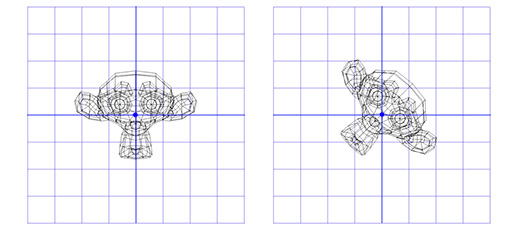
ご覧のとおり、動作します。 しかし、（0、0）以外の点を中心に回転する必要がある場合はどうでしょうか？

たとえば、サルの頭を耳にあるポイントの周りに回転させます。







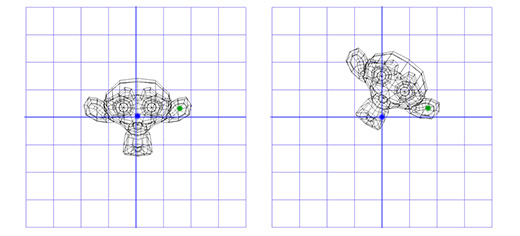
これを行うには、開始点から猿の耳の回転点にオブジェクトを移動する変換行列Tと、開始点を中心にオブジェクトを回転させる回転行列Rを作成することから始めます。 さて、耳にある点の周りを回転させるには、まずT ^-1と書かれた行列Tを反転することにより、耳の点を開始点の位置に移動します。 次に、マトリックスRを使用して開始点を中心にオブジェクトを回転させ、マトリックスTを適用して回転点を元の位置に戻します。

以下に、説明する各ステップの図を示します。







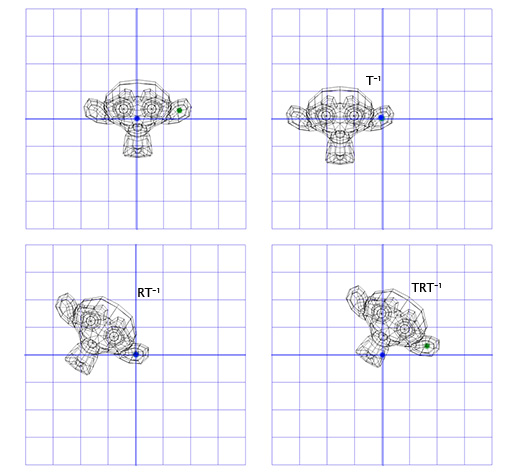
これは、後で適用する重要なテンプレートです。2つの反対の変換に回転を使用すると、オブジェクトを別の「空間」で回転させることができます。 これは非常に便利で便利です。



次に、3次元の回転を検討します。

3D回転

Z軸を中心とした回転は、2次元空間での回転と同じ原理で機能します。 列と行を追加して、古いマトリックスを変更するだけです。

 [cos（Θ）-sin（Θ）0 
  sin（Θ）cos（Θ）0 
  0 0 1]

このマトリックスを、Blenderパッケージの猿であるSusannaの3次元バージョンに適用します。 回転角Θは、時計回りに45度に等しくする必要があります。







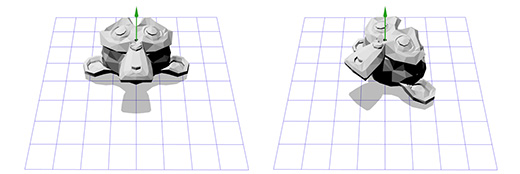
同じこと。 Z軸を中心に回転するだけでは制限されますが、任意の軸を中心に回転するのはどうですか？

軸角回転

軸と角度によって定義される回転の表現は、指数座標の回転とも呼ばれ、2つの量の回転によってパラメーター化されます。 ガイド軸（直線）の回転を定義するベクトルと、この軸の周りの回転量を表す角度。 回転は右手の規則に従って行われます。



そのため、回転は2つのパラメーター（軸、角度）で定義されます。ここで、軸は回転軸のベクトル、角度は回転角度です。 この手法は非常に単純であり、私が使用する他の多くの回転操作の出発点となります。 軸と角度によって決定される回転を実際に適用する方法は？



次の図に示すように、回転軸を扱っているとします。







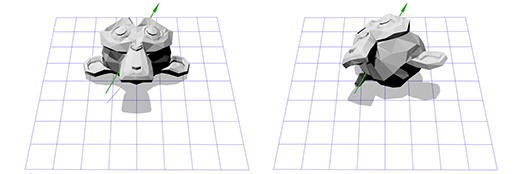
Z軸を中心にオブジェクトを回転させる方法を知っており、他の空間でオブジェクトを回転させる方法を知っています。 したがって、回転軸がZ軸になるスペースを作成するだけで、この軸がZ軸である場合、X軸とY軸はどうなりますか？ 計算をしましょう。



新しい軸XとYを作成するには、新しいZ軸に垂直で、互いに垂直な2つのベクトルを選択するだけです。 2つのベクトルを取り、それらに垂直なベクトルを与えるベクトル乗算については既に説明しました。



1つのベクトルがあります。これは回転軸です。Aと呼びましょう。次に、ベクトルAと同じ方向ではないランダムな他のベクトルBを取ります。たとえば、（0、0、1）とします。



回転軸AとランダムなベクトルBがあり、ベクトル積AとBを介して法線Cを取得できます。CはベクトルAとBに垂直です。次に、ベクトルBをベクトル積とベクトルAとCに垂直にします。 それだけです。必要なすべての座標軸があります。



言葉で言えば、これは複雑に聞こえますが、コードや写真に表示されると非常に単純に見えます。

以下は、これがコードでどのように見えるかを示しています。

 B = (0,0,1); C = cross(A,B); B = cross(C,A);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

各ステップの図を次に示します。







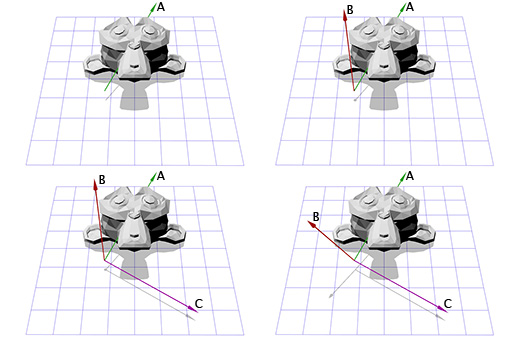
新しい座標軸に関する情報が得られたので、各軸をこの行列の列として含めることで行列Mを構成できます。 新しい座標軸Zになるように、ベクトルAが3番目の列であることを確認する必要があります。

 [B0 C0 A0 
  B1 C1 A1 
  B2 C2 A2]

これは、2次元空間で回転するために行ったことに似ています。 逆行列Mを使用して新しい座標系に移動し、行列Rに従って回転してオブジェクトをZ軸を中心に回転し、行列Mを適用して元の座標空間に戻すことができます。







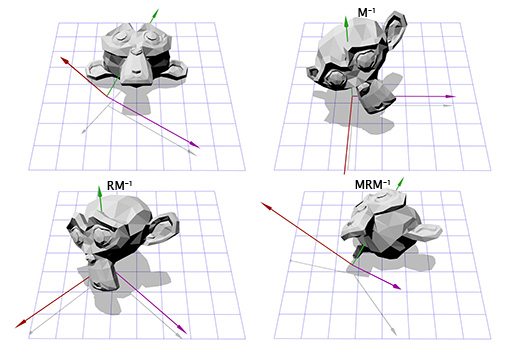
これで、任意の軸を中心にオブジェクトを回転できます。 最終的には、マトリックスT = T = M ^-1 RMを作成して、何度も使用することができます。 軸と角度で定義された回転を、マトリックスで定義された回転に変換するより効率的な方法があります。 先ほど説明したアプローチは、前に説明した多くのことを示しています。



軸と角度によって定義される回転は、おそらく最も直感的な方法です。 これを使用すると、角の記号を変更することで回転を反転するのが非常に簡単になり、角度を補間することで簡単に補間することができます。 ただし、重大な制限があり、そのような回転は合計ではないという事実にあります。 つまり、3番目の軸と角度で定義された2つの回転を組み合わせることはできません。

軸と角度で定義された回転は開始するのに良い方法ですが、より複雑な場合に使用するために他の何かに変換する必要があります。

オイラー角

オイラー角は、X、Y、Z軸を基準にネストされた3つの回転で構成される別の回転方法を表します。カメラが1人称または3人称のアクションを示すゲームで使用されることがあります。



一人称シューティングゲームをプレイし、左に30度回転してから40度見上げたとします。 最終的に、彼らはあなたを撃ち、あなたにぶつかり、一撃の結果として、カメラはその軸を中心に45度回転します。 オイラー角（30、40、45）を使用した回転を以下に示します。







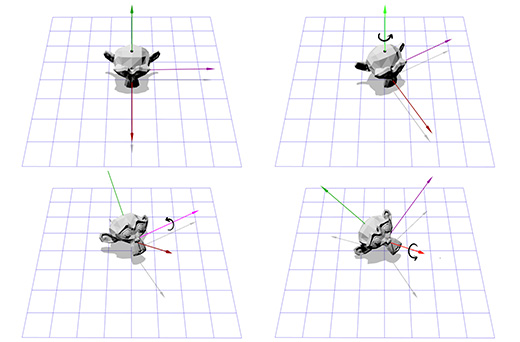
オイラー角は便利で使いやすいツールです。 しかし、この方法には2つの欠点があります。



1つは、 「軸ロック」または「ジンバルロック」と呼ばれる状況の可能性です。 一人称視点のシューティングゲームをプレイして、左、右、上下を見たり、カメラを視軸を中心に回転させたりすることを想像してください。 今、あなたがまっすぐ見上げていると想像してください。 この状況では、左または右を見ようとすることは、カメラを回転させようとすることに似ています。 この場合にできることは、カメラをその軸を中心に回転させるか、下を見ることです。 ご想像のとおり、この制限により、フライトシミュレータでオイラー角を使用することは実用的ではありません。



2番目-2つのオイラー回転角間の補間は、それらの間の最短経路を与えません。

たとえば、2つの同一の回転間に2つの補間があります。 1つ目はオイラー角補間を使用し、2つ目は球面線形補間（SLERP）を使用して最短経路を見つけます。







それでは、回転の補間により適しているのは何ですか？たぶんマトリックス？

マトリックス回転

前述したように、回転行列には3つの軸に関する情報が格納されます。これは、2つのマトリックス間の補間が各軸のみを線形補間することを意味します。その結果、これは私たちに効果的な方法を提供し、新しい問題ももたらします。たとえば、2つの回転と1つの補間された半回転を次に示します。







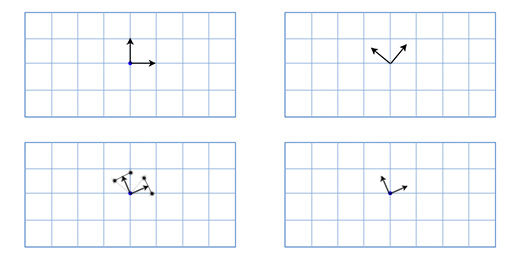
ご覧のとおり、補間された回転は元の回転よりもはるかに小さく、2つの軸は互いに垂直ではありません。考えてみると、これは論理的です-球体上の任意の2点を結ぶセグメントの中央は、球体の中心により近く配置されます。



これにより、骨格アニメーションを使用するときによく知られているキャンディラッパーエフェクトが発生します。以下は、オーバーグロースゲームのウサギの例を使用したこの効果のデモです。（ノート翻訳者：ウサギの体の真ん中に注意を払ってください）。







マトリックス操作に基づく回転は、ジンバルロックなどの問題なく回転を蓄積でき、シーン内のポイントに非常に効果的に適用できるため、非常に便利です。これが、マトリックス回転サポートがグラフィックカードに組み込まれている理由です。どのタイプの3次元グラフィックスでも、マトリックス回転形式は常に最終的に適用される方法です。



ただし、既に知っているように、マトリックスはあまりうまく補間されておらず、あまり直感的ではありません。



したがって、メインのローテーション形式は1つしかありません。最後に、それでも重要です。

四元数

クォータニオンとは何ですか？要するに、これは空間に存在する軸角度（軸角度回転）に基づいた代替回転です。



マトリックスと同様に、それらは回転を蓄積することができます。つまり、それらから回転のチェーンを作成することができ、恐れることなく、軸ロック（ジンバルロック）を取得できます。同時に、マトリックスとは異なり、ある位置から別の位置にうまく補間できます。



クォータニオンは他の回転形式よりも優れたソリューションですか？

今日では、他の回転方法のすべての長所を組み合わせています。しかし、それらには2つの弱点があり、どちらを検討したかによって、四元数が中間回転に最適であるという結論に達しました。四元数の欠点は何ですか。



第一に、四元数は3次元空間で表示するのは簡単ではありません。そして、我々は常により簡単な方法で回転を実装し、それを変換することを強制されます。第二に、四元数は効果的に点を回転させることができず、かなりの数の点を回転させるためにそれらを行列に変換することを余儀なくされます。



これは、クォータニオンを使用して一連の回転を開始または終了しない可能性が高いことを意味します。しかし、彼らの助けを借りて、他のアプローチよりも効率的に中間回転を実装できます。



四元数機構の「内部キッチン」はあまり明確ではなく、私にとっては興味深いものではありません。そして、あなたが数学者でない限り、それはあなたにとって面白くないかもしれません。また、クォータニオンで動作するライブラリを見つけて、問題を解決しやすくすることをお勧めします。



BulletまたはBlender数学ライブラリは、開始するのに適した場所です。