はじめに
Bo_bdaの同僚は、画像処理と分析の基本的な問題について話します。 まあ、私は側にとどまることができず、私の経験を共有することはできません。 今日は、マルコフネットワーク（外国文学のマルコフランダムフィールド）などの興味深いことについて説明します。 この数学的モデルは、グラフィックス処理のほぼすべてのタスクを解決するために使用されます（ここでは、セグメンテーション、画像復元、ステレオイメージング、3Dのさまざまな質問などが必要です）。
注意！ 大量の写真の下（グラフィックスに関するブログ投稿は、それが何のためであるかです）。
問題の声明
原則として、直接タスクと逆タスクの2種類のタスクがあります。 たとえば、直接的なタスクはコンピューターグラフィックスで解決されることがよくあります。光源のセット、環境パラメーターを入力に与え、出力でシーンモデルを取得します。 コンピュータービジョンでは、すべてが正確ですが、その逆も同様です-一連の画像をフィードして、対象に興味がある場所を見つけます（機械学習では、非常に似た意味を持つ概念があります- 回帰 ）。 より正式には、問題は次のように定義できます。特定の値のセットに対して、未知のモデルのパラメーターを計算する必要があります。
具体的には、次の問題を解決してみましょう。必要なオブジェクト（赤いストローク）と他のすべて（それぞれ青）をマークできる場合は、上の写真のヒトデを選択します。
理論的背景
そのため、ストロークを使用して、特定の条件を満たす任意のポイントセットをマークしました。
統計的推論は、その部分に基づいてサンプル全体に関する情報を取得すると呼ばれます （ wiki ）。 頻度とベイジアンの2つの主なアプローチがあります。 後者を使用します。なぜなら、それは私たちにとって非常に興味深く有用な概念、つまり先験的な確率によって操作されるからです。
pの特定の値の事前確率分布は、実験データ（ wiki ）を考慮する前にpについての仮定を表す確率分布です。 それが私たちの条件に非常に適しているとは思いませんか？ :)
数学的統計の尤度関数は、パラメータ関数（ wiki ）と見なされるパラメトリック分布からのサンプルの共同分布です。
事後最大値 （最大事後確率-MAP）を推定すると 、事前確率分布（ wiki ）を使用して特定の値を計算できます。
要点をつかむ
探している変換は次のように説明できます。
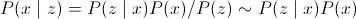どこで
P（x | z）-事後確率（ wiki ）;
P（z | x）は尤度関数です（データ、つまり現在の画像に依存します）。
P（x）-事前確率（データに依存しない）。
実際、最適な分離を見つける問題は次のように定式化できます。
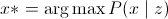（これは式であり、MAPを表します）、または、同じもの
どこで
E（x）-画像エネルギー。
各部分を個別に検討してください。
尤度関数
x = 0またはx = 1のこの関数は、現在のピクセルzが画像の目的の領域に属するかどうかを示します。 右の図でそれを見ることができます。
結果を改善するには、最大値を見つける必要があります。
結果は次のようになります。
事前確率
このパラメーターを使用すると、セグメント化時に隣接ピクセルを考慮することができます。 現在のピクセルを隣接するピクセルと垂直および水平に接続します。 次に：
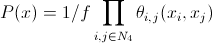どこで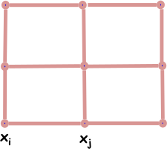 
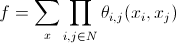-分離機能;
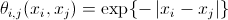-「事前優先」（ yurivのプロンプトでの事前確率）。
同時に、みんな
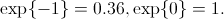
事後確率
この用語を決定する際に、ギブス分布（ wiki ）を使用します 。
どこで
-画像のエネルギー。最初の項は現在のピクセル自体のエネルギー値であり、2番目は隣接ピクセルとの合計値です。 wは特定の重みであり、その値は実験的に決定されます。
-尤度関数;
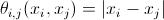-事前確率。
少しだけ残っていますが、これが最も重要なことです。
エネルギー最小化
最初に確立したように、最小エネルギーはMAPに対応します。 この場合：
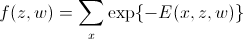
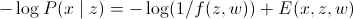
（最小エネルギーを求めた）
結果
「それは何であり、最も重要なのは、なぜ？！」と読者は尋ねます。 重みwの異なる値を示す結果は次のとおりです。
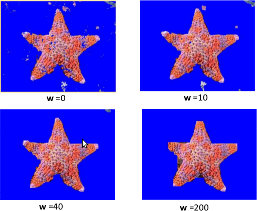
結論
この方法の特別な魅力は、エネルギー式を設定できることです。 たとえば、直線のみの画像、特定の数の直線/曲線の交点などを選択できます。 ところで、MS Office 2010の幸運な所有者は、説明されている技術を感じることができます。 背景除去ツールを使用するだけです。
ご清聴ありがとうございました！
コピーライターコーナー
使用されているすべての画像は、Carsten Rotherのものです。 数式は、オンラインラテックスインタープリターを使用して作成されます。
真面目な文学のリスト
- カルステンロザー作品
- リチャード・セリスキコンピュータビジョン：アルゴリズムとアプリケーション