注釈
1、2、3、4、5。 私たちは遊びを隠そうとします。 この記事では、バイナリイメージ上のオブジェクトをマーク（またはカウント）するアルゴリズムと、追加のパスなしでこれらのオブジェクトの幾何学的特性を計算する方法について説明しています（まだ公開されていないパート2）。 このタイプのアルゴリズムは、バイナリ準備のパターン認識でよく使用され、計算効率を示します。
記事の最後に、読者に興味深い問題が提示されます。アルゴリズムの実際の実装において、有能な解決策が存在し必要です。 ソースコードは提供されていますが、以前の投稿とは異なり、MatLab言語ではなく、完全に無料で劣らず強力なSciLab環境で実行されました。
はじめに
リアルタイムで使用するために設計された実際のアプリケーションでは、パターン認識は多くの場合、次のシーケンスの形式で実行されます。
画像取得（1）->適応二値化（2）->一連の形態学的操作（3）->オブジェクトのマーキング（4）->オブジェクトの特徴の空間の充填（5）。
図1-画像上の単純化されたパターン認識パターン。 このスキームは、特徴空間を分割して決定を行うステップを排除します。
図2は、2値化後の画像の断片と一連の形態学的操作（図2a）および実際のマークアップ結果（図2b）を示しています。
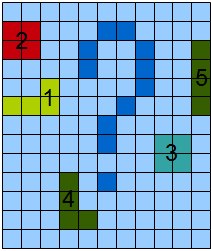
図2 -a）は2値化された画像、b）はマークされたオブジェクトを含む画像です。
この記事では、オブジェクトにマークを付けるだけでなく、面積や境界などの幾何学的特性も計算します。 それらの関係は、オブジェクトのコンパクトさとマリノフスキーフォームファクターを記述し、より複雑な幾何学的特徴、伸び、輪郭の特徴と組み合わせて表現できます。
科学的に、取得したいものは、接続されたエリアの割り当てと呼ばれます 。 この問題には多くの解決策があります-テンプレート[1]、いくつかの再帰的実装（たとえば、[2]のリスト1）などに基づきます。
無効なラベリング（BIT * img []、 int * labels []）
{
int L = 1;
for （ int y = 0; y <H; ++ y）
for （ int x = 0; x <W; ++ x）
塗りつぶし（img、labels、x、y、L ++）;
}
void Fill（BIT * img []、 int * labels []、 int x、 int y、 int L）
{
if （（labels [x] [y] == 0）＆（img [x] [y] == 1））
{
ラベル[x] [y] = L;
if （x> 0）
塗りつぶし（img、labels、x-1、y、L）;
if （x <W-1）
塗りつぶし（img、labels、x + 1、y、L）;
if （y> 0）
塗りつぶし（img、labels、x、y-1、L）;
if （y <H-1）
塗りつぶし（img、labels、x、y + 1、L）;
}
}
*このソースコードは、 ソースコードハイライターで強調表示されました。
リスト1-接続されたドメインのマークアップアルゴリズムの再帰的な実装。
これはすべて私たちに適していません。
この領域の各ピクセルに同じ領域の隣接ピクセルが存在する場合、ピクセルドメインは接続と呼ばれます。 接続の種類については、 このトピックで図を示しました（図1,2）。 アルゴリズムは4つ接続されますが、精神的な労力をあまりかけずに、8つの接続されたバリアントに対してやり直すことができます。
ワンパス、非再帰的マークアップアルゴリズム
このアルゴリズムのアイデアは、図3に示されているコーナー（ABCマスク）の使用に基づいています。
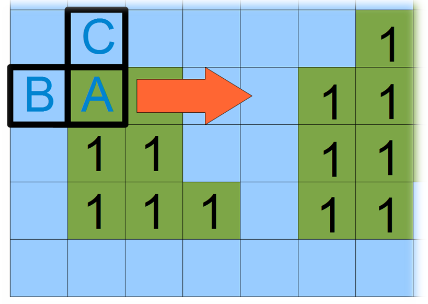
図3 -ABCマスクと連続画像スキャンの方向。
このマスクの画像の通過は、左から右、上から下に行われます。 画像の境界を超えるオブジェクトは存在しないと考えられるため、BまたはCがそこにある場合、スキャン中に追加の検証が必要になります。 図4は、画像内の5つの可能なマスク位置を示しています。
それらを考慮してください。
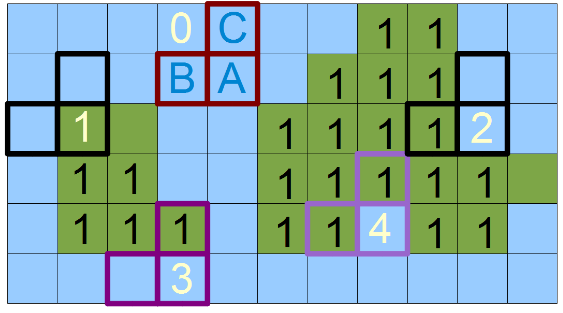
図4 -ABCマスクの5つの可能な位置
- マスクの3つのコンポーネントすべてがマークされていない場合、番号0に配置します。この場合、ピクセルをスキップします。
- 要素Aのみがマークされている場合、番号1に配置します（この場合、新しいオブジェクトの作成について説明しています）。
- 位置番号2、要素に要素Bのマークが付けられている場合-この場合、現在のピクセルAにBにあるラベルを付けます。
- 要素が要素Cとしてマークされている場合、3番目の位置に配置します。この場合、現在のピクセルAをCにあるラベルでマークします。
- 番号4の位置は、ラベル（オブジェクト番号）BとCが接続されている、つまり、同等であり、ピクセルAがBまたはCとしてラベル付けできることを意味します。一部の実装では、そのようなラベルの等価グラフが作成され、しかし、私の意見ではこれは必要ありません。 そのようにします-BがCに等しくない場合 、ラベルBでCとしてマークされているすべての処理済みピクセルの番号を付け直します。しかし、それについては最後に詳しく説明します。
実装により近い。
まず、図2に示されているものと同様のテストデータ、つまり0と1で構成される画像行列を作成します。
画像= [0 0 0 0 0 0 0 0 1 0 0 0;
0 0 0 1 1 0 0 1 0 0 0;
0 0 0 1 1 0 0 1 1 0 0;
0 1 1 1 1 0 0 1 1 1 1;
0 1 1 1 1 0 0 0 0 0 0;
0 1 1 1 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 1 1 0 0;
0 0 0 0 0 0 1 1 1 0 0;
0 1 1 0 0 1 1 1 1 0 0;
0 1 1 0 0 1 1 1 1 1 1;
0 1 1 1 0 1 1 0 1 1 0;
0 0 0 0 0 0 0 0 0 0 0 0 0]]
Matplot（Image * 255） //絵のようにマトリックスを見てみましょう
[m、n] =サイズ（画像）; //マトリックスの水平方向と垂直方向の寸法を調べます
km = 0; kn = 0; //引き続き有用です
cur = 1; //オブジェクトをカウントするための変数
*このソースコードは、 ソースコードハイライターで強調表示されました。
リスト2-ソースデータの初期化。
そして、一連の単純で明白なチェックを実行してイメージを調べます。 写真を通過するABCマスクを図3に示します。このマスクでチェックされる可能な組み合わせを図4に示します。
//画像ピクセルのサイクル
i = 1：1：mの場合
j = 1：1：nの場合
kn = j-1;
kn <= 0の場合
kn = 1;
Bは0です。
他に
B =イメージ（i、kn）; //記事の図3を参照
終わり
km = i-1;
km <= 0の場合
km = 1;
Cは0です。
他に
C =画像（km、j）; //記事の図3を参照
終わり
A =画像（i、j）; //記事の図3を参照
if A == 0 then //現在のピクセルが空の場合、何もしない
elseif B == 0＆C == 0 then //ピクセルの周りが空で空でない場合-これは新しいオブジェクトについて考える機会です
cur = cur + 1;
画像（i、j）= cur;
elseif B〜= 0＆C == 0 then
画像（i、j）= B;
elseif B == 0＆C〜= 0 then
画像（i、j）= C;
elseif B〜= 0＆C〜= 0 then
B == Cの場合
画像（i、j）= B;
他に
画像（i、j）= B;
画像（画像== C）= B;
終わり
終わり
終わり
終わり
*このソースコードは、 ソースコードハイライターで強調表示されました。
リスト3-画像ピクセルの連続スキャンと接続領域のマークアップ。
このスクリプトの結果は、ラベル付きマトリックスになります。
図5-リスト2および3の結果-オブジェクトには一意の番号が割り当てられます。
欠点は、番号が連続していないことですが、概してそれは絶対に必要ではありませんが、アルゴリズムの追加の修正によって修正されます。
記事の最初の部分の結論として、特別な構造へのポインターのマトリックスがインテリジェントに使用される場合、ラベルの番号付けを完全に省略することができます。 これについては、読者に反省することを提案します。 SciLabでポインターを使用してバージョンを実装することはできませんが、記事の最後の3部では、擬似コードを使用してこれを行います。
第二部で何が起こるか-それは、オブジェクトの形状、コンパクトさ、マリノフスキー因子の経験的要因について話します。 私が現在取り組んでいるユニークなイラストが表示されます。このイラストでは、オブジェクトの形状の滑らかな変化が、因子形式の増減によって反映されます。
読んでくれて、フィードバックを待っているすべての人に感謝します。
参照と参照
[1]アルゴリズム/画像リンク内のオブジェクトのカウント（明らかに、この記事はかつてHabréについてでしたが、見つかりませんでした）
[2]講義： pptファイルへの画像リンクに含まれる情報の分析