
略語の規則によれば、タイトルはそうではありませんが、略語を描いたらタイトルを注釈に変えます。 だからここに...
- BINS-ストラップダウン慣性ナビゲーションシステム
- UAV-無人航空機
- OCH-センサーの感度軸
この記事では、OChセンサーが非直交に向けられているナビゲーションシステム、つまり UAVに関連付けられている座標系の軸に対してゼロ以外の角度で配置されています。 このようなSINSの特徴は、各センサーからの情報に応じて、オブジェクトの角速度(ジャイロスコープの場合)および線形加速度(線形加速度計の場合)の3つの成分すべての値を取得できることです。
この記事は、マルチコプターの構築、パート2への追加として書かれています。 目標は、安価なセンサーでゼロドリフトに対処する方法の1つを説明することです。
はじめに
SINSの利点は、その比較的安価(「低コスト」カテゴリのセンサーを使用できること)、小さな寸法と重量、および低消費電力です。 これらの利点は、マイクロメカニカルナビゲーションセンサー(ジャイロスコープ-MMG、加速度計-MMA)上に構築されたSINSで特にはっきりとわかります。
線形マイクロメカニカル加速度計のブロックは、慣性航法システムの一部として、移動する物体の見かけ上の加速度のセンサーとして使用されます。 それらには高精度の特性はありません(安価なMMAを考慮する場合)。 ただし、適切なタスクがあります。 たとえば、小型航空機では、MMAユニットの低消費電力と相まって、サイズと重量が小さいため、多くの利点があります。 同じことは、衛星システム(GPS、GLONASSなど)と統合されている自動車産業にも当てはまります。
低コストのマイクロメカニカルセンサーの深刻な問題の1つは、ランダムドリフトのゼロです。 簡単に言えば、ドリフトとは、物体が回転していることをセンサーが示すとき(MMGドリフト)のことですが、実際には回転はありません。 ドリフトには、補償可能な一定の成分と、補償が困難なランダムな成分があります。 ランダムエラーを処理する方法はいくつかあります。 その1つは、情報の冗長性を備えた非直交SINSの構築です。
この記事では、4つの2軸MMA ADXL-203CEのブロックの例を取り上げます。そのOFは2つのコーンのジェネレーターと平行に配置されています。 一軸メーターの半円錐角の最適な角度は54.75度です[1] 。 2軸センサーの場合、2つのコーンにOFPのレイアウトを適用する必要があります。 このような設計は、RF特許第1810299「過剰な構造を持つ慣性感応素子のブロック」に記載されています。
オーバーブロック
情報の冗長性を作成するには、ブロック内の測定チャネル(感度軸)の数が、測定されたパラメーターの数よりも大きいことが必要です。 4つの2軸センサーのブロックには、8つの測定チャネルがあり、通常のSINSを構築するのに十分です。 この場合、前述のように、OChセンサーはコーンの母線と平行に配置する必要があります。 このような構造を作成するために、円錐やピラミッドを作成する必要はありません。 センサーは、ボックスの側面に配置し、側面の法線を中心に回転させることができます。 以下を入手してください
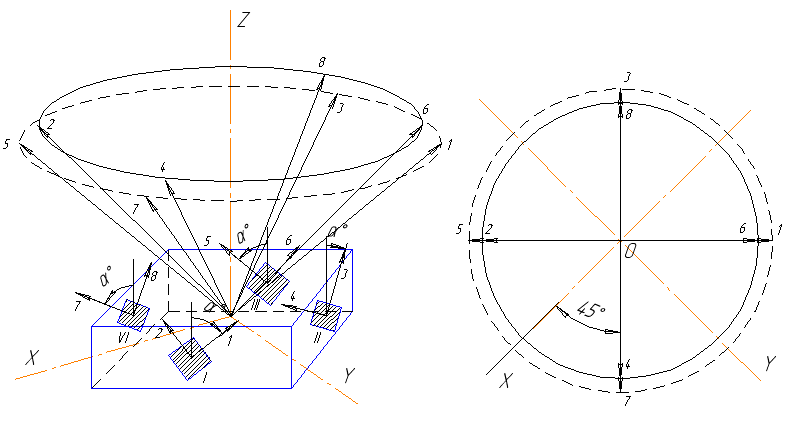
図 1.冗長ブロックの設計。
センサー自体は、取り付け穴付きのミニボードに既にはんだ付けされて販売されています。 ブロックのベースは、テキソライト(プラスチック、木材など)で作成できます。 ベースの取り付け穴の精度は二次的な役割を果たします。 センサー自体の場合、内部の方向誤差は非常に大きくなります。 このようなSINSを組み立てた後、いずれの場合も、センサーを較正して、ガイド余弦およびスケール係数のマトリックスの実際の値を決定する必要があります[2] 。
センサーのこの方向については、ガイド余弦のマトリックスを構成する必要があります。 この行列は、接眼センサー(行)とオブジェクト座標三面体(列)の軸の間の角度の余弦で構成されます。 ガイド余弦の行列を構築するには、連続回転の方法を使用できます[ 3、4 ] 。
上記のセンサーを設置すると、次の回転スキームが得られます。
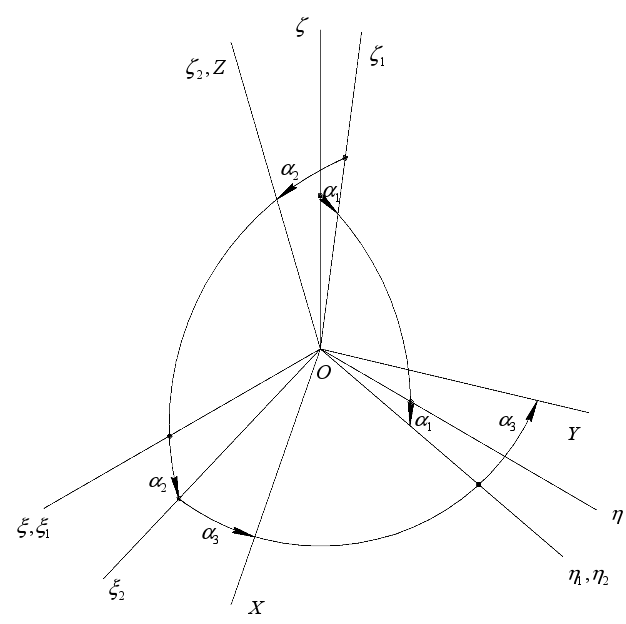
図 2.ブロック内のセンサー回転の図
この場合、結果は行列[8x3]-センサーの感度の8軸と関連する座標系の3軸です。 ガイドコサインのマトリックスのコンパイルの正確性を検証するには、いくつかの基準があります。
- 行列Hの行ベクトルのノルムは1です
- 3本の線はいずれも直線的に独立しています(ブロック内に2つの平行および3つの同一平面上のOChがないという要件)
- 行列(H T * H) -1は誤差の共分散行列であり、対角要素は1より小さくなります。
眼球の最適な向き(半角が54.75度の1つの円錐の表面)については、次のようになります。

これは、OCの所定の方向に対して、OX軸とOY軸に沿った誤差分散が2の根に、OZに沿って半分[1]減少することを意味します。
冗長ブロック情報の処理
最も単純なケースでは、絶対角速度ベクトル(または見かけの加速度)の成分の推定値を取得するには、線形代数方程式(SLAE)のシステムを解く必要があります。ガイド余弦のマトリックス。 情報の冗長性により、取得されたSLAEは過剰に決定されます(方程式の数は変数の数よりも大きくなります)。 一般的な場合、そのようなソリューションのシステムには(正確な)ソリューションはありません。 おおよその解決策として、たとえば、最小二乗法のガウス法の単純なアルゴリズムを使用できます。

この式を使用して、長方形行列の擬似逆行列が計算されます。 この方法は、抑制されたノイズに重大な制限を課します(ゼロ平均、ガウスノイズ、異なる測定チャネルでのノイズの均等分散)。
もう少し複雑なアルゴリズムは、ガウスマルコフ最小二乗法(重み付き最小二乗法、MVNC)です。

ここで、Nはガイド余弦の行列、
Cは、測定ノイズの共分散行列です。
再帰的なガウスマルコフ最小二乗法は、MVNCから派生します。MVNCは、 [5]でカルマンビュシーフィルターと呼ばれます。


このアルゴリズムは、センサーの動的モデルを考慮しません。
次のアルゴリズムは、センサーのダイナミクスを考慮したカルマンフィルターです。


マニュアル[5]では、これらのアルゴリズムの詳細が説明されていますが、さまざまな特殊なケースのノイズに対するカルマンフィルターの一般化、集約システム「ブロック-観測装置」のスキームもあります。
最小二乗法に基づくアルゴリズムに加えて、たとえばニューラルネットワークを使用して方程式系を解くことができます[ 6 ]
ブロックキャリブレーション
アナログ出力のセンサーを使用する場合は、センサーのスケール係数を調整して、ボルトを角速度と角速度にする必要があります。 デジタル出力を備えたセンサーの場合(たとえば、アナログデバイスにはSPIインターフェイスを備えたマイクロメカニクスがあります)、スケール係数を較正する必要はありません。 また、ガイド余弦のマトリックスをキャリブレーションする必要があります。 すでに取り付けられたユニットの方向角の実際の値を決定します(「膝の上」のベースは正確に製造できません。さらに、キャリアボード上のセンサーのはんだ除去の誤差と内部の欠陥)。 センサーのノイズが非常に大きい場合、キャリブレーションに煩わされても意味がないと思われるかもしれません。 ただし、キャリブレーションにより、平均ノイズバイアスは除去されます。 したがって、キャリブレーションは依然として重要です。
調整方法 加速度計のブロックの場合、これは地球の重力場で行うことができます。 ジャイロスコープについても、その場所での惑星の回転の垂直成分がわかっている場合。
卒業証書に取り組むとき、冗長ユニット、ADC、PC、およびターンテーブルで構成される実験室のセットアップを使用しました。

ここでの主な難点はターンテーブルです。 このデバイスはYoung Techniqueでは販売されていないと思います。 また、高速道路から遠く離れた場所にある「アンティード」基盤上に「ミニ研究室」を組織することをお勧めします。 マルチコプターの構築、パート2で述べたように、MMAは非常に敏感です。 ブロックが置かれているテーブルを「さらさら」すると、出力信号のグラフを肉眼で確認できます。
スケール係数のキャリブレーション方法は次のとおりです。
- さまざまな角度(解像度、たとえば15度)でセンサーを使用してボードを固定するために、ベースの端にいくつかのグループの穴を開けます。
- センサーが最大の正の値を与えるようにベースを水平線に設定します(センサーが信号のゼロオフセットを使用する場合は、最大値のみ)
- 顔の法線を中心にセンサーを15度回転すると、最大値から最小値まで(+1 gから-1gまで)の値が得られます。
得られた測定値に基づいて、傾きがスケール係数となる傾向線を簡単に作成できます。 ただし、ゼロに近いセンサーの読み取り値はトレンドからさらに逸脱することを考慮する必要があります。
ガイド余弦のマトリックスの賢明なキャリブレーションには、回転テーブルが望ましい。 存在しない場合は、キャリブレーションされたセンサーを備えたMMAブロックの面をローカル座標三面体の3つの平面すべてにできるだけ垂直に配置し、センサーの読み取りに基づいて、ベースエッジの角度を決定する必要があります。 ベースがボックスであると確信している場合、タスクはいくらか単純化されます。
数学的な考え方を持つ
結論
非直交性と冗長性の影響は何ですか? なぜなら 正または負のランダムなドリフトに苦労しているため、オブジェクト座標軸上のドリフトの投影を合計すると、(もちろん、最適な向きで)総測定ドリフトが減少します。 効果は、コーン軸に沿って1つのOChを向けることで強化できます(奇数の測定チャネルに適しています)。
もう1つの重要な効果は、センサーの数が多すぎることによる信頼性の向上です。 測定チャネルの故障は、測定エラーの増加につながります(ユニットで4つ以上の測定チャネルが動作している間)。 したがって、起こりうる誤動作に適応するアルゴリズムを構築することが可能です。 障害が発生した場合、アルゴリズムを変更する(ガイド余弦のマトリックスを再構築する)必要さえなく、障害のあるチャンネルのMVNKとFCの共分散マトリックスに分散を設定するだけで十分です。
参考文献
1. Vodicheva L. V.過度の測定回数でストラップダウン慣性測定ユニットの信頼性と精度を向上させる//ジャイロスコープとナビゲーション。 1997. No. 1.-S. 55-67。
2. Aleshkin M.V. 測定ユニット/V.Vの冗長情報を処理するための数学モデル、方法、アルゴリズム Aleshkin、AC Matveev、M.V。 Aleshkin //インターネットとイノベーション:インターンの作品のコレクション。 conf。 サラトフ:SSTU、2008.S。377-380。
3. ターンのスキーム
4. n次元空間を有効にする
5. Brammer K.、Ziffling G. Kalman-Bucyフィルター。 確定的観測と確率的フィルタリング
6. ニューラルネットワーク。 非線形方程式系の解