Wolfram Mathematica：知人

Wolfram | Alphaを知っている人なら誰でも、Wolfram Mathematicaについて聞いたことがあるでしょう。 残念ながら、検索ではHabréにこの素晴らしい環境に関する投稿がないことが示されました。この記事では、Mathematicaでのプログラミングに特化した一連の出版物を開きたいと考えています。 そもそも、このシステムの機能には多くの特徴がありますので、ご説明ください。しばらくお待ちください。 この数学的パッケージがhabrazhiteliにとって興味深いものである場合、他の記事が確実に続き、より具体的に、環境と内部言語を扱う方法を教えます。



Mathematicaは、多くのプログラミングパラダイム、高度なデバッグツール、自動インターフェース設計などをサポートする柔軟な記号言語に基づいています。 設計から実装までの開発プロセス全体を簡素化します。 Mathematicaのすべて-データ、プログラム、式、グラフ、ドキュメント-はシンボリック式の形式で表されます。





数学環境について説明するため、まず第一に、その計算能力とタスクの範囲について話す必要があります：Mathematicaには、Wolfram Researchによって発見された高度に最適化されたアルゴリズムの世界最大のコレクションが含まれています。 JIT（オンザフライでのコンパイル）の有効性と自動構成可能な並列コンピューティングの組み合わせにより、回答の正確性と受信の高速性が保証されます。 システムはあらゆる精度の数値をサポートしており、結果の品質を改善するために内部計算にさらに正確な値が使用されることがよくあります。 また、精度を高めるために、環境は記号計算を使用します。 式を単純化または変換しようとし、数値計算を実行します。 この場合、解法アルゴリズムは数千の方法から自動的に選択され、計算プロセス中にも変更できます。これにより、解法の速度が上がり、手動タスク設定よりも精度が向上します（ただし、これは禁止されていません）。





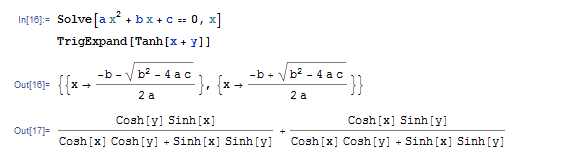
数学的な可能性はすべて、線形システムだけでなく、代数的、微分的、反復的、機能的等式および不等式を解く能力を提供する強力な関数の小さなセットに含まれています。 微分および積分分析、級数分析とフーリエ分析、クラスター分析、積分変換などを実行する機能。 また、シンボリックマトリックス、任意の精度の数を持つマトリックス、高密度、スパース、数百万の要素を持つマトリックス、代数方程式の根とシステムを見つけるためのさまざまな数値手法。 Mathematicaは、離散コンピューティングのための包括的なシステムを提供し、因数分解と分解、構造演算、多項式の除算など、多項式代数のすべての側面を含みます。 この環境では、ベジェ曲線、Bスプライン、NURBS曲線、およびサーフェスを任意の数の次元で作成、表示、管理できます。 スプラインを使用してデータを補間すると、任意のフィールドにスプラインメソッドを適用できます。





単純で多次元の積分、およびそれらのシーケンスの和と積を取ります。 多数の数値積分法がサポートされています。 噂によると、Mathematicaは既知のすべての積分の99％を取り、この分野のリーダーです。 残念ながら、現時点ではそのような情報をサイトで見つけることはできませんでしたが、この分野で私を失望させることはありませんでした。





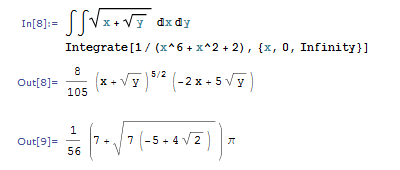
Mathematicaはグラフの幅広い基本的な操作とアルゴリズムをサポートします。たとえば、パス、ループ、クリックなどの検索です。 任意のグラフを設定し、ランダムグラフを生成し、インタラクティブに設計し、標準のグラフ形式とマトリックスビューにエクスポートおよびインポートすることもできます。 素因数分解、素数、比較およびモジュラー算術などの単純なことについては言及することさえできません。 任意の精度の数学定数が利用可能であり、πやeなどの定数の数百万の文字が瞬時に計算されます。





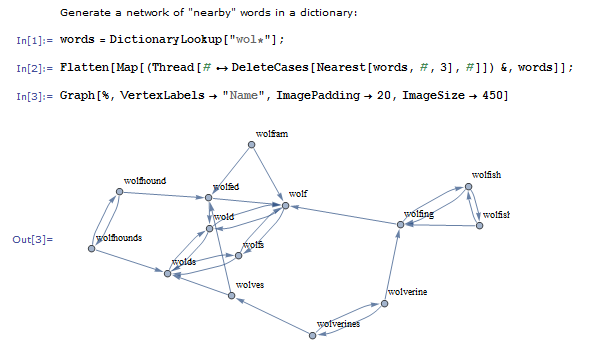
統計学者は、 他のどのシステムよりも多くの統計分布が含まれており、統計的な測定と操作の完全なセット（数学的期待値と分散からセミオプションと情報のエントロピーまで）、自動パラメーター推定と仮説検定、統計モデルの分析などを提供します。





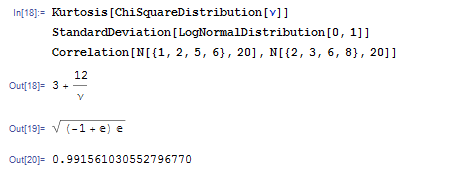
Mathematicaは強力なコンピューティング環境であるだけでなく、計算生物学や金融工学から波動解析や地理情報システムまで、活動の多くの技術分野に影響を与える組み込みの追加機能を備えています。





Mathematicaは、スプレッドシート、xml、2次元および3次元のグラフィック形式、マルチメディアファイル、pdfやhtmlを含むドキュメント、アーカイブおよびその他の多くの特定のデータ形式を含む、インポートおよびエクスポート用の数百の形式をサポートしています。 最初は、gif、jpeg、png、svg、eps、avi、flv、quicktime、swfなど、すべての標準のラスター、ベクター、およびビデオ形式がサポートされています。 ビデオファイル全体をインポートし、さらに処理するために個々のフレームを選択できます。 また、画像を操作するために、Mathematicaには、画像を取得したり、さまざまなフィルター、セグメンテーション、形状分析、アウトライン選択などを適用したり、リアルタイムで機能する多くの機能が組み込まれています。





マルチコアシステムでは、環境が計算のいくつかの部分を同時に自動的に開始します（いくつかは魂がねじれていますが、少し手を加える必要があります）。 パラレルコンピューティングサブシステムは、ネットワークコンピューティング、グリッドシステム、クラウドコンピューティングに合わせて拡張でき、シンボリック言語はデータ分離の多くのモデルをサポートします。 このシステムでは、GPUをプログラムすることもできます：CUDAおよびOpenCLの組み込みサポート。 すべてのGPU操作は、プロセス間のデータ交換、自動コンパイル、GPUコードのリンクなど、環境に完全に統合されています。





Mathematicaには、構造化および非構造化データを2dおよび3dで表示するための完全な関数セットが含まれています。 等高線および密度グラフ、ポイント、ラインおよびサーフェスからのグラフ、ベクトルグラフおよび流線のグラフ、ヒストグラム、2次元および3次元のセクター図および列図、バブル図、専門分野のグラフ（財務および統計、グラフ理論など）を表示する機能が組み込まれています、制御システムなど：チャート「日本のローソク足」、QQ正規確率チャート（分位点プロット）、「口ひげのある箱」（箱ひげ図）、LAFCH（ボード線図）など。





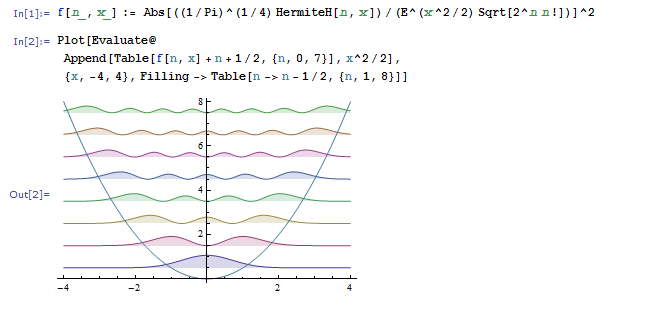
グラフィックスサブシステムは、関数、データ、図、画像、または注釈の高品質の静的または動的表現を提供し、計算の速度と視覚的な対応のバランスを自動的に決定します。 グラフィック機能は、印刷領域と地域化を個別に選択できます。 Mathematicaには、画像サイズ、軸ラベル、グリッド表示、分割、塗りつぶし、3Dライティング、カメラアングルなど、ディスプレイのあらゆる側面を制御する数百のオプションが用意されており、プロ並みのグラフィックを作成できます。 さらに、3Dグラフィックはインタラクティブで、カメラの設定をリアルタイムで変更できます。





これとは別に、インターフェイスの自動設計、シンボリック制御要素、単一の入力インターフェイス、さまざまな種類のブレークポイントを設定する機能を備えたデバッグとプロファイリング、コード実行中の式の監視、プログラム実行の視覚的な段階的な制御などにより、開発について言及する価値があります他の人に。 Mathematicaは、構文の強調表示、エラー報告、コマンドの追加、自動フォーマット、インデントなどを備えた強力なソースコードエディターを提供します。 多言語IDE Wolfram Workbench（Eclipseベース）との統合により、プロジェクトファイル管理、ソースコードを操作するための高度なツール、デバッグ、構文解析など、開発効率を高めるさまざまなツールにアクセスできます。





Mathematicaには、ボタンとスライダー、タブ、チェックボックス、ポップアップメニュー、ダイアログボックス、ツールバーなどのインターフェースと制御要素の完全なセットが含まれており、独自の要素を作成する機能も提供しています。 システムは各プラットフォームに対して自然な方法でコントロールをレンダリングするため、どのOSで動作するかを考える必要なく、グラフィックアプリケーションを自由に共有できます。 ユーザーインターフェース要素にはMathematica式を含めて表示できます。





システムを使用すると、パッケージを作成できます。プラットフォームに依存しないコードライブラリを使用すると、パッケージを再利用し、ドキュメントと補助ツールバーの完全なセットで簡単に配布できます。 外部コントローラーや入力デバイスをMathematicaに簡単に接続できます。ゲームパッド、ジョイスティック、触覚デバイス、3Dマウス、その他のHIDデバイスを自動的に認識して設定できます。





環境での作業は、主にいわゆる「ラップトップ」（ノートブック、* .nb）で行われます。これには、フォーマットされたテキスト、グラフィック、対話型アプリケーション、コードおよびデータを含めることができます。また、レポートまたはプレゼンテーションの形式で配布することもできます。 数式の入力は非常に簡単であり、同時に非常に強力です。 システムには高品質のワードプロセッシングシステムの一般的な機能がすべて含まれており、ドキュメントの基礎となる文字構造はカスケードスタイルシートを設定するための柔軟なオプションを提供します。メニューおよびプログラムの両方で1000を超える書式設定およびデザインオプションを使用できます。





Mathematicaは任意の標準SQL-DBMSに接続し、従来の文字列SQLクエリの完全サポートとともに、データベース、クエリ、結果の高レベルのシンボリック表現を提供します。 サブルーチンを呼び出すことができ、C、.NET、Java、その他の言語のプログラムから呼び出すことができます。 個々のプロジェクトで使用したり、ライブラリや実行可能ファイルにコンパイルしたりするためのCコードを自動的に生成します。 実行時に動的ライブラリを接続します。 WSDL Webサービスに接続します。 これらはすべて、既存のインフラストラクチャに簡単な実装を提供します。 webMathematicaは、最新のWeb標準とサービスを使用して動的コンテンツを追加し、Web経由で計算を実行するインタラクティブなWebサイトの形で高性能のMathematicaアプリケーションを展開します。 gridMathematicaを使用すると、自動調整とプロセス制御を備えたクラスターでアプリケーションを並行して実行できます。 ソフトウェアレポートは、PDF、スプレッドシート、HTML、RTFなど、さまざまな形式でサポートされています。





強力な操作機能のおかげで、無料のMathematica Playerを使用して任意のシステムで表示および実行できるインタラクティブなガジェットを作成できます。 パッケージのバージョン8の機能の中で、Wolfram | Alphaデータへの直接アクセスと自由形式の言語入力を選択できます。 簡単な人間の言語で式を入力できます。これは初心者に役立つ場合があります。





上記からわかるように、システムはクロスプラットフォームであり、Windows、mac os、linux、さらにはsun solaris 10（32ビット版と64ビット版の両方）向けにリリースされています。 （ システム要件とサポートされているOSの正確なリスト）。 そして、もちろん、そのような強力なシステムでは、ドキュメントなしではできません。 Mathematicaはここでも失望しませんでした：ヘルプは100,000以上の例を含むインタラクティブなラップトップで構成されています。 すべての例は、ドキュメントで直接実行または変更できます（恐れないで、変更は保存されません）。新しい機能を簡単に習得できます。

おわりに

準備では、公式Webサイトの機能セクションの資料、ドキュメント、および環境に関する長年の個人的な経験を使用しました。 追加情報については、上記のセクション 、 ソリューションセクションのシステムの使用方法に関する情報、およびユーザーストーリーをご覧ください 。 プロ版にはかなりの費用がかかりますが、学生、教育機関、家庭での使用には大幅な割引があります。 試用版も15日間使用できます。 [そして、あなたはどこでそれを知っているあなた自身でそれをダウンロードすることができます]。

興味を持っていただければ幸いです。Habrには、Wolfram Mathematicaに関するさらに多くの記事があります。



UPD： vayunは、学ぶべき最も興味深いことの1つ-Wolfram Demonstrations Projectについて言及しました 。 この プロジェクトでは 、Manipulateを使用して作成された多くのミニプログラムを見ることができます。 すべてのプログラムにはオンラインプレビューがあり、デモプロジェクト（無料のMathematica Playerで起動できます）とソースコードをダウンロードできます。