ここでは、遺伝的アルゴリズムなどのさまざまな最適化アルゴリズムがすでに議論されています。 ただし、多くの自由度を持つ問題で最適なソリューションを見つける方法は他にもあります。 それらの1つ(そして、最も効果的なものの1つ)は、アニーリングをシミュレートする方法であり、ここではまだ説明していません。 この不正を排除し、この素晴らしいアルゴリズムを可能な限り簡単な言葉で紹介すると同時に、単純な問題を解決するための使用例を紹介することにしました。
遺伝的アルゴリズムがとても人気がある理由を理解しています。それらは非常に想像力に富んでおり、したがって理解が容易です。 実際、問題の解決策を提示することは難しくはなく、特定の特性を持つ生き物の集団を開発する実際の生物学的プロセスとして非常に興味深いものです。 一方、アニーリングアルゴリズムには、実世界で独自のプロトタイプもあります(名前からも明らかです)。 確かに、彼は生物学からではなく、物理学から来ました。 このアルゴリズムが模倣するプロセスは、粒子が高温でランダムに移動し、エネルギーが最も低い場所で徐々に減速して凍結する、冷却および凝固中の物質による最小エネルギーの結晶構造の形成に似ています。 数学的な問題の場合のみ、物質の粒子の役割はパラメーターによって実行され、エネルギーの役割はこれらのパラメーターのセットの最適性を特徴付ける関数です。
そもそも、忘れてしまった人たちに、このようなエキゾチックな方法でどのようなタスクを解決しようとしているかを思い出させてください。 多数の変数パラメーターがあるため、正確な解を見つけるのが非常に難しいタスクがいくつかあります。 一般的なケースでは、最小値(最大値)を見つける必要がある関数Fと、パラメーターx1..xnのセットがあり、それぞれがその範囲内で独立して変化します。 パラメータとそれに応じた関数は、離散的にも連続的にも変化します。 このような関数は入力データに複雑な依存関係を持つ可能性が高いことは明らかです。入力データには多くの局所的な最小値がありますが、グローバルな最小値を探しています。 もちろん、徹底的な検索によって問題を解決するオプションは常に残っていますが、それは離散的な場合と非常に限られた入力セットでのみ機能します。 これが最適化アルゴリズムの出番です。
乾燥しないように、この記事の枠組みで解決する問題についてすぐに説明します。 m x lのチェッカーボードを想像してください。 セルの側面は1に等しくなります。 ボード上では、これらのポイントを接続する最小ポリラインの長さが最大になるように、nポイントのこのような配置を見つける必要があります。 通常のミニマックスの問題。 明らかに、この場合、関数Fはポイントの特定の配置の最小ポリラインの長さを考慮し、そのパラメーターはポイントのx座標とy座標です。 2 * nパラメーター。
実際には、アルゴリズム
そのため、システムを特徴付ける関数と、この関数が与えられる座標のセットがあります。 まず、システムの初期状態を設定する必要があります。 このために、ランダムな状態がとられます。 次に、k番目のステップごとに、
- Fの現在の値と最良の値を比較します。 現在の値が優れている場合-グローバルベストを変更する
- ランダムに新しい状態を生成します。 その確率分布は、現在の状態と現在の温度に依存する必要があります
- 生成されたポイントの関数の値を計算します
- 生成された状態を現在のものとして受け入れるかどうか。 この決定の確率は、生成された状態と現在の状態の関数の違い、およびもちろん温度に依存する必要があります(温度が高いほど、現在の状態よりも悪い状態を受け入れる可能性が高くなります)
- 新しい状態が受け入れられない場合、別のものを生成し、3番目のポイントから手順を繰り返します。受け入れられる場合、次の反復に進み、温度を下げます(ただし、多くの場合、長いループを避けるために次の手順への移行が行われます)
ポイントからポイントへの遷移の確率を持つこのような複雑なスキームが必要なのはなぜですか? なぜあなたは、単により多くのエネルギーからより少ないエネルギーに厳密に移動できないのですか? それはすべて、既に述べた局所的な最小値に関するものであり、そこでは解決策が行き詰まる可能性があります。 それらから抜け出し、最小のグローバルを見つけるには、時々システムのエネルギーを増やす必要があります。 同時に、最小のエネルギーを検索する一般的な傾向が残っています。 これが、アニーリングをシミュレートする方法の本質です。
そして再びボード上のドットについて
アルゴリズムの一般的なスキームが明確になったので、ラムに戻りましょう。 Javaでタスクを実装します。 最初に、ドットのあるボードについて説明します。
ボード:
public class Board { private Point[] points; private int N; private int width; private int height; public Board(int n, int w, int h) { points = new Point[n]; N = n; width = w; height = h; } public Board(Board board) { points = new Point[board.points.length]; for (int i = 0; i < points.length; i++) points[i] = new Point(board.points[i].getX(), board.points[i].getY()); this.width = board.width; this.height = board.height; } public int getPointsCount() { return points.length; } public int getWidth() { return width; } public int getHeight() { return height; } public Point getPoint(int index) { return points[index]; } public void setPoint(int index, Point p) { points[index] = p; } }
public class Point { private int x; private int y; public Point(int x, int y) { this.x = x; this.y = y; } public double dist(Point p) { return Math.sqrt((x - px) * (x - px) + (y - py) * (y - py)); } public void move(int dx, int dy, int xBorder, int yBorder){ if(((x + dx) < xBorder) && ((x + dx) >= 0)) x += dx; if(((y + dy) < yBorder) && ((y + dy) >= 0)) y += dy; } public int getX(){ return x; } public int getY(){ return y; } }
点の順序は目的の関数を計算するために重要なので、順序付けられたセットを導入します。
public class Polyline { public Point p[]; public int N = 5; public Polyline(int Num) { N = Num; p = new Point[N]; } public double dist() { double d = 0; for (int i = 0; i < (N - 1); i++) { d += p[i].dist(p[i + 1]); } return d; } }
次に、指定された配列の最小ポリラインを探し、その長さをカウントする関数Fが必要です。
public class MinPolyline { private double bestDist; private Polyline bestMinPolyl; private Board board; public Polyline F(Board b) { N = b.getPointsCount(); board = b; int[] perm = new int[N]; boolean used[] = new boolean[N]; for (int i = 0; i < N; i++) { perm[i] = i + 1; used[i] = false; } bestDist = Double.MAX_VALUE; permute (0, perm, used); return bestMinPolyl; } void permute(int first_index, int[] perm, boolean[] used) { if (first_index == N) { Polyline polyl = new Polyline(N); for (int i = 0; i < N; i++){ polyl.p[i] = board.getPoint(perm[i] - 1); } if (bestDist > polyl.dist()){ bestDist = polyl.dist(); bestMinPolyl = polyl; } return; } for (int i = 1; i < N+1; i++) { if (used[i - 1]) continue; perm[first_index] = i; used[i - 1] = true; permute(first_index + 1, perm, used); used[i - 1] = false; } } }
さて、準備はすべて完了です。 これで、アルゴリズム自体の実装を開始できます。
アルゴリズムの実装
一般的なスキームに戻って、そこで座標と温度に応じて2つの分布について言及します。 何らかの方法で定義する必要があります。 さらに、温度が反復ごとに変化するための法則が必要です。 これらの3つの関数を選択したら、アニーリング方法の具体的な図を作成します。 アルゴリズムには、分布と温度変化の法則によって互いに異なるいくつかの修正があると言わなければなりません。 彼らには、スピード、グローバルな最小、実行の複雑さを見つける保証などの長所と短所があります。
私の仕事では、超高速アニーリングと呼ばれる修正を選択しました。 まず、新しい州の採用の確率分布を決定します。

またはコード内:
h = 1 / (1 + Math.exp(-(minPolyl.F(board).dist()- maxDist) / T));
したがって、関数の最悪の結果(より高いエネルギー)で位置を取る確率は、温度が低く、現在のエネルギーと最適なエネルギーの差が大きいほど小さくなります。 次に、温度低下の法則を確立します。 超高速アニーリングの特徴は、すべての座標の変化が独立して考慮され、各座標の温度でさえも独自に決定されることです。
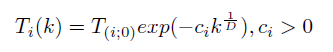
ここで、Dは座標の数(つまり2 * n)であり、kは移動の数です。 ただし、簡単にするために、一般的な温度を引き続き作成します。
T = To * Math.exp(-decrement * Math.pow(i, (double)(1) / (2*(double)N)));
ご覧のとおり、温度は指数関数的に低下し、手順はすぐに終了します。
最後に、新しい座標の分布。 次の値は、1つの座標の相対的な変化を特徴づけます。
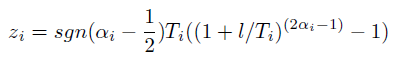
ここで、alphaは区間[0、1]に均一に分布する量です。 新しい座標がその変更のフレームワークに収まらない場合(この場合、ボードを超えています)、計算が再度実行されます。
z = (Math.pow((1 + 1/T), (2 * alpha - 1)) - 1) * T; x = board.getPoint(moveNum).getX() + (int)(z * border);
これで、必要なすべての分布と機能ができました。 すべてをまとめるだけです。 入力データとして、ボードの寸法、ポイント数、初期温度と最終温度、および温度指数の減衰減少を転送する必要があります。
public class AnnealingOptimizer { public int N; public int width; public int height; public AnnealingOptimizer(int n, int width, int height) { N = n; this.width = width; this.height = height; } public Board optimize(double To, double Tend, double decrement){ Board board = new Board(N, width, height); Board bestBoard = new Board(N, width, height); Random r = new Random(); double maxDist = 0; double T = To; double h; MinPolyline minPolyl = new MinPolyline(); for (int j = 0; j < N; ++j){ board.setPoint(j, new Point(r.nextInt(height), r.nextInt(width))); bestBoard.setPoint(j, board.getPoint(j)); } int i = 1; while (T > Tend){ for (int moveNum = 0; moveNum < board.getPointsCount(); ++moveNum){ NewX(board, moveNum, T, width, true); NewX(board, moveNum, T, height, false); } if (minPolyl.F(board).dist() > maxDist){ bestBoard = new Board(board); }else{ h = 1 / (1 + Math.exp(-(minPolyl.F(board).dist()- maxDist) / T)); if (r.nextDouble() > h){ board = new Board(bestBoard); }else{ bestBoard = new Board(board); } } maxDist = minPolyl.F(board).dist(); T = To * Math.exp(-decrement * Math.pow(i, (double)(1) / (2*(double)N))); ++i; } return bestBoard; } private void NewX (Board board, int moveNum, double T, int border, boolean xCoord) { Random r = new Random(); int x; double z; double alpha = r.nextDouble(); z = (Math.pow((1 + 1/T), (2 * alpha - 1)) - 1) * T; if (xCoord){ x = board.getPoint(moveNum).getX() + (int)(z * border); if ((x < border) && (x >= 0)) { board.getPoint(moveNum).move((int)(z * border), 0, width, height); } else { NewX(board, moveNum, T, border, xCoord); } } else { x = board.getPoint(moveNum).getY() + (int)(z * border); if ((x < border) && (x >= 0)) { board.getPoint(moveNum).move(0, (int)(z * border), width, height); } else { NewX(board, moveNum, T, border, xCoord); } } } }
シミュレーテッドアニーリング方法のいくつかの修正は、最適なソリューションを見つける統計的保証を提供することに注意する必要があります。 これは、適切なパラメータを選択すると、アルゴリズムはすべての入力を経由せずに妥当な時間で最適なソリューションを見つけることを意味します。 この実装では、約15,000回の反復で12x12ボードと5ポイントの答えが見つかります。 配置オプションの総数は12 ^ 10であることを思い出させてください。 明らかに、パラメーターを調整することの難しさは利益に値します。 ところで、速度と精度の点でアニーリングする方法は、少なくとも遺伝的アルゴリズムに負けませんが、多くの場合そうです。
最後に、アルゴリズムの視覚的な結果。
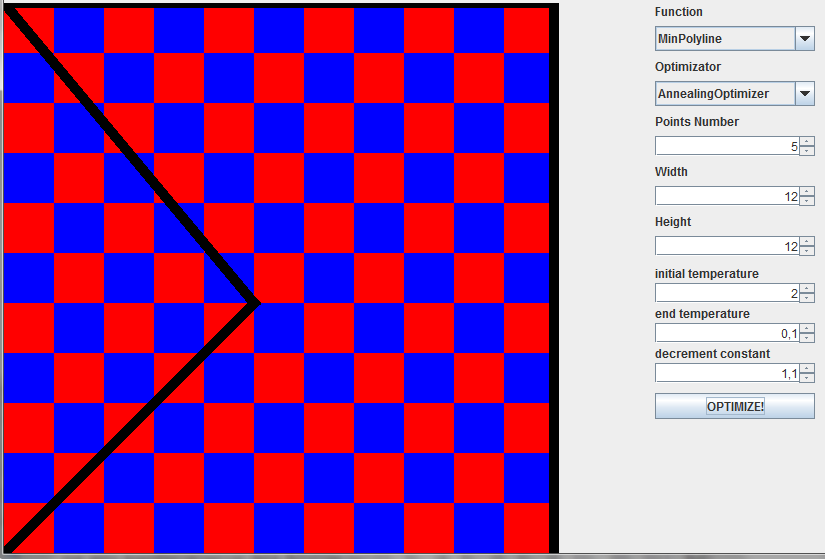
使用された文献:
A.ロパチン「アニーリング法」