ブルームフィルター

こんにちは！ 今日は、ブルームフィルターについてお話します-そのシンプルさに優れたデータ構造です。 実際、このフィルターは、要素をセットに追加することと、要素がセットに属するかどうかを確認することの2つの操作だけで確率セットを実装します。 「この要素はセットに属しますか？」という質問に対する最後の操作が「はい/いいえ」の形ではなく「可能/いいえ」の形で答えを与えるため、セットは確率的です。

フィルターはどのようにこれを行いますか？

私が言ったように、アイデアは天才に簡単です。 固定サイズm



のビットの配列と、0〜m m - 1



値を生成するk



異なるハッシュ関数のセットm - 1



開始されます。 セットに要素を追加する必要がある場合、各ハッシュ関数の値が要素に対して考慮され、配列内のビットが対応するインデックスで設定されます。



所有権を検証するには、推測して、潜在的なメンバーのハッシュ関数の値を計算し、対応するすべてのビットが1に設定されていることを確認します。これが答えかもしれません。 少なくとも1つのビットが1に等しくない場合、この要素のセットには含まれません-答えは「いいえ」で、要素はフィルタリングされます。

実装

JavaScriptのコード。単純にHabréの場合、多くの人に明らかです。 まず、ビットマップを何らかの形で表現する必要があります。

 function Bits() { var bits = []; function test(index) { return (bits[Math.floor(index / 32)] >>> (index % 32)) & 1; } function set(index) { bits[Math.floor(index / 32)] |= 1 << (index % 32); } return {test: test, set: set}; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また、 k



異なるものをより簡単に作成できるように、パラメーター化されたハッシュ関数のファミリーも必要です。 実装は簡単ですが、驚くほどうまく機能します。

 function Hash() { var seed = Math.floor(Math.random() * 32) + 32; return function (string) { var result = 1; for (var i = 0; i < string.length; ++i) result = (seed * result + string.charCodeAt(i)) & 0xFFFFFFFF; return result; }; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

実は、ブルームフィルター自体：

 function Bloom(size, functions) { var bits = Bits(); function add(string) { for (var i = 0; i < functions.length; ++i) bits.set(functions[i](string) % size); } function test(string) { for (var i = 0; i < functions.length; ++i) if (!bits.test(functions[i](string) % size)) return false; return true; } return {add: add, test: test}; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

使用例：

 var fruits = Bloom(64, [Hash(), Hash()]); fruits.add('apple'); fruits.add('orange'); alert(fruits.test('cabbage') ? ' .' : ' ,  100%.');
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

パラメータ付きのゲームの後、それらにいくつかの最適な値があるはずであることが明らかになります。

最適なパラメーター値

もちろん、私は自分で理論的な最適値を導き出したのではなく、ウィキペディアに行きましたが、それがなくてもロジックをオンにして、いくつかのパターンを推定してキャッチできます。 たとえば、2つの値を格納する場合は大きなビットマップを使用しても意味がありません。逆の場合も同様です。そうしないと、配列が過密になり、誤った回答が「可能」になります。 配列の最適サイズ（ビット単位）：



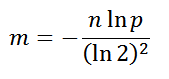
ここで、 n



はフィルターセットに格納されている要素の推定数、 p



は誤検知の望ましい確率です。



ハッシュ関数の数は多くはないはずですが、小さくはなりません。 最適な量：





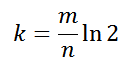
取得した知識を適用します：

 function OptimalBloom(max_members, error_probability) { var size = -(max_members * Math.log(error_probability)) / (Math.LN2 * Math.LN2); var count = (size / max_members) * Math.LN2; size = Math.round(size); count = Math.round(count); var functions = []; for (var i = 0; i < count; ++i) functions[i] = Hash(); return Bloom(size, functions); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

どこで使用しますか？

たとえば、GoogolはBigTableでブルームフィルターを使用してディスクアクセスを削減します。 実際、BigTableは大きくて非常にまばらな多次元テーブルであるため、ほとんどのキーがvoidを指しているため、驚くことではありません。 さらに、データは比較的小さなブロックファイルに分割され、必要なデータが含まれていない場合もありますが、各ファイルは要求時に問い合わせられます。



この場合、RAMをいくらか消費し、ディスク使用量を大幅に削減することが有益です。 負荷を10倍減らすには、キーごとに約5ビットの情報を保存する必要があるとします。 100倍にするには、キーごとに約10ビットが必要です。 独自の結論を導き出します。

さまざまな考え

テストから判断すると、練習用のパラメーターの最適値はやや過大評価されており、1つまたは2つ誤検知のしきい値を安全に下げることができます。 使用するかどうかを必ずテストしてください。おそらく、テストでデータとハッシュ関数のユニークな組み合わせが選択されたか、どこか間違ったことをしました。



明らかに、フィルターから要素を削除することは不可能ですが、これは単純に解決されます-ビットマップをカウンターの配列で置き換えるだけで十分です-追加すると増加し、削除すると減少します。 メモリ消費は当然増加します。



また、フィルターパラメーターを動的に変更できないことも明らかです。 この問題は、フィルターの階層を導入することでエレガントに解決され、後続の各フィルターはより正確になり、必要に応じて階層が深くなります。



おそらくそれだけです。 またね