この記事では、MATLABを例として使用して、結果としてfft(高速フーリエ変換)を生成するものを説明しようとします(おまけとして、この非常に便利な言語で小さな教育プログラムを実施します)。
MATLABを使用すると、不要なオブジェクトを手動で削除する手間を省くことができますが、多かれ少なかれ大量のデータ配列を操作する場合、気まぐれで、メモリ不足について不平を言う習慣があります。 メモリをクリアするには、削除するオブジェクトの名前を指定してクリア手順を使用します。
ここから始めます。 必要なものはすべて自分で生成するので、allキーワードを追加するだけで、アクティブセッション中にワークスペースに蓄積されたすべてのものを安全に削除できます。
clear all%
そのため、まず、モデルの初期データを設定します。 フーリエ解析は、干渉から高調波信号を抽出するのに理想的です。 これを実証するために、特定の定数と異なる周波数と振幅を持つ2つの正弦波の合計を信号として取得します。 ノイズ分散は、最初の正弦波の振幅の3倍です。 また、fftアルゴリズムが計算する周波数帯域の数も設定します。 行末のセミコロンはオプションであり、入力しない場合、関数の計算と変数の設定の結果はコマンドラインに複製され、コードのデバッグに使用できます(ただし、コマンドラインに塗りつぶされたキャンバスを持つ512の値は、特に役立ちません出力にも一定の時間がかかるため、行を閉じることを忘れないことをお勧めします)。
%%
Tm=5;% ()
Fd=512;% ()
Ak=0.5;% ()
A1=1;% ()
A2=0.7;% ()
F1=13;% ()
F2=42;% ()
Phi1=0;% ()
Phi2=37;% ()
An=3*A1;% ()
FftL=1024;%
MATLAB(Matrix Laboratory)は、その名前が示すように、主に配列を操作するために設計されており、そのほとんどすべての計算アルゴリズムはベクトルを操作するために最適化されています。 また、便利な作業ツールが豊富にあるため、目立たないように、マトリックスと同じ数のソースデータを表示するようになっています。 特に、与えられたステップ(この例では1 \ Fd)で増加(減少)量の配列を簡単に生成できます:
%%
T=0:1/Fd:Tm;%
ランダムガウスノイズはrandn関数によって設定され、その結果はパラメーターで指定された次元の配列になります。 一貫性を保つために、時間サンプルの配列の長さに対応する長さを持つ文字列(最初のパラメーター1)として定義します。これは、長さ関数によって計算されます。
Noise=An*randn(1,length(T));%
記号*は、乗算を示すために使用されます。 なぜなら ほとんどの場合、アクションはベクトルに対して実行され、乗算はベクトルによって暗示されますが、この演算子をオーバーロードすることなく、ドットの前にドット(。*)を追加することで要素単位の乗算に使用することも簡単に可能です。 ベクトルにスカラーを乗算する場合、乗算の前のポイントはオプションです。 また、追加されたドットは、要素ごとに増分および除算を行います。
Signal=Ak+A1*sind((F1*360).*T+Phi1)+A2*sind((F2*360).*T+Phi2);% ( 2 )
次に、この記事が考案された目的であるfft()関数に移りましょう。 標準のMATLAB関数の引数は、信号自体(この場合はSignal)、結果ベクトルの次元(FftL)、および測定値です。
最後の引数は、多次元配列が入力された場合に信号が位置する次元を決定します(このパラメーターはフーリエ変換の次元と間違われることがありますが、そうではありません。MATLABには2次元fft2()および多次元fftn()アルゴリズムが実装されていますが) 。 信号はベクトルなので、完全に省略することができます。
まず、ノイズのない信号を検討します。 その結果、複素数のベクトルを取得します。 これは、周波数領域での信号を指数形式で表したものです。 つまり これらの複素数のモジュールは、対応する周波数の振幅を表し(より正確には、周波数帯域は以下を参照)、引数はそれらの初期位相です。 また、得られた位相がラジアンで明確に計算されている場合、振幅と周波数ではそれほど単純ではありません。
たとえば、信号にフーリエ変換を適用し、出力でベクトルの絶対値を取得すると、おおよそ次の図が得られます。
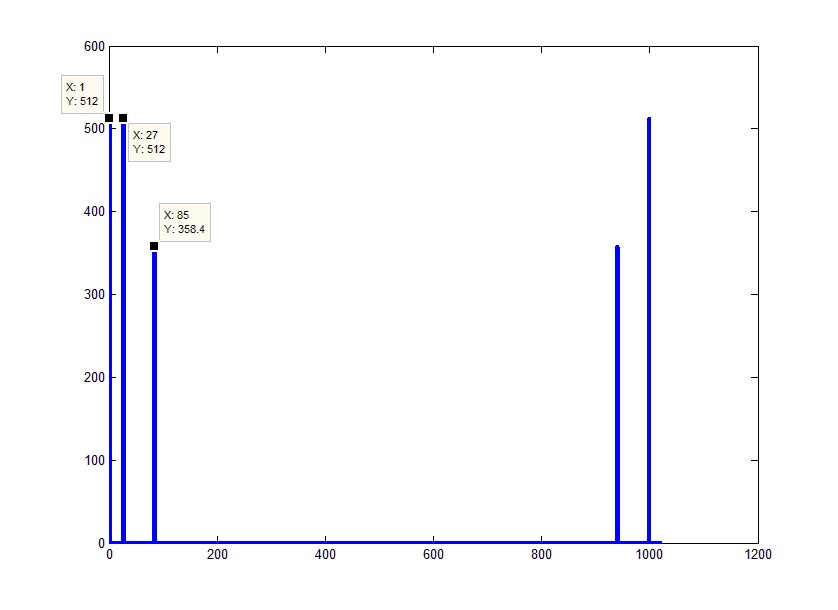
2次元グラフを作成するには、プロット関数を使用すると便利です。 この関数で使用される主なパラメーターは、ポイントの1次元配列です。最初のパラメーターは縦座標軸を設定し、2番目のパラメーターは対応するポイントの関数値を設定します。 1つの配列のみを渡す場合、1の固定ステップで表示されます。
結果の写真をよく見ると、予想とは多少異なることがわかります。 下のグラフでは、予想される3x(定数+ 2正弦波)の代わりに5つのピークがあり、それらの振幅は元の信号の振幅と一致せず、横軸はほとんど周波数を反映していません。
まず、アルゴリズムのスコアは、正の周波数だけでなく負の周波数も選別され、グラフの右側が実際のスペクトルの「ミラー」表示になるように設計されていることを考慮する必要があります。 つまり 実際、0(信号の一定部分に対応)は配列の中央になければなりません。 この状況は、配列の長さの半分だけ循環シフトを行うことで修正できます。 これらの目的のために、MATLABには、最初の要素を配列の中央にシフトするシフト関数fftshift()があります。
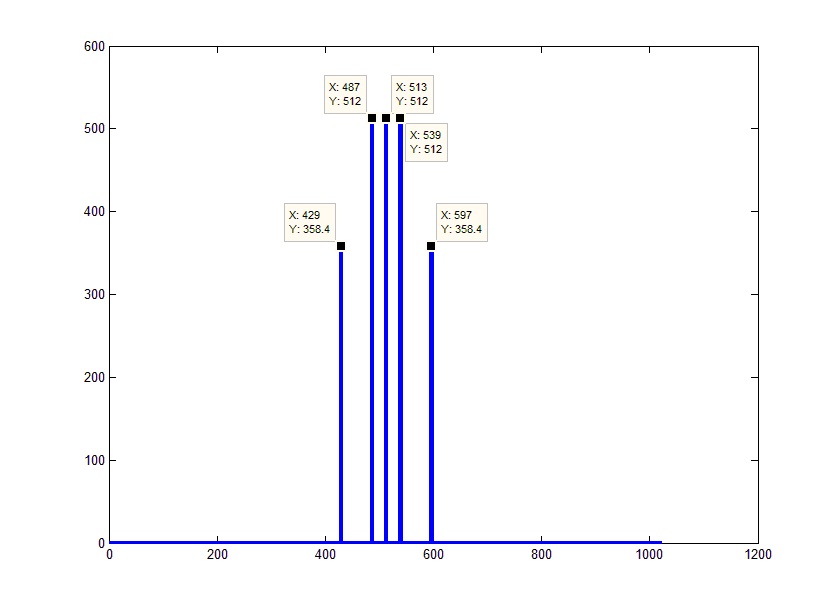
ここで、値の軸に注目しましょう。
サンプリングの定理(ナイキストシャノンの定理またはより愛国的なコテルニコフの定理としても知られています)によると、離散信号のスペクトルはサンプリング周波数(Fd)の半分に制限されます。 または、この例では、左側にFd / 2があり、右側にFd / 2があります。 つまり 結果の配列全体がFd周波数をカバーします。 ここから、配列の長さを知っている(またはパラメーターとしてパラメーターを独立して設定する)ことを考慮して、ステップFd / FftLで値の配列の形式で周波数を取得します(実際には、右端の周波数は1境界より小さくなります)つまり、Fd / 2-Fd / FftL):
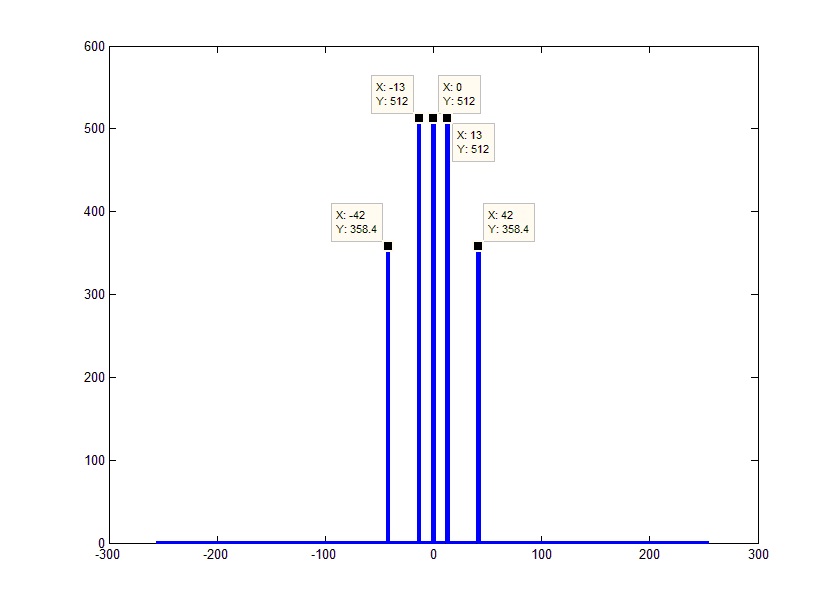
周波数の位相を見ると、対応する負の周波数の負の位相に等しいことがわかります。 スペクトルの左部分と右部分の振幅が等しいこと、およびそれらの位相と符号の対応を考えると、スペクトル全体は振幅が2倍の正の部分と等しくなります。 例外は0エレメントのみで、ミラーの半分はありません。 したがって、「理解できない」多くの場合、不必要な負の周波数を取り除くことができます。 これは、元の配列の末尾を破棄し、残りの要素に2を乗算するだけですぐに実行できます(定数コンポーネントを除く)。
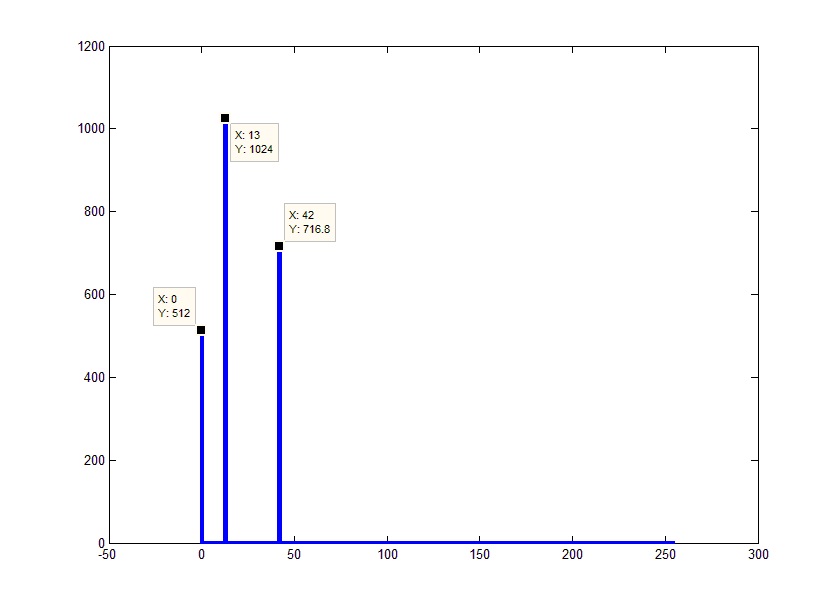
今では、すでに予想される結果に似ています。 気になるのは振幅だけです。 これにより、すべてが非常に簡単です。 なぜなら 高速フーリエ変換は実際には各周波数の変換コア(複素指数)を乗算した信号の合計であるため、実際の結果は正確に合計数(結果としての周波数)で得られる結果よりも小さくなります。 結果は、結果の要素の数で除算する必要があります(結果が、破棄された部分(つまり、指定されたFftL)とともに回答全体であることを忘れないでください):
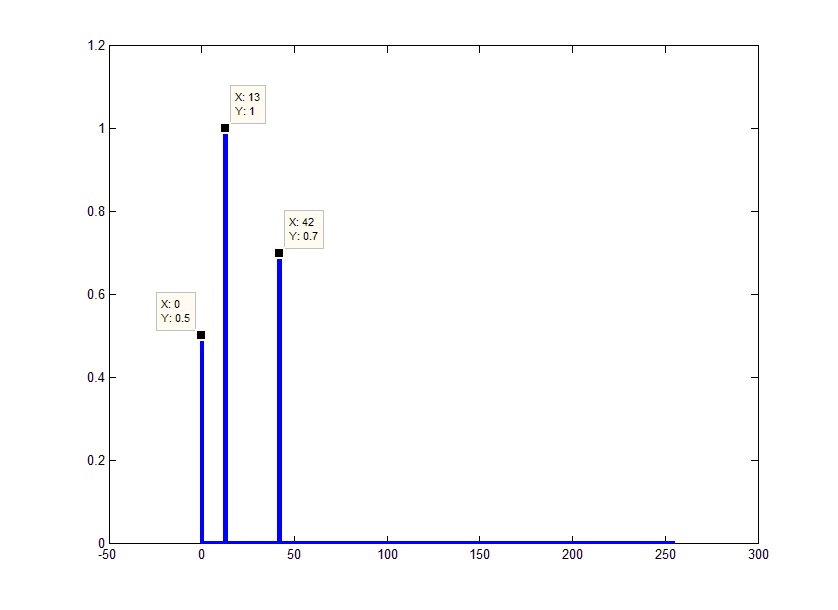
言及する価値のあるもう一つのこと。 スペクトル表現では、アルゴリズムがヒットするのはその周波数での信号値ではなく、周波数がFd / FftLの増分で追従することを計算しますが、帯域内の値(ステップの幅に等しい)です。 つまり 複数のサンプルがこのバンドに分類される場合、それらは合計されます。 たとえば、アルゴリズムの結果として行数を減らすことができます。
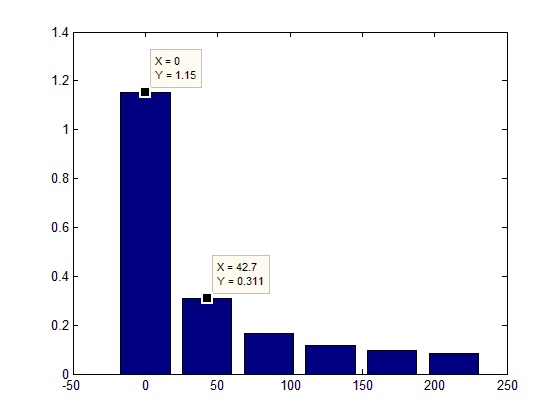
ただし、これは作業の精度を即座に軽率に高める価値があるという意味ではありません。 また、これは否定的な結果につながります。なぜなら、 分解能が信号のサンプリング周波数に匹敵する場合、「ウィンドウ」の高調波はスペクトルに入ります。これは、実際の信号ではなく、その離散表現に関連しています。
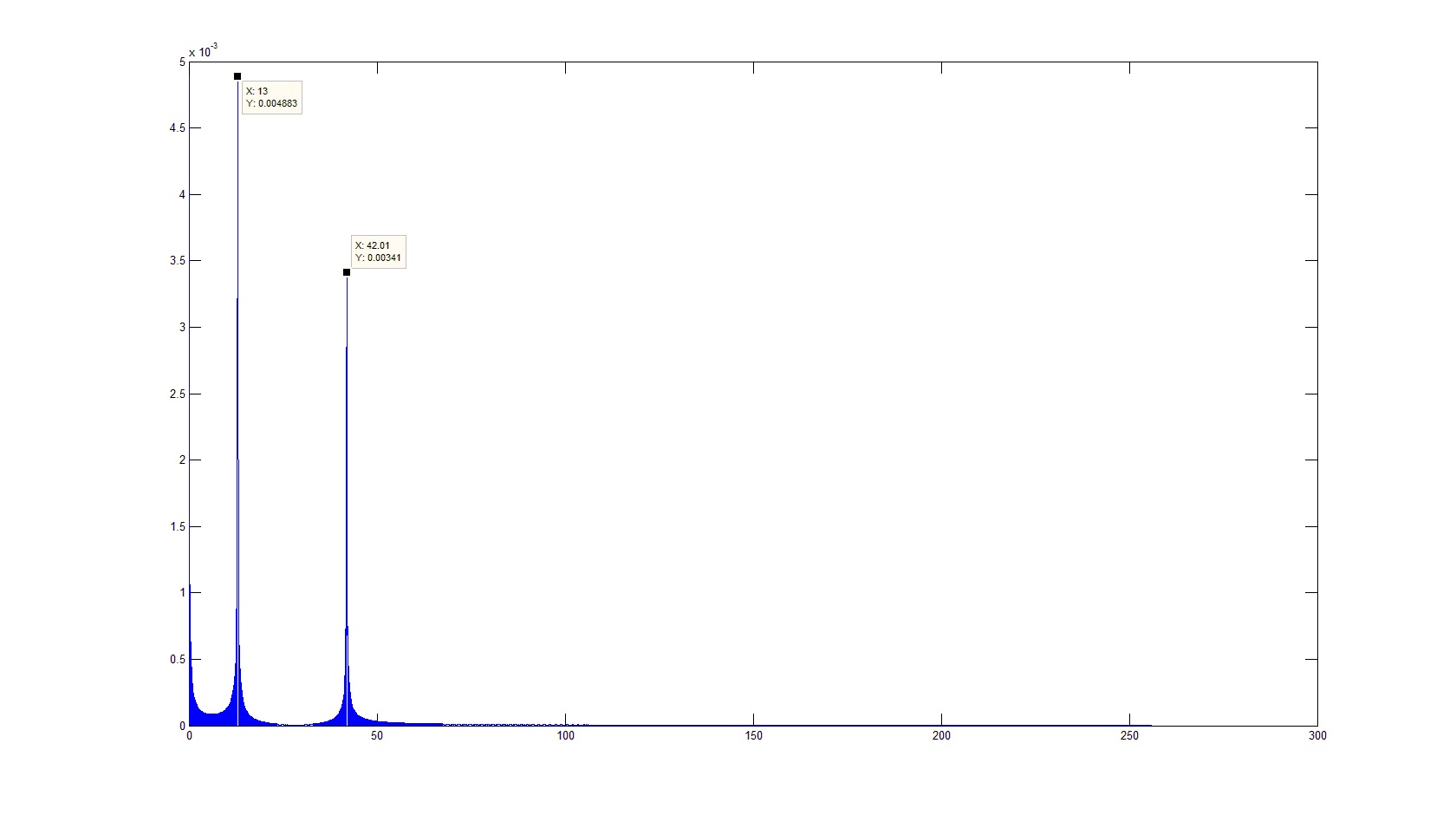
または、いずれかの不一致の近傍。
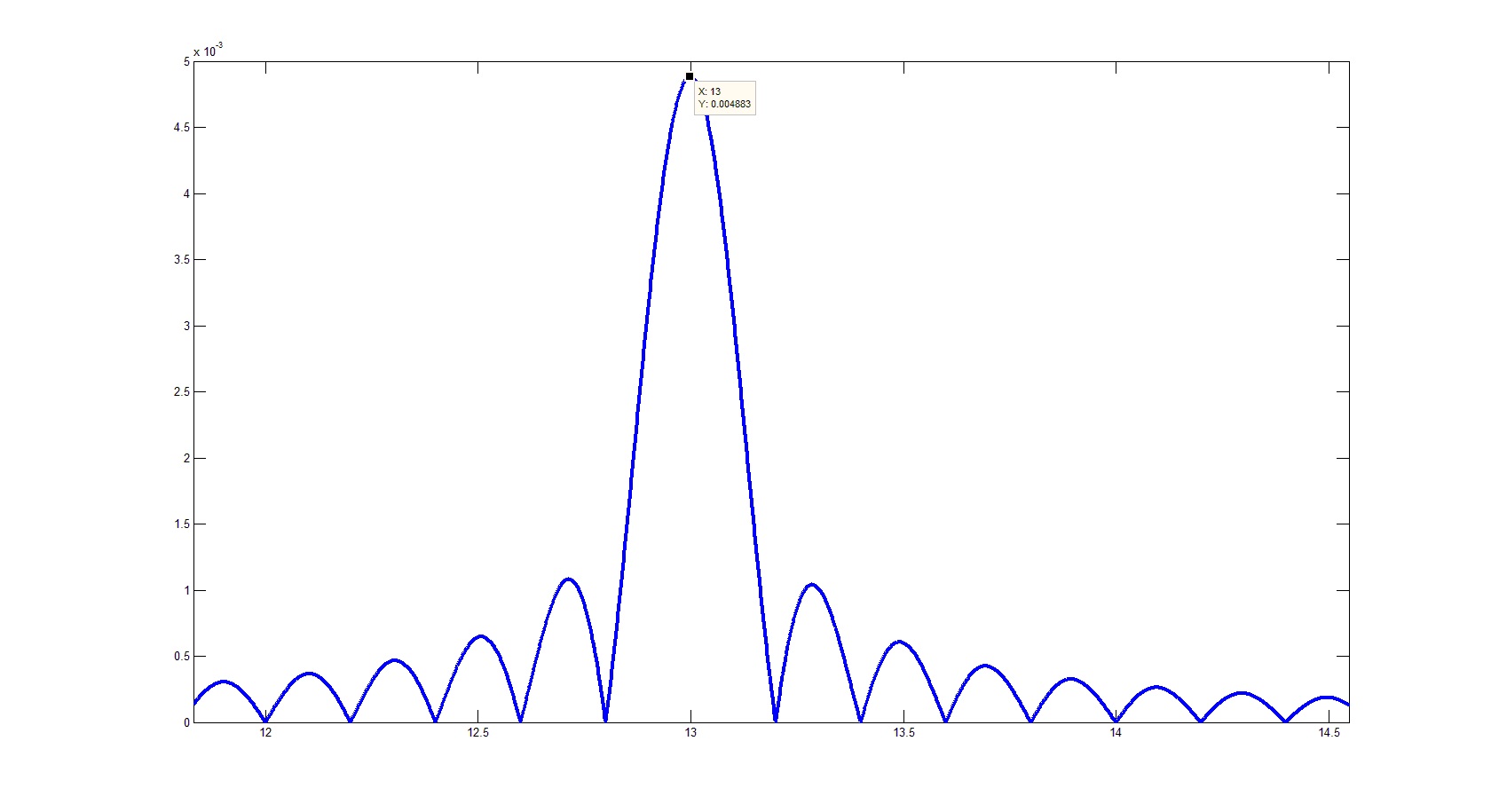
fftを正規化するコードは次のようになります。
%%
FftS=abs(fft(Signal,FftL));%
FftS=2*FftS./FftL;%
FftS(1)=FftS(1)/2;%
FftSh=abs(fft(Signal+Noise,FftL));% +
FftSh=2*FftSh./FftL;%
FftSh(1)=FftSh(1)/2;%
結果を出力するだけです。 サブプロット機能を使用すると、ウィンドウをいくつかの領域に分割してグラフを表示できます。
%%
subplot(2,1,1);%
plot(T,Signal);%
title('');%
xlabel(' ()');%
ylabel(' ()');%
subplot(2,1,2);%
plot(T,Signal+Noise);% +
title('+');%
xlabel(' ()');%
ylabel(' ()');%
F=0:Fd/FftL:Fd/2-1/FftL;%
figure%
subplot(2,1,1);%
plot(F,FftS(1:length(F)));%
title(' ');%
xlabel(' ()');%
ylabel(' ()');%
subplot(2,1,2);%
plot(F,FftSh(1:length(F)));%
title(' ');%
xlabel(' ()');%
ylabel(' ()');%
コード実行の結果は次のようになります。
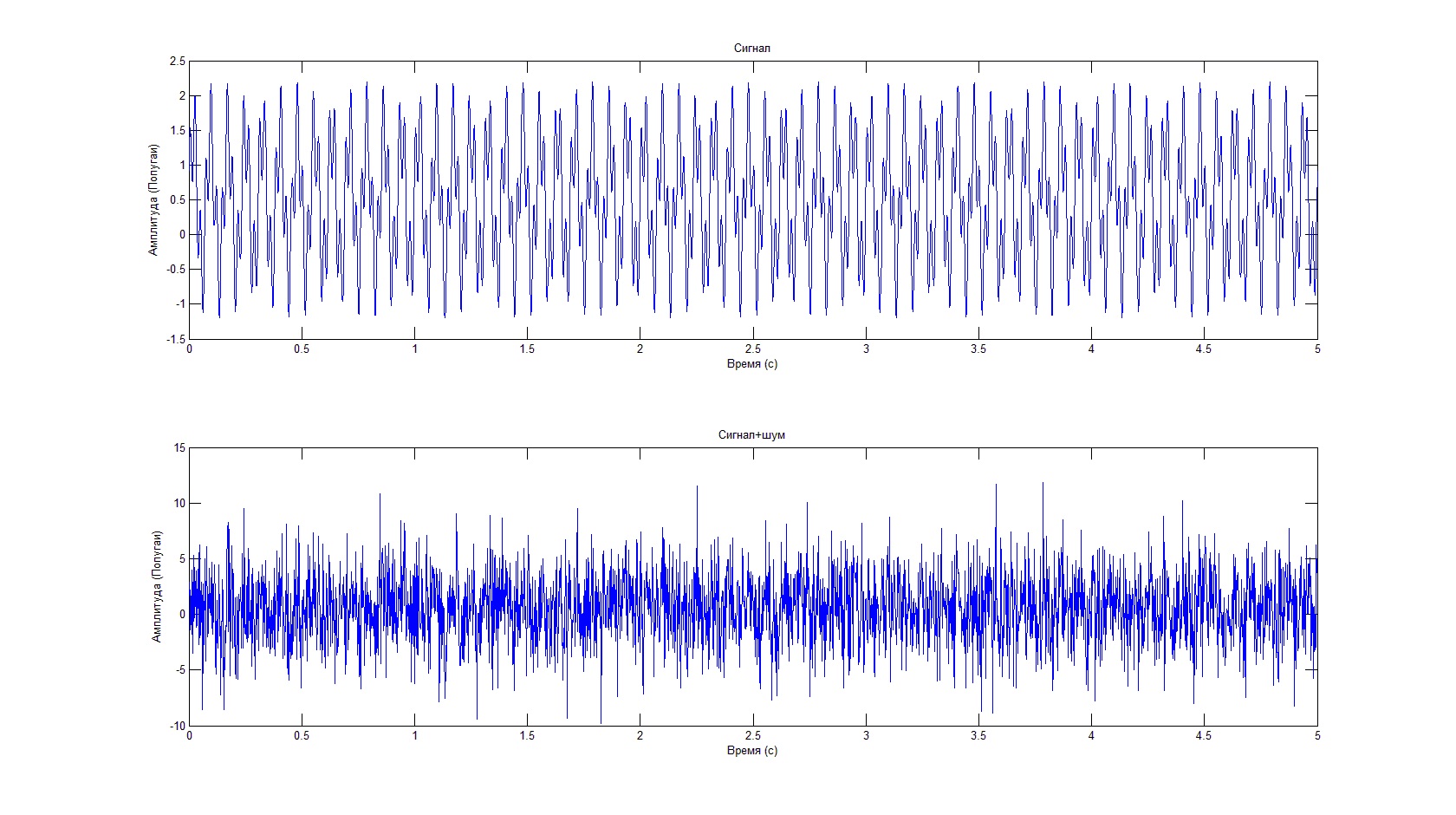
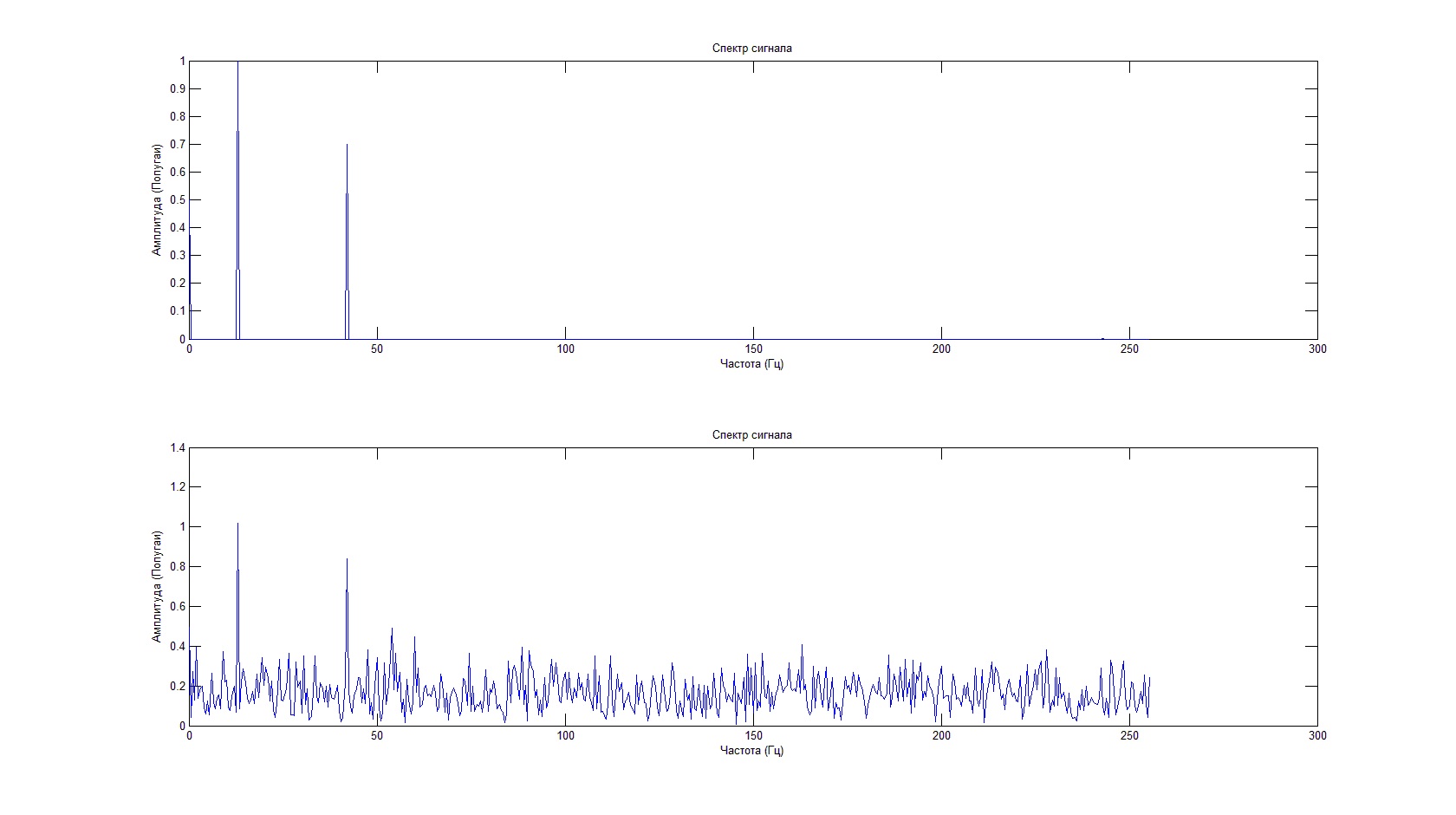
有用な信号はノイズの背景に対して見えないという事実にもかかわらず、スペクトル特性により、周波数と振幅を決定できます。
このテキストがお役に立てば幸いです。